摘要: 材料的基本力学性能,如刚度和强度等,通常是在准静态加载条件下测定的,即加载速度限制在不对结果产生影响的程度,但实际上该条件并没有明显的界限,工程中材料常常处于动态加载情况,其刚度和强度与静态存在明显的区别。不仅如何获得材料的动态性能是一个重要的技术问题,明确低速情况下刚度、强度等材料性能的表现特征,探讨造成材料动态性能与静态性能不同的物理机制也是一个具有理论意义的课题。本文从能量守恒的角度,对材料在动态加载情况下的变形与加载速度的关系进行了分析,基于材料力学性能与加载过程无关的认识,本文研究说明在动态加载情况下,材料变形速度造成材料细观变形机制发生变化,从而影响了材料宏观性能。上述结论与现有文献中的实验结果相比较,二者体现的规律呈现一致性。
Abstract:
The basic mechanical properties of materials, such as stiffness and strength, are usually measured under quasi-static loading conditions, i.e., the loading speed is limited to the extent which does not affect the results, but in fact there is no obvious boundary between the conditions. In engineering, materials are often under dynamic loading, and their stiffness and strength are obviously different from that in static state. Not only how to obtain the dynamic properties of materials is an important technical issue, but also it is of theoretical significance to clarify the performance characteristics of materials such as stiffness and strength at low speed, and to explore the physical mechanism that causes the difference between the dynamic and static properties of materials. From the perspective of energy conservation, this paper analyses the relationship between deformation and loading speed of materials under dynamic loading. Based on the knowledge that mechanical properties of materials are independent of the loading process, this paper shows that under dynamic loading, the deformation speed of materials changes the micro-deformation mechanism of materials, thus affecting the macroscopic properties of materials. The above conclusions are consistent with the experimental results in the existing literature.
1. 引言
材料的力学性能通常指材料刚度和强度,是在实验室中通过准静态加载测量而得的。工程实际中结构常常承受动态载荷,即材料具有较大的应变速率,材料表现出的力学性能与静态情况往往明显不同,实验中动态加载情况下测试材料性能的变化与速度的关系密不可分 [1]。根据工程经验,材料在应变速率较大时其变形程度会相应减小 [2],对于脆性材料而言,其变化可能相对不明显,但对延性材料如各类金属材料则较为明显,因此可以说明动态加载下材料的变形机制变化会影响到材料的宏观动态性能 [3]。
结构在外部力作用下抵抗变形的能力即为刚度,本文做出以下界定:动刚度是指动态加载条件下,材料在线弹性变形范围内应力–应变关系曲线的斜率。材料的杨氏模量是材料的属性(静态),因此动刚度只是体现动态载荷与变形的关系受载荷速率影响,而不一定是反映杨氏模量的真实变化。相应的,动强度反映了动态载荷下材料失效的对应强度,在考虑金属材料时一般可取其屈服强度作为标准,其屈服强度本身也是材料的固有属性(静态),然而动态载荷下其表现出来的数值可能会因载荷速率变化产生变化。
各类材料在动态情况下的力学性能研究以及数值模拟相对较多,例如张诗昌针对镁合金的弹性模量问题从温度与应变率角度进行分析 [4];冯擎峰利用Hopkinson压杆装置对高速冲击下铝合金的变形行为,拟合出对应的高变形速率下Johnson-Cook模型中的参数,明确了应变速率对材料动刚度的影响 [5];杨丽研究了碳钢对于加载速率的动态响应,指出了相应材料动强度的变化 [6]。大量相关实验研究表明,金属材料在不同工况下的力学行为有所不同,在通常的冲击动力学研究中,材料的应变速率可达到103 s−1,以1 m长的试件为例,其相应加载速率可达到1000 m/s,在如此高速的情况下,相应力学性能与静态有明确的区别,研究方法也完全不同 [7] [8] [9];而当速度较低时,如加载速率在1~102 s−1以下时,该过程中基本可以认为满足机械能守恒定律,忽略局部温度升高效果 [5],然而该部分内容以定性分析为主,相关研究也较少。
材料的动态性能与静态性能存在明显差异,对材料动态性能的研究具有重要意义。本文基于能量守恒原理,建立了材料动态力学性能,即动刚度/动强度与加载速度的关系,进而分析了加载速度对材料动态性能的影响。与现有实验数据相比较,本文的分析有助于揭示材料动态力学行为的本质与规律。
2. 考虑加载速率的材料动刚度表达式
基于对于动态加载问题的文献研究以及基本认识,本文提出下述动态加载下的材料力学性能假说:
1) 材料宏观性能是材料细观结构决定的,不因加载过程不同而变化;
2) 在动态加载过程中,材料表现出的力学性能的变化是材料变形速度引起的,而非是反映材料固有属性的变化;
3) 在动态加载过程中,考虑变形速度相对较小的情况,忽略加载过程中的温度变化,则该系统机械能守恒,外力做功转化为材料变形能与材料动能。
由此可知,在动态加载条件下,基于能量守恒原理,材料的名义刚度可表示为材料静刚度与材料动能的函数。为简化分析,建立受压杆模型如图1所示,假设加载过程满足理想动态变形条件,即:
1) 具有稳定的加载速度,即加载端能够保持固定的移动速度;
2) 变形具有一致性,即无变形的弹性回波。

Figure 1. Diagram of specimen and loading
图1. 试件及加载示意图
如图1所示,L0为试件原始长度,载荷为P,V0为加载速度,即加载面的速度,为一定值。假设试件中任一点在VOx系中的速度可表示为
 (1)
(1)
其中t为时间,由于材料质量不变,即
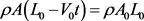 (2)
(2)
因此,试件的动能WV为
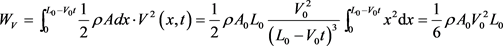 (3)
(3)
式(3)中,A为受压杆变形时的截面积,A0为受压杆未变形时的初始截面积。设试件上某点x,其速度为V(x,t),在Δt时刻后,点x发生位移V(x,t)Δt,点x + Δx发生位移V(x + Δx, t) Δt,因此点x的应变可表示为
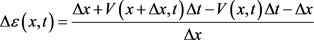 (4)
(4)
将式(1)代入上式,并令Δx、Δt趋于零,有
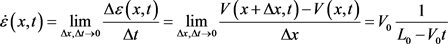 (5)
(5)
上式对时间t积分,有
 (6)
(6)
因此,试件的应变能Wε为
 (7)
(7)
试件的加载面保持恒定变形速度,则相应的,外载荷是随时间变化的。在加载过程中,外载做功W为
 (8)
(8)
根据能量守恒,对图1所示系统,有
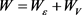 (9)
(9)
亦即
 (9*)
(9*)
将式(3),式(7)和式(8)带入式(9*),有
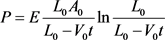 (10)
(10)
试件(宏观)名义应力 可表示为
可表示为
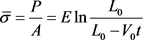 (11)
(11)
参照式(6),试件的应变处处相等,因此可知(宏观)总应变,亦即试件的名义应变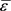 等于真实应变,即为
等于真实应变,即为
 (12)
(12)
因此动刚度表达式为:
 (13)
(13)
根据式(13)可知,金属材料的动态刚度等于准静态下的弹性模量,该结论是基于机械能守恒以及无局部材料密度变化的前提下得出的,在变形速度较低的情况下成立,与图2中的低速段实验数据相一致。
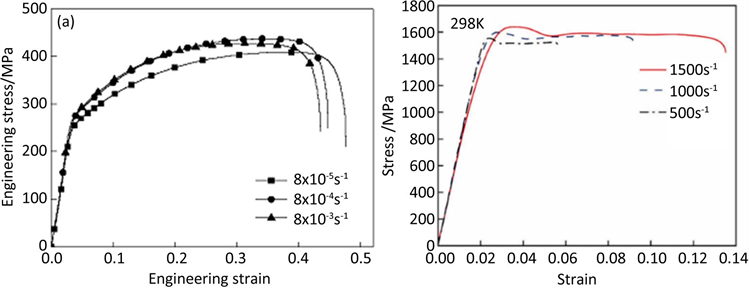
Figure 2. Engineering stress-strain curve of Invar 36 (left) and TC18 (right)
图2. Invar 36合金(左)和TC18(右)的工程应力–应变曲线 [3]
3. 考虑加载速率的材料动强度分析
材料强度与材料的类型、加载速率以及材质不均匀程度等因素有关,岩石、混凝土类脆性材料在动态加载下的强度差异主要是由材料的不均匀性造成的,其强度表现出较强的随机性。相比之下,金属材料的动强度规律较为一致,其加载屈服前必然产生一定的塑性变形,若加载速度较大,则塑性变性滑移面不利于向外载荷方向转动,相当于增加滑移面的阻力,同时形变硬化得不到回复过程,使得继续塑性应变的阻力增大,在宏观上表现为屈服强度增高。因此,从屈服强度的角度分析,加载速度会对金属材料屈服强度产生正向影响,即某种程度上提高材料的动强度。
该结论在现有的研究结果中可得到证实,如孙伶俐 [10] 从0.002/s至0.1/s的应变增加速率测试316不锈钢的屈服强度,随着加载速率增大,屈服强度比从0.3增大至0.36,在慢速情况下能够获得接近于屈服强度标准值的结果,而大速度情况下的屈服强度是明显增大的。
4. 总结
本文基于能量守恒原理,建立了材料动刚度、动强度与加载速度的关系,通过相关的实验数据分析了加载速度对材料动态性能的影响,可分为以下几点:
1) 在高应变速率(>103 s−1)下,材料的动态性能研究表明,动态载荷下的材料性能与静态性能存在巨大差异,这一认识与冲击动力学的分析结果一致;
2) 在应变速率相对较低的情况(1~102 s−1)下,材料的加载速率明显低于典型冲击速率,但远高于准静态加载速率,在此条件下,材料不出现局部大变形以及相应的温度变化,即机械能守恒,本文通过理论分析推导可得此时材料动刚度的大小与准静态下一致;
3) 虽然在应变速率1~102 s−1范围内材料动刚度基本不发生变化,但材料的动强度与应变速率变化有紧密关系。对于金属材料,应变速率越大,则其限制塑性变形的情况越明显,相应的动强度则会越高。该结论在整个应变速率变化范围内均有所体现,且相比于准静态的材料强度,通常情况下其动强度增幅比较小。