1. 绪论
5G时代,万物互联不再是空话。高达TB级的传输速率和海量节点数,为智能生产生活赋予了强大的助推力。未来,空间里将覆盖着密集的传感器网络,对信息的把控将更为彻底。许多情况下,并不需要了解每一个传感器的数据,更想获取的是区域内的总体指标参数,简化决策,实时找到故障区域。为解决这一问题,多传感器的信息融合技术正在被众多学者研究 [1]。但其相关技术、算法,都有一定的局限性和缺陷。所以,还需要进一步的探索,为5G时代传感器的改革创新铺设通畅的道路。
多传感器信息融合(Multi-sensor Information Fusion, MSIF),是利用计算机技术将来自多个传感源的信息和数据,在一定准则下加以自动分析和综合的信息处理过程。具体流程如图1所示。

Figure 1. Multi-sensor information fusion process
图1. 多传感器信息融合流程
目前,主流的多传感器信息融合技术主要分为三类 [3]。第一类为先验知识型,以加权平均法为代表;第二类为概率分配型,包括卡尔曼滤波法、D-S证据理论;第三类为训练学习型,例如模糊逻辑控制、专家系统、人工神经网络法等 [2]。各类算法的介绍如下:(1) 加权平均法 [4]:对多个传感器的数据进行加权、平均、累加等算术操作,最终得到一个统一的指标。该方法操作简单、计算迅速、复杂程度低,但需预先获取各个传感器的加权值。合理精确的加权值难以获取且随时间、数据变化的关系不明确,固定的加权值可能会造成较大的误差。(2) 概率论方法 [5]:对多个传感器的数据进行统计分析、去量纲化、剔除奇点等操作,利用概率论方法,结合先验知识等。最终得到统一的指标。这种方法理论依据充足、响应快速,但需先验知识,对于黑盒类型系统不适用。(3) D-S证据理论 [6]:无需先验知识,而是使用基本的概论分配函数代入合成公式中,进行信息融合,是处理不确定问题的通用框架。但是随着信息规模、类型的不断扩大,计算时间成几何倍数的增长,实时性差,不利于实时性的决策。
实际在进行多传感器信息融合的过程中,出现了许多的问题和难点。具体如下:
(1) 数据固有缺陷:不和谐数据奇点、偶然误码。
(2) 量纲和维度:量纲、维数不统一。
(3) 数据关联:正负性指标需分别处理、数据类型多。
针对现有主流多传感器信息融合技术在适用范围、系统适应度、先验知识依赖强等缺陷 [1],本文设计了一种基于投影寻踪和模拟退火法的多传感器信息融合算法来改善解决这些问题。第2部分对该算法进行详细的描述,并对算法进行逐块的介绍和分析讨论。第3部分给出了该算法测试结果,并将该结果与实际数据对比,与在未融合信息的传感器数据进行对比。第4部分对本研究工作进行了总结与讨论。
2. 方法
2.1. 前人的方法及改进流程
前人运用了多种类型的算法来解决多传感器信息融合的问题。主要有(1):D-S证据理论,传统的D-S证据理论框架为利用有限个基本概率分配函数
,来构造一个辨识框架,从而进行系统辨识,给出一个综合指标。D-S证据的理论合成公式:
(2) 加权平均法,加权平均法基本原理是观察大量样本,取平均权值作为经验权值,将各个样本数值与权值进行累积求和。基本公式为
,其中
为样本j的第i个指标的经验权值,
为第j个样本值。(3)概率论方法,概率论法是基于频率和权数的转化方法,在加权平均法基础上进一步作出的改进。研究的思想是某一类信息数据对系统出现较大影响频率作为该类型信息的权重划分依据。基本公式如下:
本算法设计基于前人的基础进行了改进,改进的流程和具体内容如图2所示。
改进后的算法具体流程如图3所示。
2.2. 统一量纲化及正负性指标处理
统一量纲化及正负性指标处理的原理
实际的生产生活问题中,传感器数据类型丰富。如温度、湿度、压力、ph值、光照等等。针对某一项指标,方便统计,但如果要求根据多个指标给环境或状态一个综合的评估值,可能比较困难。人们借自身知觉或经验进行直接的感受评估,但机器没有这种机能。将各种类型丰富的数据去量纲化,只保留本质的特征因子,会便于机器的准确计算和决策。对于有些类型的数据值,希望越大越好,而有些数据值,却希望越小越好。这即是正负指标的问题。因此要解决量纲去除的同时还要考虑到正负指标的处理。本文采用的数据处理方法如下:

Figure 2. Multi-sensor information fusion algorithm to improve the process
图2. 多传感器信息融合算法改进流程

Figure 3. Overall flow chart of fusion algorithm
图3. 融合算法总体流程图
定义某类型数据为
,
为第j列指标的最大值,
为第j列的最小值。对于正向性指标,做如下处理:
对于负向性指标,做如下处理:
2.3. 投影寻踪法原理及应用
2.3.1. 投影方向的设计
对于未知系统,没有先验经验,或者系统为非线性、时变的。投影方向的选择往往也是时变的随机的,或者是遵循某一规则的混沌的。需要从不同的方向去观察数据 [7] [8],找到最能充分挖掘数据特征的最优投影方向。设m维单位向量,即各指标的投影方向向量,第i个样本在一维线性空间的投影特征值
的表达式为:
为构造m维单位投影向量a,设计了随机函数Rand_Value,用以产生满足上述规则的
。另一方面,也是为了适应黑盒型系统。使得融合算法有更好的适应性,同时解决了固定权值的不灵活性。增强了系统的弹性度和自适应度。
2.3.2. 投影方向优良评估设计
一个优良的评估值集合,应当满足概率论高斯分布的基本规则。即优、差的评估值所占比例较小,中等的评估值所占比例较大。因此在评估最优投影方向的规则设计上,要求投影值
的分布特征满足局部投影点尽可能密集,凝聚成若干点团。而整体上的投影点团尽可能的散开 [7]。为此,构造投影指标函数:
其中
为投影值
的标准差,
为投影值
的局部密度。这里选出密度窗口半径为0.1倍的
。对
内的元素进行半径穷举窗口比较,半径小于窗口值
则通过,送入评估值累加器,否则不进行累加。最终得到的值即是对一个投影向量优良评估的值 [9]。采用的思想为聚类K-MEANS [10],鉴于实际的系统状态总是在局部稳定和全区分散的实际情况,投影方向的评估规则也是根据是否符合高斯概率分布和聚类离散特征进行设计的。评估投向方向优良性的具体流程如图4所示。
2.4. 模拟退火法原理及应用
2.4.1. 模拟退火法的原理
模拟退火法是从物理退火中得到启发,从而设计出的最优化算法。粒子在某个温度T时,固体所处的状态具有一定的随机性,而这些状态之间的转换能否实现由Metropolis准则决定 [11]。Metropoils准则定义了物体在某一温度T下从状态i转移到状态j的概率P,其公式如下:
上式中e为自然对数,E(i)和E(j)分别表示物体在状态i与状态j下的内能,
表示内能的增量,K是玻尔兹曼常数。

Figure 4. Projection direction good evaluation flowchart
图4. 投影方向优良评估流程图
2.4.2. 模拟退火法在本文中的应用
本文对模拟退火法的应用是对投影向量
按照一定的准则生成一个评判
优良的标量
,进行模拟退火,与新的
生成的标量
进行比较。如果
,则接受新的变化
。否则如果
(这里的
指的是0~1内的随机数),那么也接受新的变化。否则不会接受新的变化。在冷却过程中,冷却反弹的几率,即在
情况下仍然接受新变化的几率,会随着温度的下降逐渐下降,即温度越低就越稳定的退火原理。所以迭代过程中概率反弹会越来越小,这也符合自然降温或优胜劣汰的生存规律。最终,冷却结束,保留的即是最优的投影方向。选取的测试集迭代大约45,900次时得到最优解。
2.4.3. 模拟退火法流程
根据以上原理进行退火算法设计,流程如图5所示。
3. 结果
本文采取的算法测试集为Kaggle数据库中一农业养殖大棚中6种传感器所测得的100组样本数据(土壤含水率传感器、温度传感器、湿度传感器、光照强度传感器、二氧化碳传感器、土壤ph值传感器)部分样本数据如表1所示。
经过信息融合后得到的样本综合评估值如图6所示,100组样本产生的多传感器信息融合的综合评估值随机分布,而且中部的评估值较为集中。对得到的投影向量进行散点图分析,该数据的分布满足K-MEANS聚类和概率论的原则。多传感器信息融合得到的综合指标散点分布图如图7所示,可以明显的发现局部的点聚集成团,而整体又尽可能的散开。

Figure 6. Sample comprehensive evaluation value
图6. 样本综合评估值

Figure 7. Sample comprehensive evaluation scatter distribution
图7. 样本综合评估散点分布图
回归到原始的表格数据,这里我们观察评分最高点样本、最低点样本、平均点样本。图中最高点样本、最低点样本、平均点样本编号为86、22、42。
86号样本数据:
22号样本数据:
42号样本数据:
数据从左至右分别为土壤含水率、二氧化碳浓度、光照强度、最适温度偏差、最适湿度偏差、最适土壤ph值偏差。前三项为正向指标,而后三项为负相关指标。经过信息融合评分值最高的样本的土壤含水率、二氧化碳浓度、光照强度均较高,最适温度偏差、最适湿度偏差、最适土壤ph值偏差均较低。虽然在ph值数据上低于平均的水平,但是考虑总体上的信息融合是综合各项指标,对于所得出的结果仍是可信的。
对于非融合的单一传感器数据,传统的做法是将各项数据逐一传送进行各类数据的阈值判断。传统的非融合单一传感器数据采集与决策模式,如图8所示。
不考虑传感器故障的情况下,分布式的单一传感器网络,在不进行信息融合的情况下,很难对于系统有一个全局性的把握。特别是对于复杂、庞大的传感器系统,单一的逐次处理可能会造成控制时机的丧失和资源的浪费以及数据的冗余。下面以一些数据图表进行简要的说明:
图9中,数据庞多且种类很多,还可能包含正负指标不一样的数据类型。如果仍使用传统的非融合单一传感器信息技术处理就很难得到系统整体的情况,大批数据的逐次处理对于系统资源的浪费和对后续系统的扩展不利。而采用多传感器信息融合算法所得到的结果更加清晰简明,有利于决策。
对于非融合单一传感器,假设初始系统的处理复杂度为
,规定每次的系统更新扩展会使得系统在原来的基础上增大为1.13倍的复杂度。第一次更新后系统的复杂度为
,第二次更新后系统的复杂度为
,第三次……计算多次发现系统将会承受几十倍原来复杂度。现假设使用多传感器信息融合技术的系统初始复杂度为
,第k次的复杂度为
。传感器数据融合技术将复杂度为
的系统降低至1/2,同时增添0.001倍的
总体数据指标处理复杂度。得到的系统复杂程度发展特性图如图10所示。从图10可看出经过融合后的计算复杂度在系统不断发展后,所减少的复杂度由3%升高至15%。
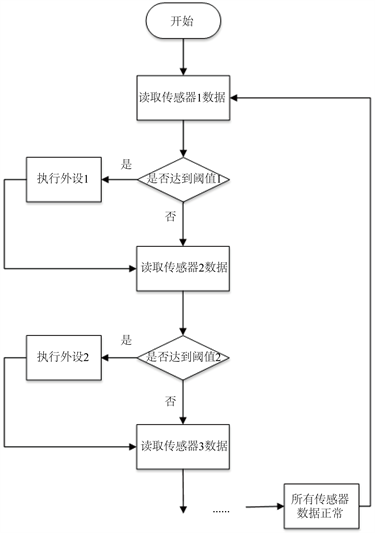
Figure 8. Traditional non-fusion single sensor data acquisition and decision-making mode
图8. 传统的非融合单一传感器数据采集与决策模式

Figure 9. Data graph of multiple sensors
图9. 多个传感器的数据图表

Figure 10. The development chart of system complexity using fusion technology and non- fusion technology
图10. 采用融合技术与非融合技术系统复杂度发展对比图
在本文所选取的测试集指标为6个,组数100,前3项指标为正性指标,后3项为负性指标。算法给出的评估值符合正态分布,样本评估值分布如图7所示。经过回归元数据表中查对正负峰值(样本86、22)、平均值(样本42)。发现峰值综合正向指标和为1047接近各样本正性数据抽取最大值之和1194.568;峰值综合负向指标和为−6.55,接近各样本负性数据抽取最大值之和−1.955。综合评分最低的样本正性指标和为481.054,接近各样本正性数据抽取最小值之和352.857;负性指标和为−43.46,接近各样本负性数据抽取最小值之和−52.641。另外,通过系统聚类窗口半径的调整可以改变系统状态的分层等级;通过改变模拟退火迭代器的迭代次数可以在精准度和实时性之间进行有效的平衡;通过改变反弹机会的窗口步距可以改变系统自然状态奇点对于评估值的影响。综上,本设计可以给多传感器信息融合系统更大的灵活性、适应性。
4. 结论与讨论
本文利用投影寻踪法和模拟退火法结合,吸收了加权平均算法的权值判别、概率分布型算法的概论权值和随机概论向量、神经网络渐缩迭代方法及Sigmod数据统一方法,设计了一种基于加权平均法的多传感器信息融合算法。在加权算法的基础上进行了优化扩展。经过样本测试集的测试,发现算法的计算复杂度较单一传感器信息算法提升了41.6%左右,测试结果的峰值与测试集个样本抽取最大最小峰值基本吻合,有着较优异评估的结果。该算法模型适用范围广,对于正负性指标杂糅和黑盒型系统有专门的处理,结构简洁灵活,可扩展性强。但有的地方还需进一步的改进,比如在算法运算速度和与经验知识结合处理方面,有待提升。
5G时代,万物互联。多传感器信息融合技术给空间传感器网络带来智能化的监控管理。对于多传感器信息融合技术的算法研究将持续进行。随着智能传感技术的不断发展和融合技术的不断完善,人们对于系统或者设备的整体状态的把握将更加精确。智能生活,万物互联的未来已然来临。
基金项目
国家自然科学基金(11703009) (针对平移误差检测的电容式边缘传感器改进研究)。
NOTES
*通讯作者。