1. 引言
转子–轴承系统是旋转机械中最关键的部分,而在设计和运转过程中,能够保证大型旋转机械中转子的稳定性和实用性是至关重要的,随着旋转机械向高效率、高标准发展,研究了不对称双圆盘转子–轴承系统在油膜力下的非线性耦合动力学行为。分析了非解析径向椭圆转子–轴承系统的稳定性和分岔,在稳定性分析中,运用打靶法和轨迹预测跟踪算法研究了系统线性不平衡响应。文献考虑了参数随机分布特性的转子动力学与可靠性 [1] [2] [3]。本节主要分析一个随机参数激励下四维高速转子系统的非线性随机稳定性及随机Hopf分岔。
2. 模型的建立
考虑一个带有广义非线性阻尼的转子模型 [4] [5]。
其中
表示非线性阻尼系数,
是转子系统的固有频率。
和
表示非线性阻尼器的耗散效应,若
,则系统的状态方程变成一个阻尼系数为
的形式,如果
很小的情况下方程的近似解可以采用多种摄动方法得到,由于转子的质量相当大,所以
的值可以被看作很小。
令
,所以方程可以表示为:
考虑到外部的随机因素及其内部材质的不均质性,将系统收到的所有随机因素用Gauss色噪声代替,即
,
其统计性质满足以下条件:
,
,
其中,D和
分别表示噪声强度和关联时间 [6]。
由于色噪声激励下的模型不是Markov过程,因此该模型的随机动力学行为的分析比较困难。本节将利用统一色噪声近似原理将模型简化成一个便于讨论的Gauss白噪声激励下的等效非线性模型。
2.1. 下面将色噪声模型进行等效白化 [6]
根据统一色噪声近似原理,色噪声激励下的模型可以由如下的白噪声激励下的方程组近似表示:
其中,
是Gauss白噪声,满足
,
,
。
为了后续计算方便,这里需要将方程组表示成一阶微分方程组的形式。故令
,可以得到
其中,
表示广义的位移,
表示广义的动量,
。
令
,
,
,
则方程组中(2)(4)式可以表示为
,
将上式关于t求导,消去
可得:
其中
,
,
应用统一色噪声近似方法,令
,进行绝热消去,得到
,其中
,
,
故上式可以改写为
由于
的非线性函数
,
位于模型第2、4个方程的分母上,致使白化模型是一个关于
的强非线性模型,因而很难得到模型的最大Lyapunov指数解析表达式。此处考虑将模型部分线性化,得到一个等效非线性经济周期模型,从而降低模型的非线性强度和复杂性。
白化模型的等效非线性近似,可以得到模型的部分线性化等效近似表达式
记模型第2、4个方程与上述模型第2、4个方程的差为
,则
可以表示为
接着令
的均值为零(
值为零的白噪声),得
由于
不可能恒为零,所以
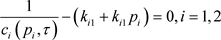
整理上式,得
考虑到在
的邻域,
,
与
是零的高阶无穷小量,因此可以近似的认为上式等效于
即
求解上式,得
最后,代入原模型,得到该模型的等效非线性表达式为:
其中
,
,
,
。
该系统方程的哈密顿函数表示为:
根据拟不可积哈密顿函数
依概率1弱收敛与一个Itô随机扩散过程,则哈密顿函数的平均Itô随机微分方程 [8] 可以表示为:
其中
是标准维纳过程,
和
是随机伊藤方程的漂移和扩散系数,根据随机平均原理:
由于高维系统在运用随机平均原理 [7] [8] 时需要多重积分,所以这里引入极坐标变换来计算漂移和扩散系数。
令
,
则方程转化为:
式中
而
是下列方程之解:
2.2. 接下来主要讨论随机稳定性 [8]
由于
,故当
时,平均Itô随机微分方程的线性化形式为
其中
接着可以得到,当
时,
和
的渐进形式
,
基于Oseledec乘积遍历性定理 [8],可以得到模型的最大Lyapunov指数为:
系统平凡解保持局部渐近稳定的充要条件为:
,即
3. 随机分岔分析
由Itô随机微分方程解得相应的FPK方程为:
式中
因为当
时,
,
,所以根据边界类别原理可得,左边界
属于第一类奇异边界,进而可以得到漂移指数
和扩散指数
,以及特征标值
,
,
则平稳概率密度函数为:
因此可得联合概率密度函数为:
4. 数值模拟
下面主要分析随机Hopf分岔,通过模拟平稳概率密度函数
和联合概率密度函数
的图像随着参数变化而变化。选定
作为分岔参数,然后令
,
,
,
,
,
。为了能够模拟联合概率密度函数,同样令
。
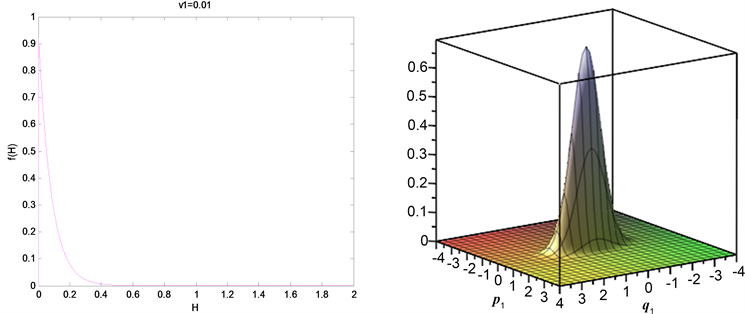
Figure 1. When
,
system stationary probability density function and joint probability density function
图1. 当
时,
系统平稳概率密度函数和联合概率密度函数

Figure 2. When
,
system stationary probability density function and joint probability density function
图2. 当
时,
系统平稳概率密度函数和联合概率密度函数

Figure 3. When
,
system stationary probability density function and joint probability density function
图3. 当
时,
系统平稳概率密度函数和联合概率密度函数
平稳概率密度函数与联合概率密度函数图像如图1~3所示,当参数
在−9.89附近变化时,平稳概率密度图像从单调递减变为单峰状函数,系统发生Hopf分岔;而联合概率密度函数则随着的逐渐变大由单峰状函数变为火山口状,系统发生Hopf分岔。
5. 小结
在本文中,分析了一个非线性阻尼转子系统的随机稳定性及Hopf分岔。首先在一个四维转子–轴承系统中考虑了随机高斯色噪声,然后将高斯色噪声进行白化,再运用哈密顿系统理论对模型进行稳定性分析。在随机平均的过程中引入了极坐标变换,得到了伊藤随机微分方程的漂移系数和扩散系数,通过最大李雅普诺夫指数法,计算出该系统的稳定性条件;最后研究了系统随机Hopf分岔行为。在数值时,只考虑其中2个变量,另外2个变量令为参数的形式,得到联合概率密度函数和平稳概率密度函数随着分分岔参数变化的图像,得以验证得到的理论。