相对论物质波及其对超导电性的解释：基于平等性原理

Relativistic Matter Wave and Its Explanation to Superconductivity: Based on the Equality Principle

摘要: 相对论物质波为超导体中的量子强关联体系的研究提供了一个基本概念。本文通过研究电子碰撞过程中相对论物质波的相位变化，推导出了强关联电子体系的相互作用公式，并对其在超导体中的有效性进行了检验。我们对超导能隙的计算与典型的21种超导体的实验结果吻合得很好。此外，这个相互作用公式清楚地表明，在极低温度下，某些电子与晶格的碰撞将变得既无能量增益又无能量损失，从而为超导机制的研究提供了新的思路。另外，我们提出，相对论物质波是建立在平等性原理基础上的基本概念，从而使得我们的超导理论有更加扎实的理论基础。

Abstract: Relativistic matter waves provide a basic concept for the study of quantum strongly correlated systems in superconductors. In this paper, by studying the phase change of relativistic matter wave in the process of electron collision, the interaction formula of strongly correlated electron system is derived, and its validity in superconductor is checked. Our calculation of energy gap agrees well with experiments for 21 typical superconductors. Moreover, this formula clearly indicates that some electrons colliding with crystal lattice will become no gain and no loss in energy at extremely low temperatures. It provides a new way to study the mechanism of superconductivity. In addition, we put forward that relativistic matter wave is a basic concept based on the equality principle, which makes our superconductivity theory have a more solid theoretical foundation.

1. 引言

在1911年，荷兰科学家H. K. Onnes等人发现汞在极低的温度下其电阻消失，呈现超导状态，从此，超导体的研究受到广泛关注。一方面，多种具有实用潜力的超导材料被发现，另一方面，对超导机理的研究也有很大进展 [1] [2]。人们为阐明超导体的机理做了很多努力 [3] [4] [5] [6]，科学家提出了多种理论，其中比较重要的理论有BCS理论、GL理论。但BCS理论无法解释第二类超导体存在的原因，尤其是根据BCS理论得出的麦克米兰极限温度(超导体的临界转变温度不能高于40 K)，早已被第二类超导体突破。

相对论物质波为超导体中的量子强关联体系的研究提供了一个基本概念 [7]。本文通过研究电子碰撞过程中相对论物质波的相位变化，推导出了强关联电子体系的相互作用公式，并对其在超导体中的有效性进行了检验。我们对超导能隙的计算与典型的21种超导体的实验结果吻合得很好。此外，这个相互作用公式清楚地表明，在极低温度下，某些电子与晶格的碰撞将变得既无能量增益又无能量损失，从而为超导机制的研究提供了新的思路。另外，我们提出，相对论物质波是建立在平等性原理基础上的基本概念，从而使得我们的超导理论有更加扎实的理论基础。

2. 粒子碰撞中的相对论物质波

在电磁矢势A中，考虑一个粒子，它的物质波的积分形式与动量算符形式是一一对应的：

$\varphi =\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x\left(m{u}_{\mu }+q{A}_{\mu }\right)\text{d}{x}_{\mu }}\right)\iff {\hat{p}}_{\mu }\equiv -i\hslash \frac{\partial }{\partial x_{\mu }}-q{A}_{\mu }$ . (1)

这个式子就是相对论物质波的定义 [7]，这里m是电荷为q的粒子质量， $u_{\mu }$ 是粒子的四维速度， $A_{\mu }$ 是电磁四维矢势， $\mu =\text{1},\text{2},\text{3},\text{4}$ ， $x_{\text{4}}=ict$ ；积分路径L是在粒子束中从积分初始点x₀到x的任意可积路径，它不是粒子轨迹而是计算场的数学路径。现在考虑碰撞中的粒子1和2，如图1所示，它们的相对论物质波为

$\begin{array}{l}{\varphi }^{\left(1\right)}=\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x\left(p_{\mu }^{\left(1\right)}+q^{\left(1\right)}{A}_{\mu }^{\left(1\right)}\right)\text{d}{x}_{\mu }}\right)=\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}_{\mu }^{\left(1\right)}\text{d}{x}_{\mu }}\right)\\ {\varphi }^{\left(2\right)}=\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x\left(p_{\mu }^{\left(2\right)}+q^{\left(2\right)}{A}_{\mu }^{\left(2\right)}\right)\text{d}{x}_{\mu }}\right)=\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}_{\mu }^{\left(2\right)}\text{d}{x}_{\mu }}\right)\end{array}$ , (2)

Figure 1. Particle 1 collides off particle 2

图1. 粒子1与粒子2的碰撞

本文中用上标来标注粒子1或2。粒子1与粒子2相距r，两者彼此提供的库仑四维矢势为

$\begin{array}{l}{A}_{\mu }^{\left(1\right)}=\frac{1}{4\pi {\epsilon }_0}\frac{q^{\left(2\right)}{u}_{\mu }^{\left(2\right)}}{c^{2}r}\propto p_{\mu }^{\left(2\right)}\\ A_{\mu }^{\left(2\right)}=\frac{1}{4\pi {\epsilon }_0}\frac{q^{\left(1\right)}{u}_{\mu }^{\left(1\right)}}{c^{2}r}\propto p_{\mu }^{\left(1\right)}\end{array}$ . (3)

相对论物质波表达式中的符号 $R=p+qA$ ，实际是经典分析力学的粒子正则动量 [8]。根据方程(2)，R可以写成漂亮的矩阵形式

$\begin{array}{l}\left[\begin{array}{c}{R}_{\mu }^{\left(1\right)}\\ R_{\mu }^{\left(2\right)}\end{array}\right]=\left(1+\left[\begin{array}{cc}{S}^{\left(11\right)}& S^{\left(12\right)}\\ S^{\left(21\right)}& S^{\left(22\right)}\end{array}\right]\right)\left[\begin{array}{c}{p}_{\mu }^{\left(1\right)}\\ p_{\mu }^{\left(2\right)}\end{array}\right]\\ \text{or}R=\left(1+S\right)p\end{array}$ . (4)

对于纯库仑相互作用，矩阵S具有最简单的形式，即它有 $S^{\left(\text{11}\right)}=0$ ， $S^{\left(\text{22}\right)}=0$ ，与方程(3)一致；对于一般情况下的复杂相互作用，很容易证明，矩阵S是Hermite矩阵(Hermitian Matrix)，即： $S^{+}=S$ ，因为 $\left|{\varphi }^{\left(\text{1}\right)}\right|=\left|{\varphi }^{\left(\text{2}\right)}\right|=\text{1}$ ，证明见附录A。

根据群论，二阶的Hermite矩阵S是由Pauli矩阵线性组合而成，具有SU(2)对称性：

$\left[\begin{array}{c}{R}^{\left(1\right)}\\ R^{\left(2\right)}\end{array}\right]=\left(1+S\right)\left[\begin{array}{c}{p}^{\left(1\right)}\\ p^{\left(2\right)}\end{array}\right]=\left(1+c_1{\sigma }_1+c_2{\sigma }_2+c_3{\sigma }_3\right)\left[\begin{array}{c}{p}^{\left(1\right)}\\ p^{\left(2\right)}\end{array}\right]$ ,(5)

这里Pauli矩阵(SU(2) group)是

${\sigma }_1=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],{\sigma }_2=\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right],{\sigma }_3=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ , (6)

这里c₁，c₂，c₃是三个相互独立的实数(以下称之为SU(2)群系数)。对于一般情况下的复杂相互作用，下面我们详细讨论上述公式中每一项Pauli矩阵的物理意义。

1) 假设在碰撞过程中c₁工作， $c_{\text{2}}=c_{\text{3}}=0$ ，这种情况是

$\left[\begin{array}{c}{R}_{\mu }^{\left(1\right)}\\ R_{\mu }^{\left(2\right)}\end{array}\right]=\left(1+c_1\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\right)\left[\begin{array}{c}{p}_{\mu }^{\left(1\right)}\\ p_{\mu }^{\left(2\right)}\end{array}\right]$ .(7)

容易看出，使用方程(3)来确定系数c₁，它代表了两粒子之间的纯库仑相互作用：

$\left[\begin{array}{c}{R}_{\mu }^{\left(1\right)}\\ R_{\mu }^{\left(2\right)}\end{array}\right]=\left[\begin{array}{c}{p}_{\mu }^{\left(1\right)}\\ p_{\mu }^{\left(2\right)}\end{array}\right]+\left[\begin{array}{c}{q}^{\left(1\right)}{A}_{\mu }^{\left(1\right)}\\ q^{\left(2\right)}{A}_{\mu }^{\left(2\right)}\end{array}\right]$ . (8)

在这种情况下，R就是我们比较熟悉的粒子在电磁场中的正则动量，R控制着物质波的相位。

2) 假设在碰撞过程中c₁和c₃工作， $c_{\text{2}}=0$ ，这种情况是

$\begin{array}{c}\left[\begin{array}{c}{R}_{\mu }^{\left(1\right)}\\ R_{\mu }^{\left(2\right)}\end{array}\right]=\left(1+c_1\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]+c_3\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\right)\left[\begin{array}{c}{p}_{\mu }^{\left(1\right)}\\ p_{\mu }^{\left(2\right)}\end{array}\right]\\ =\left(1+c_3\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\right)\left[\begin{array}{c}{p}_{\mu }^{\left(1\right)}\\ p_{\mu }^{\left(2\right)}\end{array}\right]+\left[\begin{array}{c}{q}^{\left(1\right)}{A}_{\mu }^{\left(1\right)}\\ q^{\left(2\right)}{A}_{\mu }^{\left(2\right)}\end{array}\right]\end{array}$ .(9)

让我们观察一下两粒子体系的总正则动量，它们是

$\begin{array}{l}{R}_4=R_4^{\left(1\right)}+R_4^{\left(2\right)}\\ R=R^{\left(1\right)}+R^{\left(2\right)}\end{array}$ .(10)

把方程(9)代入上式(10)，我们得到

$\begin{array}{l}{R}_4=p_4^{\left(1\right)}+c_3{p}_4^{\left(1\right)}+q^{\left(1\right)}{A}_4^{\left(1\right)}+p_4^{\left(2\right)}-c_3{p}_4^{\left(2\right)}+q^{\left(2\right)}{A}_4^{\left(2\right)}\\ R=p^{\left(1\right)}+c_3{p}^{\left(1\right)}+q^{\left(1\right)}{A}^{\left(1\right)}+p^{\left(2\right)}-c_3{p}^{\left(2\right)}+q^{\left(2\right)}{A}^{\left(2\right)}\end{array}$ . (11)

所以

$c_3=\frac{p_4^{\left(1\right)}+q^{\left(1\right)}{A}_4^{\left(1\right)}+p_4^{\left(2\right)}+q^{\left(2\right)}{A}_4^{\left(2\right)}-R_4}{p_4^{\left(2\right)}-p_4^{\left(1\right)}}$ , (12)

$c_3=\frac{\left|p^{\left(1\right)}+q^{\left(1\right)}{A}^{\left(1\right)}+p^{\left(2\right)}+q^{\left(2\right)}{A}^{\left(2\right)}-R\right|}{\left|p^{\left(2\right)}-p^{\left(1\right)}\right|}$ . (13)

回忆起c₃是SU(2)对称群的一个实数系数，在方程(12)中c₃通过能量变化来计算；而在方程(13)中c₃通过动量变化来计算，方程(12)和方程(13)都具有数学奇异性：如果分子不为零，方程(12)不允许两粒子具有相同的相对论能量，否则它的计算式分母为零从而使得两粒子之间的相互作用急剧增强(假设两粒子之间不是共振关系)；方程(13)同样不允许两粒子具有相同的相对论动量。这正是Pauli不相容原理。根据上述公式，Pauli不相容原理可以表述为：两粒子(费米子)不能具有相同的相对论能量E_r和不能具有相同的相对论动量，即

$p_4=\frac{mic}{\sqrt{1-v^2/c^2}}=\frac{i{E}_r}{c};p_4^{\left(2\right)}\ne p_4^{\left(1\right)};p^{\left(2\right)}\ne p^{\left(1\right)}$ . (14)

如果两粒子体系处于总的静态(in total stationary state)，它们的总物质波是

${\varphi }^{\left(1\right)}{\varphi }^{\left(2\right)}=\varphi \left(x^{\left(1\right)},x^{\left(2\right)}\right)\exp \left(-\frac{iE}{\hslash }t\right)$ ,(15)

而

$\begin{array}{c}{\varphi }^{\left(1\right)}{\varphi }^{\left(2\right)}=\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}_{\mu }^{\left(1\right)}\text{d}{x}_{\mu }+\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}_{\mu }^{\left(2\right)}\text{d}{x}_{\mu }}}\right)\\ =\exp \left(\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}^{\left(1\right)}\cdot \text{d}{x}^{\left(1\right)}}+\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x{R}^{\left(2\right)}\cdot \text{d}{x}^{\left(2\right)}}+\frac{i}{\hslash }{\displaystyle {\int }_{x_0\left(L\right)}^x\left(R_4^{\left(1\right)}+R_4^{\left(2\right)}\right)\text{d}{x}_4}\right)\end{array}$ , (16)

比较方程(15)和方程(16)，我们发现，总的能量守恒方程就是

$R_4=R_4^{\left(1\right)}+R_4^{\left(2\right)}=\frac{iE}{c}=const.$ .(17)

这就是R₄的物理意义，据此我们看出：R代表系统总的正则动量。注意到在(11)式子中R不仅包含电磁矢势A，还包含了新的成分。一般来讲，群参数c₃不为零，在方程(12)中的分子包含了两粒子之间的电磁相互作用，代入两粒子之间的库仑势，我们得到

$q^{\left(1\right)}{A}_4^{\left(1\right)}+q^{\left(2\right)}{A}_4^{\left(2\right)}=\frac{1}{4\pi {\epsilon }_0}\frac{q^{\left(1\right)}{q}^{\left(2\right)}{u}_4^{\left(2\right)}}{c^{2}r}+\frac{1}{4\pi {\epsilon }_0}\frac{q^{\left(1\right)}{q}^{\left(2\right)}{u}_4^{\left(1\right)}}{c^{2}r}\propto \frac{1}{r}$ ,(18)

它反比于两粒子之间的距离r。在电子费米气体中，群参数c₃应该与温度有关，所以方程(12)和方程(13)合并在一起而写成下述函数形式

$c_3=\frac{H\left(T,1/r\right)}{p_4^{\left(2\right)}-p_4^{\left(1\right)}}+\frac{M\left(T,1/r\right)}{\left|p^{\left(2\right)}-p^{\left(1\right)}\right|}$ , (19)

对于电子费米气体，让实验来决定上述分子中的因子 $H\left(T,1/r\right)$ 和 $M\left(T,1/r\right)$ 。只看粒子1和它的群参数，它的物质波的R最后写成

$R_{\mu }^{\left(1\right)}=p_{\mu }^{\left(1\right)}+\left(\frac{H\left(T,1/r\right)}{p_4^{\left(2\right)}-p_4^{\left(1\right)}}+\frac{M\left(T,1/r\right)}{\left|p^{\left(2\right)}-p^{\left(1\right)}\right|}\right)p_{\mu }^{\left(\text{1}\right)}+q^{\left(1\right)}{A}_{\mu }^{\left(1\right)}$ . (20)

粒子1相当于处在一个新的等效电磁场中：

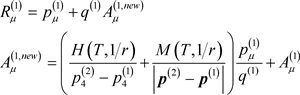. (21)

新的等效电磁场的第一项代表了Pauli不相容原理，第二项代表了纯库仑相互作用。方程(21)式给出了强关联电子体系的相互作用公式。

3) 假设在碰撞过程中c₁和c₂工作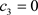，，这种情况是

. (22)

既然这种情况的相互作用矩阵S包含纯虚数，我们不得不考虑动量也有相应的如下的实部和虚部

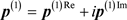. (23)

在四维空间中，它的形式是

. (24)

在这种情况下，只看粒子1，使用微扰理论(c₂是小量)，从(22)式我们有

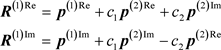. (25)

四维动量为p⁽¹⁾的粒子1可以看成一对“配对粒子”：动量分别为p^(1)Re和p^(1)Im，如何处理配对粒子显然是非常棘手的问题，长话短说，在本作者的早期论文 [9] 中使用微扰理论(c₂是小量)，p^(1)Re和p^(1)Im代表了自旋朝上和自旋朝下的配对关系，这里不再赘述。

3. 相对论物质波对超导电性的解释

本节我们将使用新的等效电磁场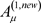来研究超导体中的电子费米气体。考虑两个相邻的电子，它们的物质波具有SU(2)对称性关系，如下

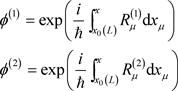, (26)

. (27)

这两个物质波的相位都是由3个部分组成：1) 两个粒子之间的库仑相互作用，由SU(2)对称群的第一个实数参数c₁表示；2) 两个粒子之间的自旋相互作用，由SU(2)对称群的第二个实数参数c₂表示；3)两个粒子之间的Pauli不相容的相互作用，由SU(2)对称群的第三个实数参数c₃表示。

在这篇论文中，我们只讨论库仑相互作用和Pauli不相容的相互作用，忽略自旋相互作用 [9]，即我们总是假定。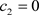

在超导体的电子费米气体中，在费米能表面上考虑两个相邻的电子1和电子2，它们分别具有能量E₁和E₂。如果电子1由于热运动而撞击晶格并且希望跳跃到较高的一个能级E₃上，即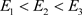，那么电子1会遇到麻烦：它的能量从E₁增加到E₃的过程中总会有一个时刻等于E₂，上节所述的Pauli不相容的相互作用的公式告诉我们，Pauli不相容的相互作用公式会变成无穷大，因为当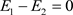时它的公式分母为零；实际上，新的等效电磁场会阻止这种跳跃，即当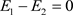时它的公式分母为零时Pauli不相容的相互作用变成无穷大(排斥力)从而禁止粒子1跳跃过程中它的能量接近相邻电子2的能量E₂。如图2(a)所示意。

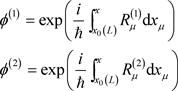. (28)

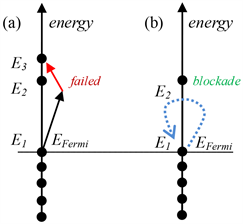
Figure 2. Electronenergy level distribution near the Fermi energy in the electron gas

图2. 电子气费米能附近的电子能级分布

这叫做“奇异性阻塞效应”(singularity blockade effect)。这个效应导致电子2会阻止任何一个与它相邻的电子跳跃到高于E₂的能级上去，如图2(b)所示意。这个奇异性阻塞效应也意味着费米能表面上的相邻的电子之间存在能隙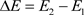。电子1可以做热运动，E₁可以在一定范围内涨落，但是电子1的能量不能超过电子2的能量E₂。同时，费米能表面内部的电子没有热运动，因为内部电子之间的奇异性阻塞效应比较强(跟费米能表面相比)，只允许非常弱的可以忽略的热运动，这叫做“囚牢效应”(jail effect)。图2(b)告诉我们，能隙至少要具有一个电子热运动的平均动能3kT/2的数量级，考虑到热运动电子的动能分布为Maxwell分布，所以在超导体中由于奇异性阻塞效应，能隙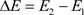的估计值应该在如下的范围内

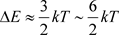. (29)

这里k是Boltzmann常数。能隙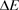是发生在费米能表面上的，只有少数电子具有较高的能级E₂，而这些少数较高能量的能级E₂的电子作为局域领导者控制着附近的电子，如图3所示意。

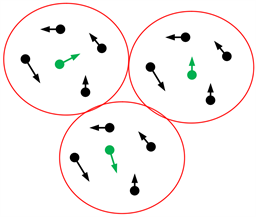
Figure 3. Only a few E₂ electrons become local leaders bullying over other neighboring electrons

图3. 少数较高能量的能级E₂的电子作为局域领导者控制着附近的电子

如何降低Pauli不相容的排斥相互作用呢？根据方程(28)的第一项，如果两个电子相距很远，它(既c₃)的分子必须下降并趋于零，这样分子才能消除分母为零的奇异性。所以，Pauli不相容的相互作用只对相邻的电子起作用。降低Pauli不相容的排斥相互作用的另外一个方法是让温度下降并接近零，这样两个电子之间的相互作用很弱，(28)式分子也会趋于零，结果在费米能表面上的能隙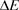也跟着变窄。

假设电子1跟晶格发生碰撞而获得一个声子的能量：

. (30)

这里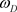是晶格Debye频率，根据Debye频率的定义，这个声子已经是晶格中能量最大的声子了。我们会有疑问：电子2作为局域领导者是否会允许电子1吸收这个声子？假如能隙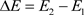小于这个声子的能量E_D，那么电子2就会利用奇异性阻塞效应来阻止电子1吸收这个声子，迫使电子1放弃吸收这个声子，这种情况发生的条件是

. (31)

结果，电子1在与晶格发生碰撞的过程中，在与这个声子的交互的过程中，既没有吸收能量也没有损失能量，这等效于电子与晶格之间发生了弹性碰撞，它意味着电子1在与晶格发生碰撞的过程中保持零电阻。所以，在温度下降到临界温度T_c时，能隙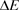等于或小于声子的最大能量E_D的时候，许多电子1在与晶格发生碰撞的过程中既没有吸收能量也没有损失能量，在奇异性阻塞效应控制下，超导现象发生了。所以，临界温度T_c为

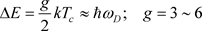. (32)

根据奇异性排斥效应，我们查阅了21种超导材料的能隙，如表1所列 [1]，与我们的估计值完全相符。

Table 1. Comparison of energy gaps for 21 typical superconductors

表1. 21种超导材料的能隙比较

本文所说的强关联量子体系中的相互作用公式(28)有一个显著的特点：不是改善超导体的能隙计算精度，而是给我们提供了一个新的超导机制：成功地解释了为什么有些电子(不是全部电子)能够在与晶格发生碰撞的过程中既没有吸收能量也没有损失能量，这等效于电子与晶格之间的弹性碰撞机制，虽然我们没有讨论自旋相互作用。不难想象，相同的奇异性阻塞效应可以用来解释液氦低温下的超流现象：碰撞过程中既没有吸收能量也没有损失能量，虽然液氦有些是费米系统(³Hellium liquid, superconductor)，有些是玻色系统(⁴Hellium liquid, excitons) [2]。

实际上，奇异性阻塞效应属于三体效应(电子1，电子2，声子)，与传统的量子波动方程求解思路相比，相对论的物质波公式通过相位变化的计算更加适合求解这类问题。其实，相对论物质波还有许多新的特性有待研究 [7] [9] [10] [11]，下面介绍相对论物质波的理论基础。

4. 相对论物质波的概念基础：平等性原理

在物理学中，一个粒子的四维速度u满足

. (33)

无论哪一种粒子(电子，分子，中子，夸克)，它们的四维速度u都具有相同的数量大小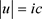：。在相对论时空中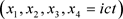，四维速度u具有平等性:对所有的粒子，四维速度u具有相同的数量大小，这叫做速度平等性原理。

假如电子具有最大极限加速度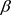，即任何电子的加速度都不能超过这个最大极限加速度，那么电子的相对论加速度应当满足

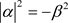. (34)

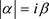对所有的电子，相对论加速度具有相同的数量大小，这叫做加速度平等性原理。很明显，这里的相对论加速度概念对传统的动力学公式有很大的冲击。实际上，我们希望看到：这里的加速度平等性原理能够导致粒子的Heisenberg不确定原理并且可以解释粒子的量子力学行为。为了达到这样的目的，我们下面讨论一下平等性原理与物质波之间的关系。

在一个实验室坐标系中，考虑一个质量为m的速度为v粒子，根据勾股定理(Pythagoras theorem)，在时间间隔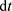内，粒子移动的距离为

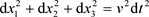. (35)

两边同时减去，我们得到

. (36)

它可以重新写成

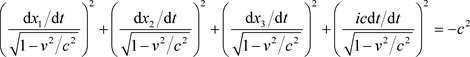. (37)

我们定义第四坐标轴和固有时间间隔(proper time interval)如下

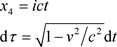. (38)

那么，坐标系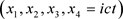构成了一个相对论时空，粒子的四维速度定义为

. (39)

我们有

. (40)

它意味着任何粒子的四维速度的数量大小取相同的值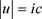： (常虚数)，这叫做速度的平等性原理。

根据勾股定理(Pythagoras theorem)，粒子的相对论加速度a有

. (41)

假如电子具有最大极限加速度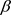，即没有电子的加速度能超过这个最大极限加速度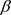，那么上式两边同时减去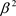，我们有

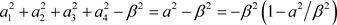. (42)

它可以写成

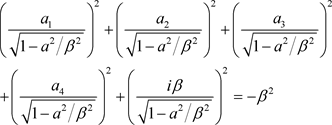. (43)

现在，上式左边包含五项，电子的相对论加速度可以看成五维加速度，定义为

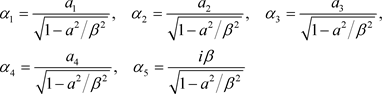. (44)

这里是新定义的第五维加速度，其五维相对论空间是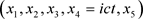，这样我们有

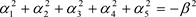. (45)

它意味着任何粒子的相对论加速度的数量大小取相同的值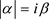： (常虚数)，这叫做加速度的平等性原理。

每一个电子的相对论加速度的数量大小取固定值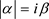：，每一个电子的相对论速度u的数量大小也取固定值：，这是一种怎样的运动图像？在现实世界中，当一个小轿车做匀速圆周运动的时候，它具有常切向速度v和常向心加速度a，如图4所示。

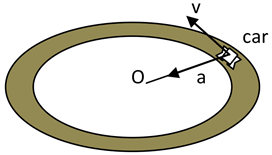
Figure 4. A car moves around a circular path at constant speed v with constant centripetal acceleration a

图4. 小轿车做匀速圆周运动的时候，它具有常切向速度v和常向心加速度a

Figure 5. The electron moves along the x₁ axis with the constant speed in the u direction and constant centripetal force in the x₅ axis at the radius iR (imaginary number), the coordinate system consists of a cylinder coordinate system

图5. 一个沿着x₁轴以速度v做匀速运动的电子，它在图中沿着u方向以常速度运动和沿着x₅轴方向以常加速度做半径iR (虚数)的圆周运动，它的坐标系构成柱坐标系

类似于匀速圆周运动的小轿车，如图5所示，考虑一个沿着x₁轴以速度v做匀速运动的电子，它在图中沿着u方向以常速度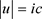运动和沿着x₅轴方向以常加速度做半径iR (虚数)的圆周运动，它的坐标系构成柱坐标系，在其中，电子沿着x₁轴以速度v做螺旋运动。根据我们熟知的向心加速度公式，在x₄-x₅平面的向心加速度是

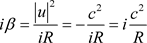. (46)

所以，在这个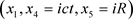柱坐标系中电子的轨迹形成一个螺旋包(spiral-package)，电子运动速度v越快，螺旋步距越长。而在狭义相对论的时空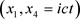中这个螺旋包是不可见的。

图5中的螺旋包像一个钢丝弹簧，可以用一个波函数来描述；电子向前运动137个螺旋步距(spiral step)，对应波函数相位增加2p，137个螺旋步距对应螺旋周长是137 ×2p(iR)。为什么是137个螺旋步距对应相位2p呢？因为它与精细结构常数f = 1/137相关联。既然电子在螺旋线上的每个微小位移是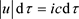(在四维速度u的方向上)，波函数相位增加量的计算公式为

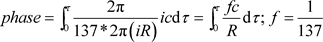. (47)

代入半径R，波函数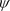表示为

. (48)

在相对论理论中，我们知道沿着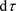的积分需要换算成现实世界的线积分，也就是

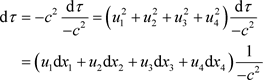. (49)

所以波函数表达式为

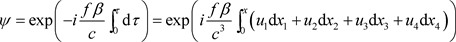. (50)

容易发现，最大极限加速度是一个傀儡，它是普兰克常数(Planck constant)的代理，那么波函数表示为

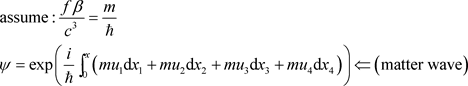. (51)

注意到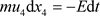，上面这个方程(51)强烈建议上述波函数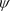就是现实世界的德布罗意物质波(de Broglie matter wave)。

讨论：1) 平等性原理是一个很好的物理基础平台，它可以让我们合理地引入基本常数。因为它让每个粒子都平等地享有相同的物理学基本常数。正如我们利用速度平等性原理和加速度平等性原理，让每个电子都在运动的时候享有相同的速度数量大小和相同的普兰克常数，就像电子生命中的不变基因。2)实际上，平等性原理为传统物理学注入了新鲜血液，特别是对天体物理，超导电性等等。平等性原理特别适合用来建立物理学的基本概念。3) 在图5中，电子在这个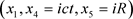柱坐标系中螺旋步距是

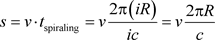. (52)

螺旋步距对应的螺旋周期是一个常数。在本文中，电子在这个柱坐标系中的螺旋轨迹叫做螺旋包(spiral-package)，螺旋包的长度被认为是物质波的相干长度(coherent length)。4) 在图5中，电子的螺旋包有2种：顺时针螺旋包和逆时针螺旋包，本作者认为它们可以代表自旋朝上和自旋朝下。很容易计算出电子在做螺旋包运动时候的相心加速度(ultimate acceleration)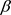，半径R以及角动量J，如下

. (53)

在图6中，角动量J的方向会与电子前进的x₁方向稍微不同，因为角动量J在绕着x₁方向做进动，这是由于螺旋包造成的。很容易想到这个角动量J会被现实世界的外部磁场B捕获到。如何把这个角动量J投影到现实世界中去，如何与自旋朝上和自旋朝下相关，如何与高能粒子的手征(chirality)相关，这些问题超出了本文预设的范围，参见文献 [9]。

重要提示：实际上，人们在狭义相对论时空中是看不到上述螺旋包；人们只有在柱坐标系时空中才能看到上述螺旋包。

如图7所示，螺旋包的长度被认为是物质波的相干长度(coherent length)，相应地，相干宽度(coherent width)是指物质波在横向的影响范围(不是指在x₅轴上的螺旋包半径R，因为在现实世界时空中看不到x₅轴)。螺旋包限制在相干长度(coherent length)和相干宽度(coherent width)之间。

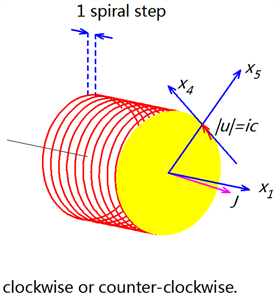
Figure 6. The direction of the angular momentum J would be different from the advance x₁ direction

图6. 角动量J的方向会与电子前进的x₁方向稍微不同

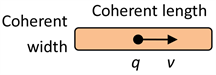
Figure 7. The length of spiral-package is recognized as the coherent length of its matter wave

图7. 螺旋包的长度被认为是物质波的相干长度

Figure 8. The component spectrum is a sharp about k₀

图8. 波谱成分在k₀处有一个峰值

很明显，螺旋包就是一个波包。考虑一个电子沿着x轴运动，它的物质波具有相干长度L，物质波的波包是

. (54)

它的波谱成分可以写成为

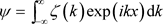. (55)

既然波包中不同成分的传播速度不同，各种波谱成分可以由傅里叶分析得到

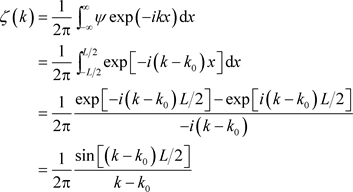. (56)

现在，显然sinz/z在有最大值，在和处下降到零。对于较大的L，波谱成分在k₀处有一个峰值，如图8所示，它是一个动量确定而位置不确定的电子波包情形。波谱成分的傅里叶分析告诉我们，不确定关系是

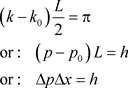. (57)

这就是Heisenberg不确定原理。我们可以放心地说，电子不是一个几何点，它生活在它的非现实世界的螺旋包中。

位置，速度，加速度是粒子物理学中的三个基本概念，对应地，我们有位置平等性原理，速度平等性原理，加速度平等性原理。位置平等性原理要求我们承认存在一个最大极限距离D，它自动被认为是宇宙直径：在D范围内，无物体可以逃脱。位置平等性原理允许我们引入哈勃常数(Hubble constant)和解释哈勃定律(Hubble law)。

考虑一个遥远恒星，它到太阳的距离为d，我们以太阳为原点建立一个参考坐标系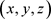，如图9所示，勾股定理(Pythagoras theorem)告诉我们

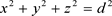. (58)

Figure 9. Afar star in the sun reference frame

图9. 太阳系中一个遥远的恒星

因为距离d是一个很大的距离，我们自然会担心非欧几何效应(non-Euclidian effect)对位置测量产生的影响，修改位置的测量公式为

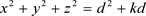. (59)

这里kd项代表非欧几何效应。假设在宇宙中存在这个最大极限距离D，那么上式两边同时减去D²，

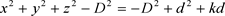. (60)

它可以被写成

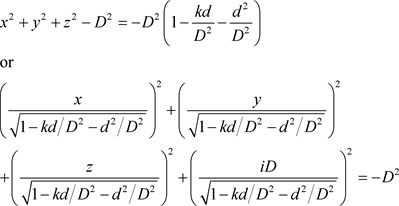. (61)

那么一个新坐标系必须建立起来，新坐标系定义为

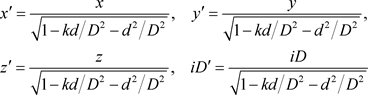. (62)

在这个新坐标系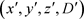中，所有的星球相对于这个坐标原点的位置都具有相同数量大小：

. (63)

位置的数量大小是相同的！这个叫做位置平等性原理。

现在我们用哈勃定理来测试一下位置平等性原理。考虑一个遥远的位置的原子，它发射出一束波长l的电磁波。我们必须保证位置平等性原理，所以我们实际上生活在新坐标系中，我们看到

. (64)

根据(64)式的第一个式子，在我们的新坐标系原点接受到的电磁波的波长是

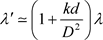. (65)

这就是哈勃定理(Hubble law)，而D²/k等于哈勃常数(Hubble constant)。位置平等性原理的优点是，不需要让遥远星系按照多普勒效应预言的那样退行(或宇宙膨胀)。宇宙红移，或者宇宙蓝移，多普勒效应，宇宙膨胀，这些问题困扰了人们很长时间，有了位置平等性原理，我们对宇宙的认识将更近一步。

5. 结论

相对论物质波为超导体中的量子强关联体系的研究提供了一个基本概念。本文通过研究电子碰撞过程中相对论物质波的相位变化，推导出了强关联电子体系的相互作用公式，并对其在超导体中的有效性进行了检验。我们对超导能隙的计算与典型的21种超导体的实验结果吻合得很好。此外，这个相互作用公式清楚地表明，在极低温度下，某些电子与晶格的碰撞将变得既无能量增益又无能量损失，从而为超导机制的研究提供了新的思路。另外，我们提出，相对论物质波是建立在平等性原理基础上的基本概念，从而使得我们的超导理论有更加扎实的理论基础。

附录A

定理1：相互作用矩阵S是Hermite矩阵，即。

证明：在多粒子体系中，第j个粒子的物质波是

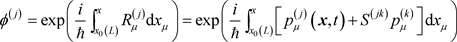, (A1)

这里重复的指标表示求和运算(Einstein求和约定)，除非另有说明。我们定义自由粒子的物质波

, (A2)

考虑S是相互作用的小量，那么我们有

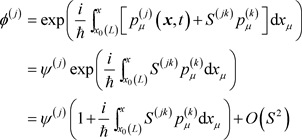. (A3)

典型地，我们要求物质波满足归一化条件：

. (A4)

这里

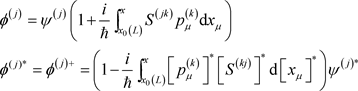, (A5)

上式中使用的置换操作是为了与后面遇到的矩阵乘法运算规则一致。我们有

. (A6)

我们知道

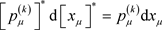. (A7)

这样

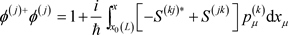. (A8)

积分路径L是在粒子束中从积分初始点x₀到x的任意可积路径，它不是粒子轨迹而是计算场的数学路径；所以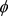，的归一化导致了我们的结论

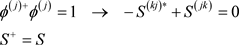. (A9)

证明完毕。