摘要: 地球化学元素分布规律的研究是揭示元素成矿及空间变化规律的重要途径之一。以新疆雅山荒漠地区为例,选取两类矿质,结合多重分形,利用多重分形矩估计法对荒漠两地区的土壤中元素进行全量分析,从奇异性和非对称指数方面,进一步探讨元素的非线性迁移,为以后荒漠区找矿提供一种新的方法和方向。从结果我们可以看出,成矿元素Mn在I区和II区的土壤中分布均具有连续的多重分形特征,随后通过对比两区域的奇异指数和非对称指数发现,奇异指数和非对称指数的值I区均大于II区,由此可以推断出I区迁移特征要高于II区,所以说元素的多重分形特征对于荒漠区找矿具有一定的指示意义。
Abstract:
The study of the distribution law of geochemical elements is one of the important ways to reveal the law of element mineralization and spatial change. Taking the desert region of Yashan, Xinjiang as an example, two types of minerals are selected, combined with multiple fractals, and multiple fractal moment estimation methods are used to conduct a full analysis of the elements in the soil in the two desert regions. From the aspects of singularity and asymmetric index, the non-elements of the elements are further explored. Linear migration provides a new method and direction for prospecting in the desert areas in the future. From the results, we can see that the distribution of the ore-forming element Mn in the soils of regions I and II has continuous multifractal characteris-tics. Then, by comparing the singular and asymmetric indices of the two regions, we find that the singular and asymmetric indices for the values of area I are larger than area II. It can be inferred that the migration characteristics of area I are higher than area II. Therefore, the multifractal characteristics of the elements have certain significance for ore prospecting in desert areas.
1. 引言
现在已有许多应用非线性理论方法解决复杂地质问题的成功试验。於崇文 [1] 提出了关于地球系统的复杂性和成矿系统,例如“矿床在混沌边缘生长”。谢淑云等 [2] 通过蒙古白音诺尔铅锌矿床元素的总量测试研究,对系统模拟和研究地球化学组分在矿区及周边残积土剖面中的迁移演化规律及其影响因素亦具有指示意义。申维 [3] 发表了成矿预测的分形理论。分形和多重分形普遍存在于地球化学的研究中,成秋明 [4]、肖凡等 [5] 从奇异性的角度,评述了非线性理论在成矿动力学和矿产勘查中的应用 [6] [7] [8],以及非常规矿床与非常规矿产资源评价的研究现状。李晓晖等 [9]、刘舒飞 [10] 通过对元素进行奇异性指数的分析和计算,提取矿化有关信息。周杰等 [11] 利用多重分形理论对深层土壤Au元素进行弱缓化探异常信息的识别。
文章从全量方面进行Mn元素非线性迁移研究,拟通过对元素多重分形奇异性和非对称性两方面,分析元素迁移特征,为元素找矿提供新的方向。
2. 多重分形谱分析
分形最早由Hausdroff在1919年提出、后来Mandelbrot [12] [13] 将其推广。多重分形的分形维数不是单一不变的,多维分形的谱函数并非总是连续的 [14] [15] [16],分形特性多用多重分形谱
来表示,
表示奇异指数。有几种算法可用于计算
和
的值,较为常用的是矩估计法 [14] [17]。首先构造配分函数,设在任意大小为r的格子i中其密度为
,对
用q次方进行加权求和可以得到配分函数,质量指数
由Cheng [18] 引入,得到
的表达式:
(1)
(2)
(3)
由(2)、(3)式可看出,奇异指数
和多重分形谱函数
是多重分形谱的两个特征参数,将矩统计量与奇异指数
以及分形维数谱函数
相联系在一起 [19]。
元素的多重分形谱均表现为钩状且呈连续分布,
曲线均为不对称的上凸曲线,表明雅山荒漠地区土壤中重金属元素均经历过不同程度的叠加改造,且元素具备多重分形特征,不能用简单的单一分形模型来描述。为进一步找寻谱函数的形态特征的实际意义,引入非对称指数R,谢淑云等 [20] 曾运用该指数来判断元素分布的成矿潜力。
非对称指数R数学表达式为:
(4)
其中
。当
时,分形谱函数
曲线左右完全对称。R表示高含量部分的奇异性,值越大表示高含量部分在区域上平均密度变化差异大。
3. 数据来源
选取雅山Cu-Mo异常区内的钻孔ZK01-ZK05进行研究。覆盖层研究区土壤矿物成分主要有石英、长石等成分,ZK01、ZK02、ZK03底部为二长花岗岩,ZK04、ZK05底部为凝灰岩。ZK01、ZK02、ZK03归为I类,ZK04、ZK05归为II类,对这两类主要成矿元素进行参数分析。
4. Mn元素全量分析
文章采用矩估计法对雅山荒漠地区元素进行多重分形分析,对元素的奇异性特征进行讨论,其中元素的奇异指数
通过中心插值计算得到。文章从全量方面进行多重分形谱的分析(图1)。
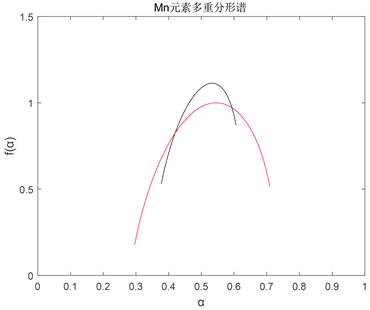
Figure 1. Total multifractal spectrum of Mn (red I, black II)
图1. Mn元素全量多重分形谱(红I,黑II)
Mn元素多重分形谱
均表现为钩状且呈连续分布,表明连续多重分形是金属地球化学场元素的一种普遍规律;同时,曲线
均为不对称的上凸曲线,表明元素均经历过不同程度的叠加改造,且元素具备多重分形特征 [21]。
Mn元素多重分形数据结果如表1所示,
代表谱开口宽度,
反映的是左右谱高差,R为非对称指数。从数学方面来分析,
显示元素高值区域和低值区域分布的比例,
越小,高值区域所占比例越大,分形谱函数
曲线的左半段主要反映了
的特征,能刻划分形的基本特征,而右半段为
部分主要反映了测量过程的各种误差或者干扰以及分形结构中的细小结构变化,也就是说低含量的特征能得到加强。开口宽度
反映了元素分布在整个测度上分布的均匀性和奇异性,
越大,说明元素在空间上的分布越不均匀。非对称指数R > 0且R值越大,不对称性越明显。从元素迁移方面来说,
越小,高值区域所占比例越大,在土壤中的活动性就越强,当地质系统受到微小扰动的时候,元素发生迁移的可能性就越大。
反映了元素分布在整个测度上分布的均匀性和奇异性,
越大,奇异性越大,属于越有利迁移的类型。非对称指数R > 0且R值越大,迁移特征越明显,R值的大小与主要成矿元素迁移潜力有一定的对应关系 [21]。

Table 1. Mn element multifractal result data
表1. Mn元素多重分形结果数据
由表1可以看出,覆盖层的多重分形特征I、II两区域Mn元素的
、
、R值均大于0,覆盖层的奇异性特征较强,元素含量的不均一性强,利于发生迁移。Mn元素的
、
、R值在I区较II区的值高,说明元素在I区土壤活动性较强,分布的不均匀性也较大,迁移特征明显,说明Mn元素在I区的迁移特征较为明显。
5. 结论
从全量方面对Mn元素在这两个地区的多重分形特征进行分析,通过实验发现元素具有多重分形特征且通过实验结果对比元素的谱宽、高度差、非对称指数,结果显示I区都是高于II区的,Mn元素在I区迁移特征要高于II区,说明I区更利于元素迁移,为雅山地区的找矿提供了新的思路和方法。
基金项目
本文依托于国家自然科学基金面上项目(NO. 41872250)“荒漠覆盖层成矿元素垂向迁移的非线性响应机理研究”和中国地质调查局项目“覆盖区弱异常形成机理与地球化学勘查”(12120113088900)选择新疆雅山荒漠覆盖区的Cu-Mo异常区作为研究对象,通过野外地质勘察、收集并分析前人的研究成果,为荒漠地区找矿提供理论支撑。