1. 引言
随着国民经济水平的增长,人类对于电力资源的需求也在不断增大,因此社会对于电力电缆的安全使用也有了更高的要求。电缆由于长期运行在高电压、强电流的环境下,容易引起温度上升、温度异常等情况 [1],因此,准确检测电力电缆的温度对电缆的使用寿命及安全保障具有重大意义。
目前对电缆温度进行监测的方法主要有两类:一类是电信号监测技术 [2];利用合适的传感器,将电缆温度转换为电信号,最终得出温度测量结果。主要方式有热电偶测温、热电阻测温、集成传感器测温等。另一类是光信号监测技术;通过检测光纤传感器中的光强、波长等值的变化,利用光纤传感特性得到外界温度测量结果。实现该类方法的途径主要有布里渊传感器测温法、拉曼传感器测温法、光纤光栅测温法等。
本课题采用光信号监测技术中的光纤光栅测温法,通过外界参量对布拉格光栅中心波长调制获得温度信息。光纤光栅传感器成本低、质量轻、体积小、易埋入材料,同时具有抗腐蚀、抗电磁干扰等优点 [3],适合在较恶劣环境下工作。当使用光纤光栅传感器对电缆温度进行测量时,通常将其放置于表皮处,而对于电缆来说,其缆芯温度值相对表皮温度值更加可靠,为了避免电缆热点检测中出现漏检漏报的现象,需对二者建立对应关系。目前可通过热路计算法来实现。本文提出一种新的计算方法——仿真计算法。通过与热路计算法对比,验证其可行性。
2. 光纤Bragg光栅的测温原理
光纤光栅能够使纤芯折射率沿轴向发生周期性改变,是一种衍射光栅。当外界温度、压力等发生变化时,纤芯内光栅栅距和周期会发生改变,进而引起波长漂移。
光纤Bragg光栅(fiber bragg grating, FBG)对于光波长具有一定的选择性,当宽带光源发出的光信号传输到光纤光栅上时,符合FBG波长的光信号被反射,其他波长的光则被透射 [4]。光纤Bragg光栅的传感原理如图1所示。
光纤Bragg光栅的谐振方程为:
(1)
其中:λB为光栅Bragg波长,neff为光栅有效折射率,Λ为光栅条纹周期。
由式(1)可知:温度引起的光纤光栅λB的变化,主要是因为温度改变会引起光纤光栅有效折射率和栅距的变化。忽略应力变化影响,由式(1)可得光栅波长的变化为:
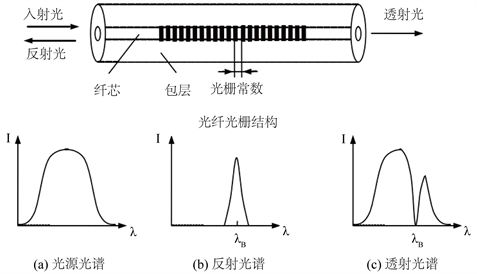
Figure 1. Sensing principle of fiber Bragg grating
图1. 光纤Bragg光栅的传感原理
(2)
其中:
为温度变化,
为光栅有效折射率变化,
为光栅周期变化。
设温度灵敏度系数为K,则:
(3)
由式(3)可得:
(4)
由式(4)可知,忽略外力作用,温度变化与光纤光栅波长变化成正比,故在对电缆温度进行计算时,可通过检测波长变化得到电缆温度值。
3. 电力电缆热路模型法
电力电缆在运行时,由于缆芯、绝缘层、铠装层等产生损耗会引起发热现象,从而导致电缆的温度升高。因此,需要对电缆的温度进行实时监测,以便掌握电缆的运行状态 [5],及时发现电缆的潜在隐患并进行有效处理。
IEC-60287标准 [6] 提供了具有代表性的电缆缆芯温度计算方法。缆芯发出的热量在扩散过程中,要经过除导体以外的所有结构;介质损耗产生的热量则要经过金属屏蔽层、铠装层、外护套等几部分;金属屏蔽损耗产生的热量要经过铠装层和外护套,而铠装损耗所产生的热量则只经过外护套。根据电力电缆的传热分析,得出其热路模型如图2所示 [7]。
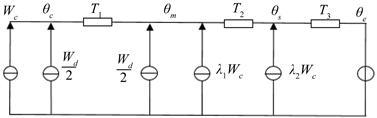
Figure 2. Power cable hot circuit model
图2. 电力电缆热路模型
其中,T1、T2、T3分别为等效绝缘层电阻、内护套电阻以及外护套电阻;θc、θm、θs、θe分别表示电缆的缆芯温度,绝缘层温度、内护套温度以及表皮温度;Wc表示导体功率损耗,Wd表示介质损耗,λ1表示金属屏蔽损耗系数,λ2表示铠装损耗系数。
从图2可以得出在稳态条件下,电力电缆的导体温度表达式为:
(5)
对于一般的电力电缆,只要给出准确的表皮温度值θe,就可通过式(5)进行理论计算,得出电力电缆的缆芯温度值θc。
4. 电力电缆的仿真分析法
计算电力电缆缆芯温度的另一种方法是仿真计算法。根据电缆参数以及敷设条件,准确得出电缆的温度场分布。
本课题采用的是ANSYS有限元分析法。通过分析电缆内部温度情况,建立表皮温度与缆芯温度之间的关系,得出温升方程。通过此方程,在对电缆进行实时监测时,就可直接测量电缆的表皮温度值来得到缆芯温度。
以三芯电缆YJLV22-10-3 * 100交联聚乙烯的技术参数为指标,进行仿真分析。首先在ANSYS Workbench电磁模块Max Well2D中创建电缆二维几何模型,设置材料、导热系数等参数。之后将产生的焦耳热损耗、涡流损耗以及介质损耗等充当热源,加入到稳态热分析模块Steady-State Thermal中,设置边界条件,对电缆温度场进行求解。电缆材料参数如表1所示 [8]。
电缆仿真模型由线芯、屏蔽层、填充层、内外护套等9部分组成。电缆模型结构参数如表2所示 [8]。
在不影响求解精度的情况下,为了方便求解,进行如下几个方面假设:
(1) 电缆横截面为标准圆形;
(2) 电缆材料参数分布均匀且属性不变;
(3) 边界温度均匀分布,设定为定值。
(4) 电缆层间紧密连接,忽略接触电阻。
基于上述假设,建立电力电缆的二维几何模型,如图3所示。
在对电力电缆进行求解时,既要保证求解精度,又要考虑到求解时间的大小,因此本课题采取的是自由网格划分,其中网格元素大小为0.0005 m,网格划分结果如图4所示。

Table 2. Cable structure parameters
表2. 电缆结构参数

Figure 4. Finite element of three-core cablemeshing
图4. 有限元网格划分
在ANSYS Workbench的电磁模块中,首先对电力电缆进行电磁分析,施加电流激励,求解损耗值,并将其作为热源加入到稳态热分析模块中。边界条件设置为对流,其中对流换热系数设置为5 W/m2*℃,边界环境温度设置为22℃。当施加的电流为120 A时,求解出的三芯电缆内部温度云图如图5所示。

Figure 5. Temperature cloud image of three-core cable
图5. 三芯电缆温度云图
由图5可以看出,电缆模型内最热部分为缆芯,温度最低部分为表皮。当施加不同的电流激励时,分别记录二者的温度值,结果如表3所示。

Table 3. Cable skin temperature and cable core temperature under different excitation
表3. 不同激励下电缆表皮温度与缆芯温度
根据表3中的仿真数据,通过MATLAB进行函数拟合,拟合直线如图6所示。

Figure 6. The line diagram of skin temperature and cable core temperature was fitted
图6. 表皮温度与缆芯温度拟合直线图
最终得出电缆表皮温度与缆芯温度之间关系:
(6)
其中,
为仿真计算得到的缆芯温度。
根据式(6),在对电缆进行实时监测时,就可直接通过测量电缆表皮温度值来计算得到缆芯温度值,无需在出厂时就将光栅放置于电缆缆芯处,节省经济成本。
5. 热路计算法与仿真计算法的比较
为了能更好的对热路计算法与仿真计算法结果进行比较,现将仿真三芯电缆YJLV22-10-3 * 100的具体参数代入到IEC-60287标准公式(5)中,计算可得:
(7)
输入一定电流激励,仿真得出表皮温度值
,将
分别代入式(6)与式(7)中,结果如表4所示。

Table 4. The results of the two formulas are compared
表4. 两种计算公式结果比较
通过表4可以看出,当输入电流激励为300 A,所测表皮温度为42.37℃时,热路计算缆芯温度为44.04℃,仿真计算缆芯温度为50.00℃,此时两种计算公式所得缆芯温度值差值最大,为+5.96℃。当输入电流激励为50 A,所测表皮温度为22.57℃时,热路计算缆芯温度为22.86℃,仿真计算缆芯温度为22.79℃,此时两种计算公式所得缆芯温度值差值最小,为−0.07℃。可见,两种推演方式最终计算结果是有差异性的。
由热路模型推导出的IEC-60287计算公式,对单芯电缆的计算结果较准确,而在使用热路计算法对三芯电缆温度进行计算时,是将其等效为单芯电缆,即将单芯电缆的材料参数乘以相应系数来进行计算的,这种等效计算方式本身就存在误差。其次,热路计算法在对热阻进行计算时,主要是凭借经验数据对电力电缆各层材料热阻进行等效,没有考虑到物体的形状结构对导热过程的影响。因此,热路计算法存在较大误差。
传热学中,形状因子是表示物体形状结构对导热过程影响的物理量,其大小取决于物体的形状和几何尺寸 [9]。为了能对电缆热阻更准确的进行计算,本文采用传热学中的形状因子法,即根据导热介质形状特征来对电缆热阻值进行修正。
在IEC标准中,各部分热阻计算公式为:
(8)
(9)
(10)
其中,P为屏蔽因素,G、 为几何因素,分别取0.78、0.997以及0.49;
、
、
分别为绝缘层、内护套以及外护套的热阻系数,分别取3.5 K·m/W、6.0 K·m/W、6.0 K·m/W;d为外护套的厚度,D为铠装层的外径。
由式(8)、(9)、(10)得出的热阻 、 、 分别为0.437、0.464、0.07。
根据传热学以及形状因子的定义可知导热介质的热阻与形状因子的关系为:
(11)
λ为导热系数,表1中已给出;S为形状因子。
绝缘层、外护套的形状因子计算公式为:
(12)
其中,对于绝缘层来说,R为电缆圆心到绝缘层半径,r为电缆圆心到导体屏蔽层半径;对于外护套来说,R为电缆圆心到外护套半径,r为电缆圆心到铠装层半径。
对于形状非圆环的填充层来说,形状因子的计算公式为:
(13)
其中,r2为电缆圆心到内护套半径,r1为电缆圆心到填充层半径,r0为填充层内部小圆的半径。
根据式(12)、(13)计算可得绝缘层、内护套、外护套的形状因子为18.28、20.07、71.36。
将其代入式(11)可得修正后的热阻系数为:
、
、
。
将修正后的热阻值代入式(5),可得到修正后热路计算的缆芯温度值θc2,其与修正前热路计算缆芯温度值以及仿真计算缆芯温度值的结果如表5所示。

Table 5. Thermal resistance coefficient modified after core temperature comparison
表5. 热阻系数修正后缆芯温度比较
通过上述分析,可知修正后的热阻值考虑到了形状结构对导热过程的影响,即修正后的热路计算法所得结果更准确。通过表5可看出,当表皮温度相同时,仿真计算法与修正前热路计算法相比,其结果更接近于修正后热路计算法。比如,当表皮温度为42.37℃时,修正前热路计算缆芯温度值与修正后热路计算缆芯温度值差值为4.01℃,仿真计算缆芯温度值与修正后热路计算缆芯温度值差值为1.95℃。由此可以看出,仿真计算法相对热路计算法而言,不用考虑形状因子,计算简便,适用性强。
6. 在线温度监测系统的设计
本测温系统由硬件和软件两部分组成。硬件部分包括电源、宽带光源、光纤光栅传感器、FBGA解调模块、环形器等,软件部分为基于LABVIEW开发的上位机模块。系统总体设计框图如图7所示。
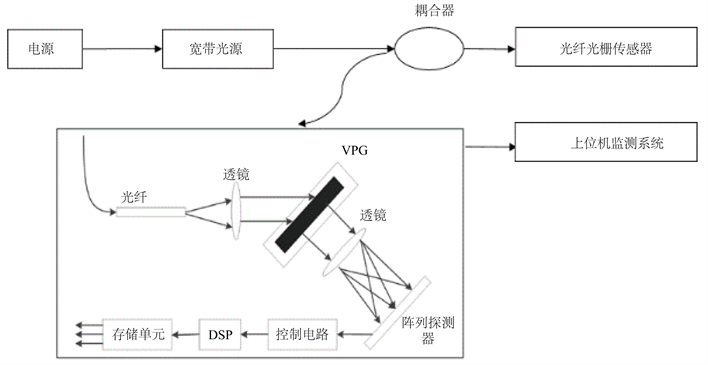
Figure 7. System overall design block diagram
图7. 系统总体设计框图
宽带光源发出的宽带光经环形器进入到光纤光栅传感器中,其中符合1550 nm波长的光信号被反射,其他波长的光被透射。被反射回来的光信号由环形器进入到FBGA解调模块中,当光源通过微透镜准直后,入射到体相位光栅上,经过多重体相位光栅的分光后入射到线阵PIN二极管阵列,完成光、电信号之间的转换 [10],通过检测PIN二极管阵列光强最大处,得出中心波长值。之后调用LABVIEW上位机系统,对上述信息进行处理,将电缆的温度值及光功率值实时显示到计算机上。
电缆温度监测界面是基于LABVIEW虚拟仪器软件建立的,同时能对温度、波长值进行实时采集以及显示 [11]。电缆温度监测界面如图8所示。

Figure 8. Cable temperature monitoring interface
图8. 电缆温度监测界面
在使用光纤Bragg光栅进行测温时,所搭建的实验平台如图9所示。

Figure 9. Fiber Bragg grating temperature measurement system
图9. 光纤Bragg光栅测温系统
7. 结束语
通过有限元仿真分析,得出电缆缆芯温度与表皮温度的温升方程,并与IEC-60287标准进行比较,仿真分析方法更简单。在对电缆进行实际测量中,可直接测量表皮温度而推演计算出缆芯温度,既降低了测温的难度,又提高了温度测量的准确度。
基金项目
辽宁省教育厅科学研究项目[LFGD2019006]。