山地环境重载六足机器人运动控制分析

Motion Control Analysis of Heavy-Duty Hexapod Robot in Mountainous Environment

摘要: 为了实现山地环境下重载六足机器人的稳定运动，提出了一种基于A-Star算法的图表搜索步态生成方法。选定六足机器人23种稳定支撑状态，建立支撑状态转换表，依据图表搜索法生成每条足腿从初始状态到目标状态可能的运动状态序列；再结合A-Star算法选定一条从根节点到目标节点的最优路径，以此作为足腿的最终运动状态序列；最后对足端轨迹进行多项式拟合，通过设定轨迹高度和宽度实现跨越不同障碍的能力。结果表明，本文提出算法运行在六足机器人模型上时，测得移动距离平均误差为7.2%，单腿足端运动轨迹的ADAMS仿真曲线过度平滑，能有效减少惯性抖振现象。该研究为山地环境下重载六足机器人的运动控制方法提供了参考。

Abstract: In order to realize the stable motion of heavy-duty hexapod robot in mountainous environment, a graph search method based on A-Star algorithm is proposed. Thirty-three kinds of stable support states of hexapod robot are selected, the transition table of support states is established, and the possible motion state sequence of each leg from initial state to target state is generated by graph search method. Then, an optimal path from root node to target node is selected by A-Star algorithm, which is used as the final motion state sequence of the leg. Finally, the foot trajectory is polynomially fitted, and the ability to cross different obstacles is achieved by setting the height and width of the trajectory. The results show that the average error of the proposed algorithm is 7.2% when it runs on the hexapod robot model, and the ADAMS simulation trajectory curve of the single leg foot is smooth, which can effectively reduce the inertial vibration phenomenon. This study provides a reference for the motion control method of heavy-duty hexapod robot in mountainous environment.

1. 引言

我国是多山国家，近1/3国土面积由山地环境组成，广泛分布于东北、东南、桂北、西南、粤桂滇南部以及沿海地区，同时我国与越南、老挝、缅甸等邻国的陆疆边界主要以山地地形相接壤，在这些区域，常规机器人无法通行和部署，是物资运输的重要障碍。为满足复杂环境物资运输需求，有必要研究山地环境重载足式机器人平台，使其能够承担山地环境下的物资补给、人员输送、边境巡逻、灾后营救、侦察警戒等任务。足式机器人按其结构形式多分为双足、四足、六足、八足 [1] [2] [3] [4]。本文主要以六足机器人为研究对象，相较于两足与四足机器人，它稳定性高，具有冗余的机械结构使之灵活性更强 [5] [6]，而八足机器人虽然稳定性更高，但由于腿的数量增加，自重增加，机构设计与控制的难度大幅度上升 [7]。因此，模仿昆虫及其他节肢动物门动物的肢体结构和运动控制策略 [8] 而创造出的六足机器人是一个较好选择，仿生六足机器人的研制已经在国内外成为热点 [9] [10] [11]。

目前，预研样机在研制过程中，遇到了系统陡坡行进能力差、载荷自重比小、功率配置高等难点问题，机器人实用化研制工作受到极大阻力，其根本原因在于缺乏对大尺度重载六足式山地机器人的移动行为、运动能量控制机理等方面的深刻认识。本文目的在于对仿生六足机器人的控制方法及运动规划进行研究，提出了一种基于A-Star算法 [12] [13] 的图表搜索 [14] [15] 步态生成方法，并对足端轨迹进行多项式拟合，从而实现山地环境的跃障能力。最后通过虚拟样机对机器人的运动规划进行仿真，并在机器人实物平台上对机器人的步态控制策略进行实验验证，为进一步研制大型重载六足仿生机器人打下理论的基础。

2. 六足机器人运动学分析

机器人运动学通过分析机器人的具体结构，来研究各个运动机构与机器人末端执行器件之间的关系 [16]。本文分析了山地重载机器人足端位置与各个关节转角之间的关系 [17]，求出其正逆运动学解，为后续的研究工作提供理论支持。

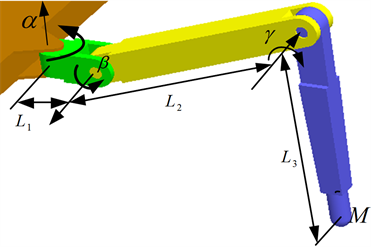
本论文研究对象为大型重载六足机器人，由机体与六条单腿组成，单腿对称分布于机体两侧。单腿结构包括基节、大腿、小腿和足端，基节和机体平台之间、大腿和基节之间、大腿和小腿之间均由销轴连接形成三个旋转副分别称为跟关节、髋关节、膝关节。为研究方便，暂不考虑足端的大小及形状，并假设机器人腿形状完全相同、左右完全对称。简化机器人的仿真模型如图1所示。

(a) Simplified structure of the whole machine(b) Diagram of single leg structure

Figure 1. Simulation model of simplified robot

图1. 简化机器人的仿真模型

设定基节长度L₁为300 mm，大腿长度L₂为1500 mm，小腿长度L₃为1500 mm，基关节角度α取值区间[−30˚, 30˚]，大腿关节角度β取值区间[−30˚, 45˚]，小腿关节角度γ取值区间[45˚, 100˚]。

2.1. 单腿正运动学解

以单腿基节根部为坐标原点，机体侧向前进方向为X轴，正向前进方向为Y轴，垂直于机体向上为Z轴建立直角坐标系O-XYZ，坐标系遵循右手定则。已知各关节转角α、β、γ，足端点 $\text{M}$ 在坐标系O-XYZ中足端坐标为 $\left(x_M,y_M,z_M\right)$，单腿坐标系下足端点位置如图2所示。

(a) XOZ coordinate system (b) XOY coordinate system

Figure 2. The position of the foot ends in a single leg coordinate system

图2. 单腿坐标系下足端点位置

出于实际应用的考虑，也为方便控制程序的编写，本文不采用常见的D-H变换矩阵 [18] 求解，而运用基础的几何学求解正运动方程与足端坐标。根据几何学关系，易得单腿正运动变换方程为：

$\{\begin{array}{l}{x}_M=\left[l_1+l_2\times \cos \beta +l_3\times \cos \left(\gamma -\beta \right)\right]\times \cos \alpha \\ y_M=\left[l_1+l_2\times \cos \beta +l_3\times \cos \left(\gamma -\beta \right)\right]\times \sin \alpha \\ z_M=l_2\times \sin \beta -l_3\times \sin \left(\gamma -\beta \right)\end{array}$ (1)

2.2. 单腿逆运动学解

六足机器人通过控制所有站立腿的驱动关节转动角度来实现前移，逆运动学分析是根据机器人位姿信息和已知的足端点坐标信息求解各个关节转角的过程，即已知足端坐标 $\left(x_M,y_M,z_M\right)$，求解各关节转角 $\left(\alpha 、\beta 、\gamma \right)$。由于本文采用的是简化的单腿模型，建立D-H坐标系进行矩阵变换求解过于繁琐，因此可用几何学方法进行逆运动学求解。

由于式(1)中给定了坐标 $\left(x_M,y_M,z_M\right)$，又l₁、l₂、l₃均为已知量，α、β、γ的取值范围已知，通过构造辅助线AM，结合ΔABM的正弦定理和余弦定理，即可求解各关节转角变量的值，整理如下：

$\{\begin{array}{l}\alpha =\arctan \left(\frac{y_m}{x_m}\right)-{30}^{\circ }<\alpha <{30}^{\circ }\hfill \\ \beta =\arcsin \left(\frac{l_3\times \sin \gamma }{l_{AM}}\right)+\arctan \left(\frac{z}{\frac{x}{\cos \alpha }-l_1}\right)-{30}^{\circ }<\beta <{45}^{\circ }\hfill \\ \gamma =\arccos \frac{l_{AM}^2-\left(l_1^2+l_2^2\right)}{2\times l_1\times l_2}{15}^{\circ }<\gamma <{100}^{\circ }\hfill \\ l_{AM}=\sqrt{{\left(\frac{x_m}{\cos \alpha }-l_1\right)}^2+{\left(z_m\right)}^2}\hfill \end{array}$ (2)

3. 六足机器人的运动规划与仿真实验

本文所研究的大型重载机器人工作于高山、丘陵等恶劣环境中，为保证机器人的稳定运动，同时具备跨越障碍物和沟壑的能力，需要对机器人进行运动规划分析。运动规划包括两个方面，分别是步态规划和足端轨迹规划。本文在给定行走步态的前提下，结合MATLAB规划设计了一套具有一定越障能力的足端轨迹，并利用运动学分析软件ADAMS进行了运动仿真验证。运动规划过程如图3所示。

Figure 3. Process of motion planning

图3. 运动规划过程

3.1. 步态规划

六足机器人是一种模仿节肢动物行走的机器人，通过对自然界的节肢动物进行研究发现，昆虫常见的三种步态 [19] 分别是二步态，三步态，六步态，这三种步态的区别在于在某时刻，支撑腿的数目分别是3、4、5。六足机器人步态类型主要取决于负载大小与路面环境，当负载越大、路况越复杂时，支撑腿数目越多，支撑时间越长，前进速度越慢，对控制系统的要求也越高。自由步态 [20] 没有固定的摆腿顺序，增强了对环境的适应能力，六足机器人在该状态下可由任一特殊姿态恢复到常规步态，在复杂地形环境中自由步态具有非常重要的意义。本文采用图表搜索法并结合所研究的六足机器人具体特性来生成自由步态。同时为了使步态快速收敛到常规步态并在收敛的过程中保持稳定性最好，采用A-Star算法作为优化算法，制定基于稳定性最优、恢复速度最优等优化策略，实现代价最小的自由步态生成机制。

3.1.1. 六足机器人支撑状态及转变

六足机器人腿的支撑状态用一个二进制数来表示，1代表着地，0代表摆动，整机支撑状态是一个二进制行向量，该向量由各个体腿的支撑状态构成，例如1、3、5号腿着地，支撑状态可以表示为(1 0 1 0 1 0)。六足机器人行走时，为保证稳定性，在同一时刻至少需有三条腿着地，共有 $C_6^3+C_6^4+C_6^5+C_6^6=42$ 种支撑状态。这42种支撑状态中，有一些状态不稳定，需要剔除。本文考虑六足机器人稳定性能，择优选择出一套有效的支撑状态。23种稳定支撑状态如图4所示。

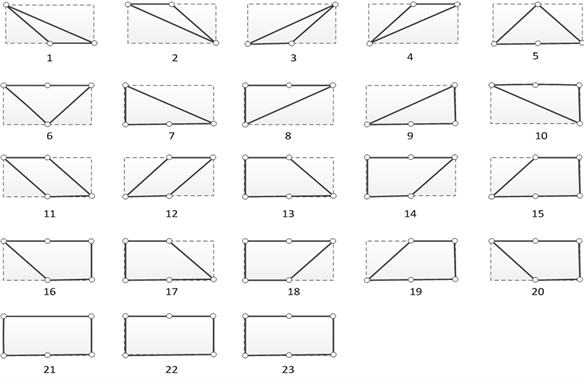
Figure 4. 23 kinds of supporting state forms of hexapod robot

图4. 六足机器人23种支撑状态形式

当六足机器人移动时，它切换了一系列的支撑状态，当六足机器人由支撑状态a转变到支撑状态b时，支撑状态b称为支撑状态a的连接状态。本文课题从六足机器人的稳定性考虑，规定在每次状态转换时仅仅有一条腿抬起或落下，建立了一种支撑状态转换表，如表1所示。

Table 1. Transition table of support state

表1. 支撑状态转换表

3.1.2. 基于A-Star算法的图表搜索步态生成法

图表搜索算法旨在生成每条腿的运动状态序列，图表中节点代表六足机器人某个时刻运动状态，根节点即初始状态，目标节点为目标状态。图表搜索原理即为从根节点扩展出子节点，从子节点中选出期望值最高的节点，再次进行扩展直到目标状态位置，从而得出一条最优路径，该路径即为六足机器人由特殊状态到常规步态的自由过渡步态。图表搜索的原理示意图如图5所示。

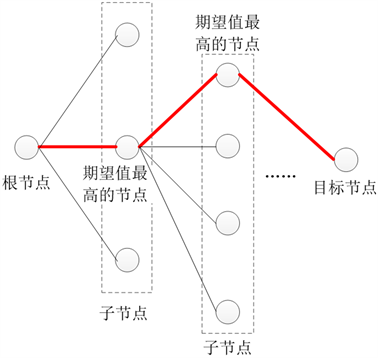
Figure 5. Schematic diagram of chart search

图5. 图表搜索的原理示意图

搜索过程中为减少图表搜索次数，实现快速稳定地收敛，本文采用启发式搜索规则和A-Star算法来限制节点数目及获取最优步态。启发式搜索包括三项规则，即当某条腿触地后需完成指定数目运动片段才能被考虑抬起；当某条腿抬起后需在空中保持指定数目运动片段才能被考虑放下；当触地的某条腿到达运动学极限后必须抬起。A-Star算法是一种基于启发式搜索的优化算法，它以代价最小目标规划出一条合理路径，算法的核心部分为估价函数的设计，其公式如下：

$f\left(n\right)=g\left(n\right)+h\left(n\right)$ (3)

式中 $f\left(n\right)$ 为节点n的估价函数， $g\left(n\right)$ 为根节点到当前节点的实际代价， $h\left(n\right)$ 为当前节点到目标节点最优路径的估计代价。

本文采用一种基于A-Star算法的图表搜索法实现六足机器人由特殊步态向常规步态的稳定过度。首先初始化搜索图表，将六足机器人的初始状态作为根节点r，将其放入开放列表中。从开放列表中选择出最优节点进行扩展，把扩展出的子节点再放到开放列表中，如果某个子节点是目标节点则认为获得可行的回归路径。基于A-Star算法的图表搜索流程如图6所示。

3.2. 六足机器人足端轨迹规划

大型重载六足机器人要求在复杂地形稳定行走、跨越障碍，这就要求对足端点运动轨迹合理规划。多项式拟合生成的足端轨迹曲线可以在特定的时间经过一系列特定的点，也可在特定位置满足特定的运动约束条件，比如越障、跨沟等，本文采用该方法对机器人模型进行足端轨迹拟合。

以机器人躯体为固定参考坐标系，处于摆动相的腿相对机体向前运动，支撑相的腿相对躯体向后运动。令足端轨迹高度为H，宽度为W，从后极限位置A到前极限位置C之间的轨迹曲线ABC为摆动腿足端轨迹，CA为支撑腿足端轨迹。单腿轨迹简化模型如图7所示。

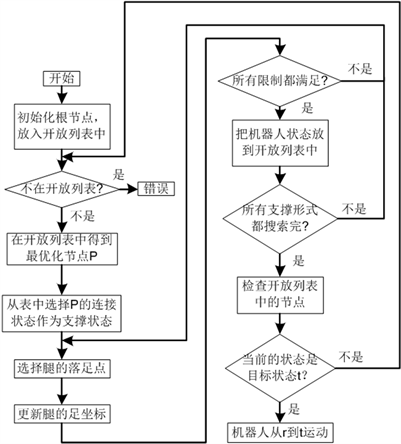
Figure 6. Graph search process based on A-Star algorithm

图6. 基于A-Star算法的图表搜索流程

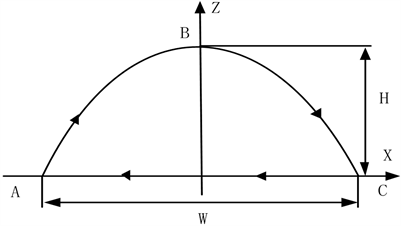
Figure 7. Curve model of simplified foot end trajectory

图7. 简化足端轨迹曲线模型

设机器人摆动过程所花总时间为t₂，到达最高点时间为t₁。给定A点位置、速度、加速度，B点位置，C点位置、速度、加速度信息，构成7个边界约束条件，由此可唯一确定关于时间t的6次多项式，该多项式曲线即为摆动足端的轨迹：

$p\left(t\right)={\displaystyle \underset{i=0}{\overset{6}{\sum }}{c}_i{t}^i}$ (3)

式中c_i为多项式中的常量，将7个边界约束条件代入(3)中构成含有未知量c_i的七元一次方程组，求解方程组即可得到c_i的值。

3.3. 运动仿真实验

六足机器人有三种典型步态，本文最初对二步态行走进行仿真实验。行走仿真周期设为2秒，六条腿分两组： $L1、R2、L3$ 和 $R1、L2、R3$，其中 $L1、L2、L3$ 为机器人左边1、2、3号腿， $R1、R2、R3$ 为机器人右边1、2、3号腿。每条腿进行支撑相和摆动相的交替切换，同一组腿运动轨迹相同，当一组腿作为摆动相向前摆动时，另一组腿作为支撑相向后扭腰，推动机器人前移。

采用Solidworks进行机器人三维建模，导入模型至ADAMS，该导入模型会保留几何形状，并自动建立关键点和全局坐标系。在ADAMS添加材料属性、约束条件与驱动，结合MATLAB生成的足端轨迹完成仿真实验，后根据逆运动学解可仿真得到各足关节角位移曲线。分析结果表明，在支撑相和摆动切换时刻(t = 0 s, t = 2 s, t = 4 s)机器人的关节速度和加速度均为零，说明每条足腿在支撑相和摆动相这两种相邻运动状态之间的过渡足够平滑稳定，步态切换或地形变化时，能有效减小足腿运动状态变化引起的抖振现象。机器人的足端轨迹曲线表明，其在运动过程中能够满足跨越指定尺寸障碍物的要求，不会产生干涉，并且可以通过实时调整足端轨迹高度和宽度等参数信息来应对不同大小的障碍物。六足机器人模型的ADAMS运动仿真过程表明，机器人仿真过程中的行走步态序列与本文的步态算法生成序列一致，说明本文提出的步态生成方法能够保证六足机器人的二步态或多步态稳定行走。机器人足端在各坐标轴的轨迹如图8所示，各足关节角位移曲线如图9所示，机器人各状态ADAMS运动仿真如图10所示。

(a) X-axis curve (b) Y-axis curve (c) Z-axis curve (d) Spatial variation curve

Figure 8. The trajectory of the robot's foot at each coordinate axis

图8. 机器人足端在各坐标轴的轨迹

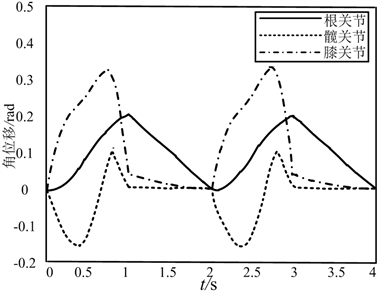
Figure 9. Simulation results of two-step single-leg joint

图9. 二步态单腿各关节仿真结果

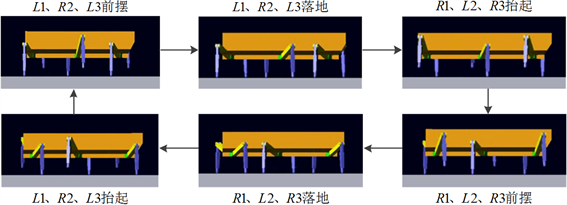
Figure 10. Two-gait simulation of a six-footed robot on the ground

图10. 六足机器人平地二步态仿真

4. 实物平台运动分析

为验证本文提出的行走步态策略、足端轨迹规划方法在实际工作中的可靠性，结合18自由度小六足机器人平台，进行直线二步态行走实验。六足仿生机器人主控芯片为ARM芯片LPC1114，ARM芯片通过串口连接上位机，发送PWM波到舵机，实现期望运动。机器人外形如图11所示。

Figure 11. Two-gait simulation of a six-footed robot on the ground

图11. 六足机器人平地二步态仿真

设置机器人足端轨迹高度H为3厘米，宽度W为2厘米。使用本文提出的基于A-Star算法的图表搜索步态生成方法，规划机器人在二步态模式下的支撑状态序列。后根据相邻支撑状态变化来分析各单腿的支撑相或摆动相动作类型，并结合本文提出的足端轨迹规划可以得到单腿轨迹曲线，再根据机器人的逆运动学解可得到各关节的转角，控制各舵机相应旋转，实现机器人的前行运动。

观察行走过程中机器人姿态变化，发现机器人行走平稳，支撑相至摆动相的过渡平滑，能实现二步态行走。为验证控制的准确性，设置目标位移值500 mm，测定机器人二步态行进的实际距离，重复三次。结果表明机器人平均向前移动了464.33 mm，误差为7.2%。初步分析，误差来源有两点：1) 行走过程中，支撑腿承受机器人重量会有一定的变形，使得舵机行进距离略小；2) 机器人行走时有一定滑移，导致实际行走距离比理论值小。在后期制作真实环境重载六足机器人时，将对机器人的整体刚性和防滑能力作出进一步的优化，以进一步提高运动精度。综合观察18自由度小六足机器人平台的运动情况可以看出，本文提出的行走策略和足端轨迹规划方法应用在实际六足机器人上时，能够保证运动的精确和平稳，具备一定的跃障能力，同时能够自行调整步态序列，适合在复杂的地形环境中行走运动。二步态机体前进位移结果如表2所示。

Table 2. Forward displacement of two-gait

表2. 二步态机体前进位移

5. 结论

本文提出一种基于A-Star算法的图表搜索步态生成方法，结合图表搜索法和A-Star优化算法的各自优势，实现六足机器人运动步态序列的快速生成，提高了系统稳定性和抗干扰性能。针对复杂环境的跃障需求，采用多项式拟合方法规划足端运动轨迹，通过调整轨迹高度、宽度相关参数即可灵活应对不同地形。运动仿真结果表明，单腿足端运动轨迹曲线平滑，支撑相和摆动相切换时关节速度、加速度均为零值，在山地环境行走时能有效减少控制型抖振现象。实物模型运动分析结果表明，本文算法在二步态机体行进中具有很好的稳定性，重复移动误差低，能有效应用于实际复杂环境。后期将采用真实重载六足机器人验证本文算法，并作出进一步的分析改进。