1. 引言
分类算法是机器学习的一个重要分支。传统的分类算法大多基于平衡的数据集,即假设不同类别间样例数目相对平衡,并且以总体分类准确率为分类器效能评价指标。然而,在诸多实践中,我们能够获取的数据集中不同类别的样例数往往是不平衡的。例如在病例诊断 [1] 中,多数样例为健康,仅有少数为患病;又如在信用评估 [2] 中,也仅有极少数的样例信用记录不良。当面对不平衡分类任务时,传统的算法会倾向于多数类,假设一个数据集中多数类与少数类的比例为99:1,即使将全部样例均预测为多数类,总体准确率依然可以高达99%。然而在不平衡分类中,更为重要的往往是识别少数类的能力,这使得接近于1的总体分类准确率并无意义。因此,提出针对不平衡数据的有效分类算法尤为重要,这也是近年分类算法研究的一个趋势。
本文从集成学习的角度出发,构建了一个基于Bagging框架的随机秩次k-近邻不平衡数据分类算法(Random Ensemble k-rank nearest neighbor Algorithm, REKRNN)。它将秩次k-近邻分类器(k-rank nearest neighbor,简称k-RNN)应用于集成学习框架中,使k-RNN学习能力强、算法复杂度低的优势,与Bagging的高泛化性能相结合,将重采样和分类算法嵌入推进,最终获得了良好的分类性能。
2. 相关研究
2.1. 不平衡数据分类的集成学习算法
近年来的国内外研究中,提高不平衡数据中少数类分类准确率问题的方法主要分为三个类别:数据层面,算法层面和集成学习。数据层面是指在训练模型之前,对原始数据集进行不同方式的重采样,调整多数类和少数类样本的个数,从而降低不平衡度。例如,通过上采样重复选取少数类样本 [3],或者通过降采样减少多数类样本 [4],来重构数据集使其中不同类别样本数目相对平衡。然而,预处理后用于最终训练分类器的单个数据集,会损失样例特征信息或重复采样多次而造成大量的信息浪费,因此数据层面的方法在不平衡率较高时不适用。算法层面是指针对不平衡数据的特点,提出新的分类算法或者对已有算法做出改变。例如代价敏感学习,通过为不同类别样本设置不同错分代价提高分类准确率。
集成学习是数据和算法的混合方法,它的主要思想是创建一系列弱学习器,再以一定的策略将其结合做出最终决策,利用弱学习器之间的差异性得到更全面的强分类模型。集成学习能够有效地将采样方法和分类算法嵌入推进,是效能更高的不平衡数据分类算法。其中Boosting类通过引入代价敏感学习更新权重,改变多数类和少数类样本的分布,串行生成分类器。它通常基于整个特征空间构建算法,因此整体复杂度较高,不利于高维数据处理。与之相比,Bagging类并行生成基分类器,算法结构更为简单,具有较高的泛化性能 [5] [6]。因此本文提出的REKRNN算法采用Bagging框架,构建以k-RNN为弱学习器的不平衡数据分类算法。
现有的基于Bagging的集成算法中,多数采用决策树作为弱学习器,例如随机森林。近年来,研究者将更多的机器学习算法引入其中,例如神经网络,支持向量机等,使得单个学习器的性能通过集成得到提升 [7]。然而,在特征数较多时,这些算法在学习过程中容易因为复杂度高而产生过拟合现象,使得模型整体泛化性能较差。同时,计算过程时间和资源消耗巨大。
为了降低运算成本,本文首次采用了模型复杂度更低的秩次k近邻算法(k-rank nearest neighbor classifier)作为集成算法的弱学习器。单变量的 -RNN规则首先由Anderson等人于1996年提出,随后Bagui和Pal进一步将之拓展为适用于多变量的分类算法 [8] [9]。与最为经典的k-NN算法相同,它的主要思想是如果一个样本在样本空间中的大多数“邻居”都属于一个类别,那这个样本也属于这个类别 [10]。在分类决策时,只依据这些邻居的类别来做出预测。所不同的是,在寻找最近邻样本时,k-NN基于每两个样本间的距离,而k-RNN基于对各个类别样本混合排序后的次序,即秩次。试验证明,k-RNN在拥有与k-NN相当的分类性能的同时,算法的复杂度更低。
2.2. k-RNN分类器
原始的k-RNN规则适用于单变量总体,即总体中样本仅有一个特征,它规则和主要思想如下:
设
和
是分别来自两个给定总体
和
的训练样本集,测试样例Z可被分类至总体
或
。将X,Y和Z全部样本(
个)按照降序(或升序)排列,得到混合样本的秩次;然后,取Z左边的样本和右边的样本各k个作为秩次最近邻,样例Z的预测类别将由这2k个最近邻中的出现次数较多的类别标记为预测结果。
尽管原始的k-RNN规则有很好的分类能力,但由于“按照降序(或升序)排列”这一概念无法自然地扩展到多变量总体,它只能用于单一特征的总体分类任务。为了将k-RNN规则能够适用于多特征总体分类,并使其在大多数现实问题中得到应用,Bagui扩展了该算法,将Randlest的多维样本排序法引入其中,提出了基于排序的多元k-RNN分类器。该排序法综合了不同总体间的均值和协方差矩阵的差异,更加具有统计学意义。多元k-RNN分类器的主要思想如下:
设
和
是分别来自两个给定总体
和
的训练样本集。其中
,总体均值为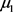 ,协方差矩阵为
;
,总体均值为
,协方差矩阵为
。测试样例
可被分类至总体
或
。基于原始k-RNN规则,测试样例Z在多维样本X,Y和Z中的混合秩次由以下得分函数获得:
,协方差矩阵为
;
,总体均值为
,协方差矩阵为
。测试样例
可被分类至总体
或
。基于原始k-RNN规则,测试样例Z在多维样本X,Y和Z中的混合秩次由以下得分函数获得:
(1)
其中,
表示均值向量
的转置,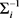 表示协方差矩阵
的逆矩阵。
表示协方差矩阵
的逆矩阵。
在大多数的应用环境中,参数
和
均为未知。Johnson等人证明,可以由它们的无偏估计
和
代替得到得分函数的无偏估计:
(2)
其中,
(3)
(4)
更进一步地,Bagui和Pal利用大数定律证明了
。即得分函数的估计值
依概率收敛到
[8]。
由此可知,得分函数
或者
是一个从
到
,从p维到1维的映射,它的得分值代表了任一样例在X,Y样本集中的混合秩次。通过得分函数计算X,Y中每个样例的分值,就能够得到混合样本中全部样例的秩次。原始k-RNN规则中排序得到秩次的思想通过得分函数得以解决,使之可以成功应用于多特征分类任务中,依据秩次选择双侧最近邻进行样例的分类预测。
多元k-RNN分类器的训练过程如下表1:

Table 1. k-RNN classifier algorithm
表1. k-RNN分类器训练过程
3. 随机秩次k-近邻集成学习算法
3.1. Bagging算法
Bagging是一种典型的集成学习算法,是当前机器学习算法研究的热点之一,在分类和回归任务中都有广泛的应用和良好的效果。它的实现步骤为:每次从训练集中有放回地抽取n个样本,重复抽取T次;由这T个样本各训练一个弱学习器;由T个弱学习器各对测试样本进行预测,按照投票取众数的方法得到最终预测结果。其中重要的步骤有放回抽样,即为Bootstrap抽样,Bagging名称的来源。它的主要思想是通过弱分类器之间的差异性提高模型泛化性能。针对不平衡数据分类的任务,REKRNN算法对Bagging框架做出如下改进:1) 采用混合重采样法对初始训练集进行采样以获得较为平衡的训练集;2) 引入随机特征子集降低维度和计算复杂度。
3.2. 混合重采样
弱分类器间的差异首先通过重采样得到不同的训练子集获得。在Bagging中,通常由Bootstrap实现重采样过程,即从初始训练集(样本容量为N)中有放回地随机抽取同等数量的样本(N个)形成训练子集。可以证明初始训练集中约63.2%的样本会被选入训练集中,且其中一些样本重复出现。
而针对不平衡数据集,Bootstrap并不会对多数类和少数类样本有任何偏好,依然均衡地进行有放回抽样。因此重采样后的样本子集仍然为不平衡数据集,且当总样本量小或不平衡率很高时,有极大可能Bootstrap子集中没有少数类样本或样本过少影响分类算法的学习。同时,由于REKRNN中弱分类器的算法 -RNN仍然以类别间相对平衡为前提,因此仅仅对少数类获取Bootstrap样本,而对多数类采用降采样随机抽取与少数类相同数目的样本,由此得到少数类数目相对稳定且类别间相对平衡的数据集。
3.3. 随机特征子集
第二个获得弱分类器差异的方法为随机特征子集,即创建若分类器时仅以特征空间的一个子集为分类依据。例如在随机森林中,每棵决策树的节点不是在整个特征空间中进行搜索,而是在一个随机产生的特征子集中选择最优分裂 [11]。与此类似,REKRNN算法在每一个重采样的样本子集上,随机选择不同的特征子集训练弱分类器,保证弱分类器的多样性,增强整体算法的泛化性能。另一方面,随机选择子集可以降低特征维度,在高维数据分类中能够有效提高算法效率。同时,多个子集集成也可以弥补降维带来的潜在精度损失。随机特征子集的选择过程如下表2:

Table 2. Random feature space algorithm
表2. 随机特征子空间算法
3.4. 训练及测试过程
随机秩次k-近邻集成学习算法(REKRNN)将秩次k-近邻分类器k-RNN应用于Bagging集成学习框架中,将k-RNN分类器学习能力强、算法复杂度低的优势,与Bagging算法随机样本空间、随机特征空间分割集成的优势相结合。同时,对该框架加以改进,针对多数类样本采用降采样,针对少数类样本采用Bootstrap重复采样,以获得更加平衡的训练集,有效地提高数据集不平衡时的分类性能。
REKRNN算法的实现主要有四个过程,如图1所示:
1) 按一定比例将数据集划分为测试集和训练集,利用混合重采样法,对少数类样本取Bootstrap样本,多数类进行降采样,从训练集中抽取样本生成r个训练子集;
2) 针对每个训练子集,随机选择将采用的特征数,在特征空间中随机抽取特征子集,生成最终训练样本;
3) 在每个训练样本子集上建立k-RNN弱分类器;
4) 由弱分类器预测测试样本类别,使用“投票法”,将多数弱分类器的预测结果标记为最终分类结果。
4. 实验与结果分析
4.1. 实验数据集
1http://www.keel.es/
为了验证REKRNN算法对于不平衡数据集的分类性能,以及对少数类样本的识别能力,本文选取KEEL1中Abalone9-18数据集进行仿真实验。该数据集含有731个样本的8个特征,其中多数类样例684个,少数类样例仅有42个,不平衡率(多数类/少数类数目)高达16.68,是一个典型的不平衡分类数据集。
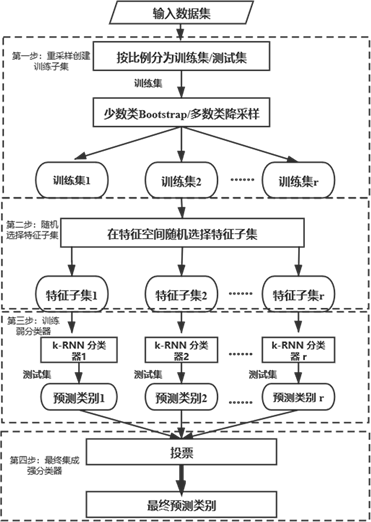
Figure 1. REKRNN algorithm flow chart
图1. REKRNN算法流程图
4.2. 评价指标
定义实验数据集中少数类样本数为P,多数类样本为N,相对应的混淆矩如表3所示:
依据混淆矩阵,总体精确度(Overall accuracy)为分类正确的样例数占总样例数的比例:
(5)
敏感度(Sensitivity),或查全率(Recall)为被预测为少数类的样例中真正少数类的比例:
(6)
特异性(Specificity),或查准率为实际类别为多数类的样例中也被预测为多数类的比例:
(7)
F值(F-measure),是对敏感度和特异性的折中:
(8)
ROC曲线是对敏感度和特异性的综合图示,AUC (area under ROC curve),即ROC曲线下的面积,经常作为一种不平衡分类的评价指标。
4.3. 实验过程与结果分析
为了验证REKRNN算法的分类性能,以及过程中使用的混合重采样,随即子空间两种技术对于提升学习器k-RNN算法分类性能的效果,分别使用单个基础k-RNN算法,重采样后平衡数据集的k-RNN算法,以及最终形成的REKRNN算法进行仿真实验。同时,以KNN和Adaboost两种模型为参照,比较REKRNN算法的分类效果。
本文使用Python进行仿真实验。k-RNN和KNN中参数k,Adaboost中决策树的数目均由十折交叉验证获得。对于数据集的划分均采用训练集70%,测试集30%的分类比例。以上文提到的五种评价指标为分类效果准则,结果均用百分数表示。实验结果见表4。
由上表,我们可以看出,在单个k-RNN分类的基础上,使用混合重采样得到平衡数据集后算法的查全率,F值和AUC分别提高了55.36%,33.51%和20.06%,这表明重采样使得算法对于少数类样本的分类能力大大提升;在此基础上,加入Bagging和随机子空间法后,使用REKRNN模型后查准率,F值和AUC又分别提高了8.9%,4.7%,4.45%,这表明通过集成和随机特征选择又进一步提高了模型的泛化能力。同时,与Adaboost和KNN算法相比,本文提出的REKRNN算法在各个指标下均表现更优,表明此算法在不平衡数据分类中具有良好的表现。
5. 结论与展望
针对不平衡分类任务中少数类样本分类准确率低的问题,本文提出基于随机秩次K近邻规则的不平衡数据分类算法——REKRNN。k-RNN分类能力强,算法复杂度低,Bagging集成框架提高算法整体泛化性能,混合重采样使得子训练集相对平衡,随即子空间算法降低维度的同时增大基学习器差异性。从仿真实验结果来看,这四个元素均对少数类分类准确率的提高有很大贡献,使得算法能够有效识别少数类样例。与两种传统分类算法相比,REKRNN也体现了它在不平衡数据分类中的优势。在下一步的研究中,可以考虑将代价敏感学习引入算法中,通过为少数类样例设置较大错分代价提高其分类准确率,进一步提高算法分类性能。
NOTES
*通讯作者。