1. 引言
数据挖掘是从大量数据中挖掘有趣模式和知识的过程,聚类分析是数据挖掘的一种重要技术手段,它将一个数据集对象或观测划分成若干子集 [1]。K-Means算法是聚类分析中一种基于划分的无监督学习算法。具有思想简单、效果好、容易实现的优点,广泛应用于机器学习等领域 [2]。但其对初始中心敏感、易陷入局部最优等问题也是近年来研究者对此算法进行改进的重点。文献 [3] [4] [5] [6] [7] 采用改进群体智能等方法与K-Means混合聚类以及从优化初始中心的角度考虑改进K-Means。人工蜂群算法(ABC)因其搜索速度较快、鲁棒性好、且易于实现的优点被广泛应用。但由于搜索策略的局限性,人工蜂群算法虽然在前期性能较好,但在后期易陷入局部解。文献 [8] [9] [10] 对于ABC算法的问题进行改进,优化蜂群的搜索策略,但算法的收敛速度偏慢。文献 [11] 将人工蜂群算法改进后与K-Means算法相结合,一定程度提高了聚类质量,但是该算法随机产生食物源,降低了种群的多样性。文献 [12] 为避免聚类中心可能是同类样本而采用最大最小距离积法产生初始聚类中心。本文提出了一种结合人工蜂群与K-Means的改进混合聚类算法,IGABC-K-Means++算法,降低了初始聚类中心的依赖性和陷入局部最优解的可能性,有效提高了算法的聚类效果和稳定性,缩短了聚类时间。
2. 相关算法简介
2.1. 原始K-Means算法
设样本集为
,其中
(
),现将这N个D维的数据聚类:
Step 1:随机选取k个簇中心点;
Step 2:遍历所有数据,将每个数据划分到欧式距离最近的中心点中;
Step 3:计算每个聚类的平均值,并作为新的簇中心点;
Step 4:重复2~3,直到某个中止条件。
2.2. 人工蜂群算法
人工蜂群算法具体实现步骤:
Step1:初始化蜂群数NP、食物源个数SN,最大迭代次数MCN、食物源停滞的最大次数Limit和确定搜索空间D,通常有SN = NP/2;在设置的区间内按照公式(1)随机生成SN个食物源并根据公式(2)计算其适应度值fitness。
;
(1)
(2)
公式(1)中,
表示
之间分布均匀的随机数。aj和bj分别表示第j维数据的上限和下限(
)。
Step2:引领蜂由式(3)进行邻域搜索,产生一个候选食物源并计算fitness,
(3)
公式(3)中,
;Rij为
之间的随机数。对比新解与旧解的fitness,如果新解较好,就用新解取代旧解,否则,仍用旧解,同时将食物源的停滞次数加1。
Step3:跟随蜂按照轮盘赌选择引领蜂,根据公式(3)更新当前位置,fitness较大,被更新的可能越大,选择概率为公式(4):
;
(4)
Step4:经过Limit次循环后某个解没有被更新,则放弃当前食物源,此引领蜂转成侦查蜂。
Step5:完成MCN次迭代后,输出fitmax的最优解。
3. 一种基于人工蜂群与K-Means的改进混合聚类算法(IGABC-K-Means++)
3.1. K-Means++算法
为了解决因为初始化带来的K-Means算法的问题,K-Means++算法主要是让随机选取的中心点不再趋于局部最优解,而是让其尽可能的趋于全局最优解,解决K-Means算法的初始化问题。算法中,并不是直接选择距离最远的点作为新的簇中心,只是让这样的点被选做簇中心的概率更大。
具体步骤如下:
Step 1:随机寻找一个点作为中心点;
Step 2:计算其他点到目前的全部簇中心点的距离(最开始只有一个中心点);
Step 3:利用公式(5)计算出映射到对应点的概率。
(5)
其中D(k)就是第k个点到其他中心点的最短距离。
Step 4:根据Step 3中计算出的概率利用轮盘法随机选择出一个中心点,然后重复步骤2,3,4,直至找到全部中心点。
3.2. 适应度函数设计
适应度函数的选取是影响算法稳定性和收敛性的关键因素 [1],本文结合人工蜂群迭代搜索过程以及K-Means算法思想提出一种新的适应度函数,如式(6)所示。
(6)
表示第j类的类内距。CNj表示属于第j类的样本数。
如果仅以类内距作为适应度函数,就会忽略类内样本数对于类内离散度的影响。当各类样本数目差距较大时,仅仅用类内距作为适应度函数是不合理的,本文将平均类内距离作为适应度函数。Fitness值越小,表示类内离散度越小,类内点密度越大,说明粒子的位置越好,聚类结果也就越精确。
3.3. GABC算法
朱国普等学者提出了全局最优解引导的ABC算法(GABC算法) [13] [14],该算法在位置搜索公式中添加了全局最优项来指导算法的搜索过程,通过添加全局最优项来加强算法在全局最优解附近的搜索能力而且收敛速度也有所增加 [15]。使用公式(7)取代原始ABC算法中的公式(3)。
(7)
Rij是
中的一个随机数,xbest表示全局最优食物源,
是
(C是一个正数)中的一个随机数,经多次实验,当
时效果最好。
3.4. 贪婪选择
在原始人工蜂群算法中,跟随蜂按照轮盘赌选择引领蜂时,适应度值越大,被搜索到的概率越大。在本文中,将跟随蜂的选择概率定为公式(8):
,
(8)
适应度值越小表示引领蜂的位置越好,被选择的概率越大。
3.5. IGABC-K-Means++算法的实现
本文将改进的全局人工蜂群算法与K-Means++算法相结合,提出一种新的混合聚类方法,算法描述如下:
Step 1:模型开始,设置引领蜂、跟随蜂的数量(一般情况下,二者相等);最大迭代次数MCN及控制参数Limit;聚类簇数K,Cycle = 1;利用K-Means++初始化SN个蜂群。
Step 2:对初始蜂群进行聚类划分,根据公式(6)计算每只蜜蜂的fitness,将值较小的50%为引领蜂,值较大的50%为跟随蜂。
Step 3:引领蜂利用式(7)进行邻域搜索,得到新位置,对比两个位置的fitness,按照贪婪选择原则,如果fit新 < fit旧,则新位置取代原位置;否则,保持原位置。并且将食物源的停止次数加1;当所有引领蜂完成邻域搜索后,根据式(8)计算概率Pi。
Step 4:跟随蜂利用Pi并基于轮盘赌原则选择引领蜂。当跟随蜂完成选择后,利用式(7)对邻域进行搜索,同样按照贪婪选择原则选择fiti小的位置。
Step 5:跟随蜂搜索结束,用K-Means对得到的位置进行聚类划分,更新蜂群。
Step 6:如果某引领蜂在Limit次迭代后,结果都没有改变,则变为侦察蜂,并随机产生一个新食物源。
Step 7:如果当前迭代次数达到最大次数MCN转向步骤8,否则转向步骤3,Cycle = Cycle + 1。
Step 8:输出聚类中心和对应的fitness,算法结束。算法流程图如图1所示:

Figure 1. IGABC-K-Means++ algorithm flowchart
图1. IGABC-K-Means++算法流程图
4. 实验结果及分析
4.1. IGABC算法性能测试
在函数优化时,设IGABC算法和原始ABC算法的种群个数NP = 20,SN = 10,Limit = 100,MCN = 2000。两种算法分别在Sphere、Griewank两个标准测试函数上进行性能测试,测试函数属性如下:
Griewank函数:
Sphere函数:
其中Sphere是单峰函数,Griewank是多峰函数,用适应度来评价改进算法的性能,得出结果如图2和图3所示。
结果分析:
从图2和图3可以看出原始ABC算法在两种测试函数上表现出了容易陷入局部最优并且有不同程度的收敛速度变慢的问题;IGABC在适应度函数和全局引导因子的作用下,迭代次数更少,可以找到的位置更优。
4.2. IGABC-K-Means++算法性能测试
为了验证IGABC-K-Means++聚类算法的有效性,实验选取UCI机器学习数据库中著名的Wine数据集和Balance-scale数据集,数据集属性如表1所示。算法参数设置:最大迭代次数MCN = 100;食物源个数SN = 10;食物源停滞的最大次数Limit = 100。
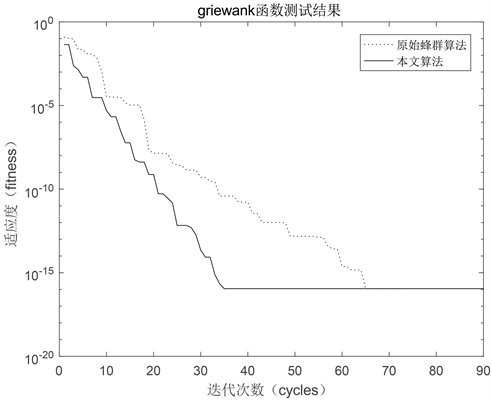
Figure 2. Fitness change of different algorithms in the Griewank function
图2. 不同算法在Griewank函数的适应度变化图
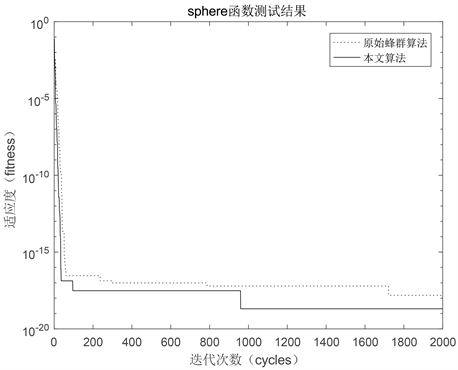
Figure 3. Fitness change of different algorithms in sphere function
图3. 不同算法在Sphere函数的适应度变化图

Table 1. Data sets used in the experiment
表1. 实验中使用的数据集
实验的软件环境Matlab2016b,Windows10操作系统。在相同的数据集下,都进行了20次的单独实验,取平均值,在收敛时间、最大值、最小值、平均值、标准差5个方面进行比较,结果如表2、表3所示:

Table 2. Clustering comparison results of wine data
表2. Wine数据聚类对比结果

Table 3. Cluster comparison results of Balance-Scale data
表3. Balance-Scale数据聚类对比结果
结果分析:
在表2和表3中可以看出,K-Means算法聚类耗时短但结果的标准差较大,每次实验结果差距较大,主要是由于初始聚类中心的影响,所以效果并不理想;
ABC+K-Means算法是把原始的ABC算法与传统的算法融合在一起,想比较而言,此算法的寻优能力比传统K-Means算法好一些,标准差减小,但ABC算法易早熟的问题仍然存在,所以算法后期收敛速度缓慢,需要消耗的时间更长;
IABC-K-Means算法是文献 [12] 提出的算法,采用最大最小距离积法产生初始聚类中心,克服了传统K-Means鲁棒性较差的缺点,聚类效果得到改善;
IGABC-K-Means++算法在选择的初始点时可以更好的反映数据实际分布,既保证了聚类准确度和算法效率,而且算法表现出很好的稳定性。
5. 结论
本文将改进的人工蜂群算法与K-Means++算法结合,从优化聚类中心位置入手,从蜂群的初始化、适应度函数、位置更新,贪婪选择四个方面进行改进以较大概率跳出局部极值,寻找更优的聚类中心,解决了K-Means算法全局搜索能力差的问题。实验对比结果表明IGABC-K-Means++算法效率改善的较为明显、性能也得到较大提高,优化了K-Means聚类效果和决策分析的准确度。下一步的研究目标是,利用改进的全局人工蜂群算法和K-Means++算法结合的混合聚类算法优势,将其应用于植物叶片高光谱图像数据中,研究融合算法的实用性。
基金项目
国家自然科学基金(No. 61962048, No. 61562067)。
NOTES
*通讯作者。