1. 引言
在进行岩土边坡、地下隧道、地基基础、水电站大坝安全评估分析中,往往需要计算结构的应力场和变形场。有限元数值计算模拟方法为精确定量描述结构的应力分布提供了强有力的计算手段。当计算模型材料的本构模型确定之后,如何客观准确确定估计材料的本构模型参数是极为重要的。无论有限元数值计算方法多么精确,如果材料力学模型参数估计不准确,所得到的计算结果也无任何工程意义。Tarantola指出,最小二乘法是求解模型参数估计问题最普遍、最简易的方法,其缺点在于该方法缺少鲁棒性,也就是对观测数据的误差及其敏感,也就是反问题解的稳定性问题 [1]。为了得到改性沙土的Duncan-Chang弹性非线性本构模型参数,Li采用遗传算法、基于不同围压条件下沙土三轴压缩应力–应变曲线,得到了沙土的力学模型参数 [2]。李守巨采用经典BP神经网络,基于堆石料的三轴压缩实验曲线,进行了堆石料本构模型模型参数估计研究 [3]。经典BP神经网络的缺陷在于泛化能力较差、其目标函数往往可能搜索到局部极小值,而不是全局最小值。为了解决这些问题,Lecun (2015)提出了深度学习神经网络模型,对神经网络的发展做出了创新性贡献 [4]。深度学习神经网络是重叠了许多隐含层的一种神经网络,使得其具有更好的学习泛化能力。卷积神经网络是深度学习神经网络中的一个典型代表,其隐含层是由多个卷积层和隐含层组成的。山下隆义深入讨论了深度学习神经网络输入数据的预处理方法和提高神经网络泛化能力的方法 [5]。涌井良幸推导了深度学习神经网络的权值计算数学模型 [6]。斋藤康毅基于Python理论,深入研究了深度学习神经网络的算法和程序实现 [7]。Chun基于卷积神经网络、采用数值模拟方法研究了锂电池电化学模型参数估计问题 [8]。Shen基于深度学习神经网络研究了锂电池电化学模型参数在线估计问题 [9]。Kazim基于深度学习神经网络研究了太阳能辐射模型参数估计问题 [10]。本文的目的在于讨论基于经典BP神经网络的参数反演方法的基本框架和算法。总结基于经典BP神经网络进行模型参数估计的主要步骤。分析经典BP神经网络所存在的某些缺陷及其改进方法。介绍基于深度学习神经网络估计模型参数的基本思路。讨论了深度学习神经网络超参数确定方法。
2. 经典BP神经网络在力学模型参数估计中应用
在岩土工程数值模拟分析中,首先需要确定岩土材料本构模型中的力学参数,经典BP神经网络某些为解决这些问题提供了强有力的技术手段。岩土材料是一种典型的非线性变形材料,其常用的岩土本构模型包括剑桥粘土模型(Cam-Clay),此模型非常适用于正常固结粘土和弱固结粘土。Duncan-Chang双曲线模型是一种非线性弹性模型,包括E-B模型和E-µ模型。Lade-Duncan弹塑性模型是根据对砂土的真三轴试验结果,提出的适用于表征砂土类的真三轴压缩实验数据。清华弹塑性模型是另一种弹塑性模型。基于Janbu (1963)提出的经验公式,采用Mohr-Coulomb破坏准则,Duncan和Chang (1970)提出一个土体非线性双曲线本构模型,即著名的Duncan-Chang弹性非线性本构模型,与围压和土体抗剪指标相关的土体切线模量为:
(1)
式中c为土体的粘聚力,
为土体的内摩擦角,Rf为破坏比,Pa是用与
和Ei相同的单位表示的大气压强,K、n为由实验确定的常数。因此,被估计的与土体变形模量相关的参数有5个,即K,n,Rf,c,
,5个参数。土体非线性弹性本构模型中含有两个独立的变量,一般经常采用切线弹性模量和和切线泊松比进行表征。因此,土体的另一个参数就是切线泊松比,它也是围压的函数。1980年Duncan通过用切线体积模量代替切线泊松比,提出了E-B模型:
(2)
与土体切线体积模量相关的参数有2个,即m,Rb,它们也是由实验确定。这样,与Duncan-Chang双曲线模型相关的被估计参数一共有7个。
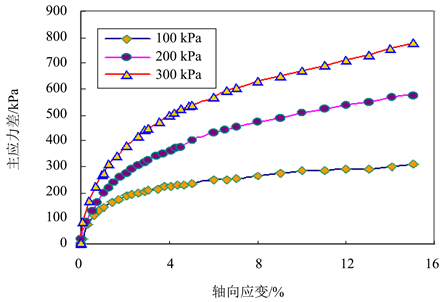
Figure 1. Relationship between stress and axial strain in different confined pressure
图1. 不同围压条件下沙土三轴压缩应力–应变曲线
改性沙土在不同围压条件下三轴压缩应力–应变实验曲线、三轴压缩径向应变–轴向应变曲线,如图1和图2所示 [2]。这两组曲线是进行沙土Duncan-Chang弹性非线性本构模型参数估计的基础。
基于图1和图2的沙土应力和应变观测数据,建立了如图3所示的神经网络模型,用于反演估计沙土的Duncan-Chang弹性非线性本构模型中的7个参数。其中,神经网络输入层神经元的个数与图1和图2离散点的个数相一致,
。隐含层神经元的个数取为
个,隐含层神经元的作用函数采用Sigmoid函数。输出层神经元的个数与被估计力学模型参数的个数相一致,
。输出层神经元的作用函数采用线性函数。
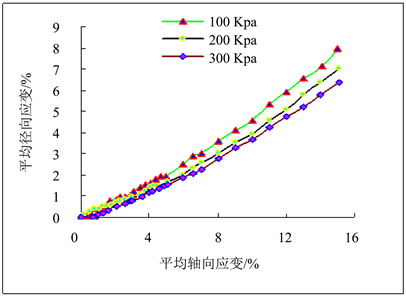
Figure 2. Relationship between radial and axial strains in different confined pressure
图2. 不同围压条件下沙土三轴压缩径向应变–轴向应变曲线
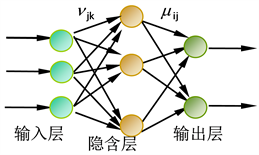
Figure 3. Topology structure of BP neural network for estimating model parameters
图3. BP神经网络的拓扑结构
基于前人已有的关于沙土力学模型参数研究的先验信息,初步估计Duncan-Chang本构模型中的7个参数可能的区间范围。采用MATLAB软件,基于沙土的Duncan-Chang弹性非线性本构模型,以主应力差和轴向应变增量形式给出,随机建立了90个训练样本,即神经网络样本集;10个测试样本,即测试集。建立训练样本时可以认为,力学模型参数在可能区间符合均匀分布或者状态分布。神经网络训练时,定义如下均方误差(mean squared error)为目标函数
(3)
式中
和
分别为神经网络输出层单元的实际输出和期望输出,P是训练样本的数目。在神经网络模型中经常采用的作用函数,包括Sigmoid作用函数
(4)
式中Sigma表示神经元的输入求和,f表示神经元的输出。
ReLU作用函数:深度学习神经网络除了传统的sigmoid函数之外,使用了RELU (Rectified Linear Unit)函数。当输入大于0时,该函数的输出就是输入;而当输入小于0时,该函数的输出是0。
(5)
双曲正切函数(Tanh)作用函数
(6)
线性作用函数
(7)
输出层神经网络任意神经元的输出表示为
(8)
式中mij为连接隐含层与输出层的权值;li为输出层的阈值,fo为输出层神经元的作用函数;z为隐含层的输出,Nh为隐含层神经元的个数。隐含层任意神经元的输出表示为
(9)
式中vjk为连接隐含层与输入层的权值;xk为隐含层的阈值,fh为隐含层神经元的作用函数。基于经典BP神经网络进行模型参数估计的步骤如下:
1) 基于先验信息,确定被估计力学模型参数的大致范围;随机产生训练样本集和测试集。当采用sigmoid作用函数时,输入数据需要进行归一化处理。输入数据的正规化(归一化normalization)处理,使得输入数据的值介于[−1,1]之间。
(10)
式中xkn为归一化后的神经网络输入。
2) 基于Duncan-Chang弹性非线性本构模型,确定将要模拟的围压值,解析计算在不同力学模型参数随机组合条件下的应力–应变曲线,类似于图1和图2;
(11)
式中
为偏应力增量,
为轴向应变增量。径向应变增量与轴向应变的关系为
(12)
式中
为径向应变增量。
3) 建立BP神经网络模型,确定神经网络的拓扑结构,随机给神经网络权值和阈值赋初始值,设定神经网络收敛准则;
4) 将训练样本集中应力–应变数据作为神经网络的输入,而力学模型中的参数作为神经网络的期望输出。基于MATLAB软件或者其他软件平台,采用优化方法训练神经网络,例如Levenberg-Marquardt优化算法,Quasi-Newton优化算法,直至神经网络收敛,记录神经网络的权值和阈值;
5) 将测试集输入到已经训练好的神经网络,检验神经网络的泛化能力和预测精度。
6) 室内进行土体三轴压缩实验,记录不同围压条件下的应力–应变曲线。将这些观测数据代入到训练好的神经网络模型,神经网络的输出就是力学模型的参数,具体的实施步骤和方法详见参考文献 [3]。
尽管经典BP神经网络在模型参数估计问题中得到了广泛的应用,但是其存在着许多固有的缺陷。其一,目标函数可能无法收敛到全局最优解。根据神经网络目标函数的定义可以看出,实际上,神经网络目标函数寻优过程,就是一个关于权值极小化的广义最小二乘法。基于梯度下降法的神经网络训练学习过程,无法避开局部极小值问题。其二,超参数的选取方法缺少理论依据。其三,隐含层的层数和单元个数确定缺少理论依据。其四,较差的神经元之间初始权值,可能无法得到理想的结果。其五,在某些情况下,会出现梯度消失问题,无法继续进行迭代。
3. 深度学习神经网络在模型参数估计中应用
卷积学习神经网络模拟了生物的视觉功能,是一类包含卷积计算,具有深度结构的前馈神经网络,采用有监督和非监督学习方法完成网络的学习训练,利用逐层推理方法实现自我学习和推理的功能,克服深层结构训练学习的困难 [4]。卷积神经网络是深度神经网络的一个典型代表。深度神经网络已经被广泛应用于科学建模 [11]、模型参数估计 [12]、时变系统的荷载参数识别 [13]、工业产品特征提取 [14]、故障诊断 [15] 等工程领域。卷积神经网络主要是针对于二维图像识别而开发的,它的输入常常是二维图片。而岩土材料力学模型参数估计用到的数据是主应力差随轴向应变变化的一维数据系列,如图1和图4所示。因此,需要研究一维卷积神经网络的特性和处理方法。金列俊基于一维卷积神经网络模型,提出了钻杆故障诊断方法,实验验证了所提出方法的有效性、适应性和抗噪能力 [16]。朱锡祥开发了基于一维卷积神经网络的辨识方法,用于车载语音识别研究 [17],韩林洁研究了基于一维卷积神经网络预测模型,进行轴承剩余寿命预测,并且进行了实验验证 [18]。
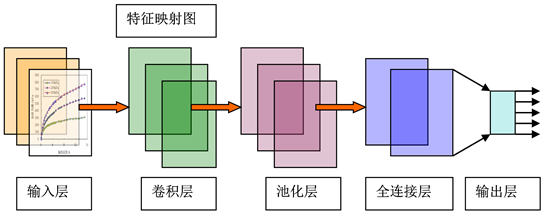
Figure 4. Topology structure of convolutional neural network for estimating model parameters
图4. 用于模型参数估计的卷积神经网络的拓扑结构
如图4所示,用于模型参数估计的卷积神经网络包括输入层、卷积层、池化层、全连接层和输出层组成。卷积神经网络是通过模仿动物或者人类的视觉原理来实现图像分类、识别的目的。其中,输入层输入的是多个图像信息,例如一幅256 × 256像素的图像。输入层可以处理多维数据,例如一维数组的时间序列,平面上的二位像素点。卷积层可以看作为输入样本与卷积核的内积运算,它应用了一个核函数,然后,经过作用函数计算后,得到特征映射图。卷积神经网络常用的作用函数包括sigmoid、tanh、ReLU等。卷积不是将函数作用在整个图像上,而是一次扫描图像的一个小窗口。卷积核的功能是对输入数据进行特征提取。池化层的作用在于减少卷积层产生特征图的尺寸。常用的池化方法包括,最大池化、平均池化以及LP池化。其中,LP池化是通过突出图像区域内的中央值而计算出新的特征图。最大值池化操作是在扫描区域中从每个通道中选取最大值。平均值池化操作使用平均值代替整个扫描区域。全连接层与多层感知器类似,通过作用函数计算出全连接层各单元的输出值。全连接层的作用是对提取的特征进行非线性回归,并传递给输出层。其输出层与经典的BP神经网络类似,通过作用函数计算出输出层各单元的输出值,输出层神经元的数目与被估计模型参数的数目相一致。
基于卷积神经网络模型,Chun用于锂电池电化学模型参数估计的训练数据包括:电池电压–时间曲线、电池电流–时间曲线、电池温度–时间曲线和SOC (state of charge)数据,这些数据都是基于锂电池正演计算模型(P2D, pseudo two-dimensional)得到的,数据的采样时间持续100 s,它们是待估计锂电池电化学模型参数的函数,被估计的P2D模型参数一共6个。训练样本数目72,000,测试样本数目1728。研究表明,模型参数的估计最大相对误差12.25%,最小的相对误差2.214% [8]。Shen研究了基于卷积神经网络模型锂电池电化学模型参数估计方法,目标函数采用了带有罚函数的正则化形式,训练数据包括:电池电压–时间曲线、电池电流–时间曲线、电池蓄电量–时间曲线。锂电池充电(放电)时间离散为25个时间步。Shen所建立的用于锂电池电化学模型参数估计的卷积神经网络共有28,000个参数,6000个神经元,包括5个卷积层,3个全连接层。Shen设定的卷积神经网络超参数值如下:动量项系数0.9,学习率0.01,目标函数中带有惩罚项网络权值正则化因子0.0001。数据中70%用作训练样本,30%用作测试样本。研究表明,预测的电池蓄电量最大相对误差3.52% [9]。
以图1所示的应力–应变曲线,在围压200 KPa时的一段数据作为卷积神经网络输入数据为例,讨论如何进行力学模型参数反演中卷积神经网络的卷积和池化运算。如图5(a)所示,卷积核初选如图5(b)所示,其中,卷积核类似于传统神经网络中的权值一样,在卷积神经网络训练过程中不断被优化;如果采用ReLU函数作为卷积层的作用函数,则经过一维卷积运算输出的特征图如图5(c)所示。

Figure 5. One dimensional Convolutional operation
图5. 一维卷积运算
根据图5(c)卷积后输出的特征图,作为池化层的输入,如图6(a)所示,然后进行池化运算,即对于2 × 1的区域进行池化操作,得到的池化层输出如图6(b)所示。经过池化运算后的输出作为全连接层的输入,乘以池化层与全连接层的权值求和,再经过作用函数运算得到全连接层的输出。同样,池化层与全连接层的权值也是在卷积神经网络训练过程中不断被优化。最后,全连接层与输出层之间进行权值连接,输出层的输出就是所要估计的力学模型的参数。
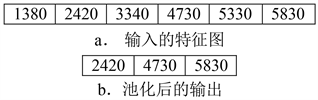
Figure 6. One dimensional maximum pooling operation
图6. 一维最大池化运算
基于卷积神经网络估计力学模型参数的主要步骤如下:
1) 选定卷积神经网络的拓扑结构,确定卷积层、池化层的层数;选定核函数和池化方法;选取神经元的作用函数;
2) 选取神经网络学习的优化算法和目标函数,例如随机梯度搜索算法;确定神经网络中的超参数、收敛准则和最大迭代次数;
3) 基于解析或者数值模型,建立神经网络训练样本集和测试集;
4) 输入神经网络训练样本集,训练神经网络。卷积神经网络常常采用BP框架的随机梯度下降(stochastic Gradient descent)方法,完成神经网络的训练 [19]。
5) 输入神经网络测试集,测试神经网络;
6) 室内进行土体三轴压缩实验,记录不同围压条件下的应力–应变曲线。
7) 将实验数据输入神经网络,估计力学模型参数。将基于神经网络反演得到力学模型参数,代入到已知的力学模型,预测岩土材料的变形曲线,验证方法的有效性。
为了提高深度神经网络的性能,前人提出了一些针对神经网络固有缺陷的算法和方法,总结如下:
1) 学习率衰减方法。如果学习率过大,神经网络训练时,可能不收敛;相反,如果学习率过小,会使得神经网络的收敛速度变慢。该方法随着神经网络学习的进行(迭代),学习率逐渐减小。该方法中典型的代表是AdaGrad算法,此算法会在学习过程中自适应调整学习率,并且使得权值增量较大的,学习率变小。
2) 目标函数的正则化方法 [5] [14],该方法受Tikhonov正则化算法的启发,它也类似于罚函数方法,在均方误差(mean squared error)后面增加了一项
(13)
式中W为神经网络的权值矩阵,
为正则化因子,它也是一个超参数,该参数越大,权重的惩罚就越大。
3) 神经网络训练目标函数除了均方误差之外,还有交叉熵误差作为目标函数 [6],该方法可以提高基于梯度下降法搜索最优网络权值的收敛速度。
(14)
4) 神经网络超参数优化方法。超参数,例如学习率(learning rate),动量项(momentum),隐含层神经元的个数。超参数往往需要进行多次尝试,以便找到一组合理的超参数 [7]。神经网络超参数(hyper parameter)优化问题,与其说是一门科学方法,倒不如说是一门艺术。为了获得比较合理的一组超参数,往往采用试错的方法,经过多次试凑得到。将数据集分为训练数据、验证数据和测试数据。其中,训练数据用于神经网络学习,确定神经网络的权值和阈值,而验证数据用于评估神经网络的超参数,而测试数据用于检验神经网络的泛化能力。超参数的优化问题,可以采用贝叶斯优化方法(Bayesian optimization) [7]。这可能是目前限制神经网络更广泛应用的一个瓶颈。
5) 神经网络初始权值选取的问题。较差的初始权值可能会导致神经网络学习失败。同时,为了防止神经网络初始权值均一化,初始权值应该随机产生。Xavier提出了使用标准差为1/N1/2的高斯分布进行权值初始化的方法,N表示神经元的个数。
6) 抑制过拟合、提高泛化能力的问题。为了解决该问题,Srivastava提出了随机删除神经网络单元方法(Dropout方法) [20]。在神经网络训练过程中,随机选择隐含层的神经元,将其删除(杀死),使其不再传递信号。但是,随机删除某些神经单元方法,删除多少个,删除原则,缺少理论依据。
7) 深度学习输入数据的预处理方法,包括归一化方法、均值减法、均一化方法、白化方法等 [5] [21]。
4. 结论
深度学习是一种机器学习方法,能够根据输入数据的特征,进行分类和递归学习。神经网络从已知的数据中获得规律或者模型,然后根据学习获得的知识对其他数据进行预测分析。深度学习起源于图像识别领域,经过对其改进和补充,能够应用到岩土材料力学模型参数估计中。随着神经网络研究的不断深入,已经开发了许多深度学习研发平台,例如:基于MATLAM的卷积神经网络开发平台 [22] [23],基于Theano的深度学习平台,基于Pylearn2的卷积神经网络平台,基于TensorFLOW的深度学习框架训练卷积神经网络。尽管深度学习神经网络取得了突破性进展,仍然还存在许多需要改进和完善的方面。由于岩土力学模型参数估计实验获得的是多条一维序列,而不是二维图像,因此,需要应用一维卷积神经网络进行力学模型参数估计研究;尽管一维卷积神经网络与二维卷积神经网络在本质上是相同的。
基金项目
国家重点基础研究发展计划“973”项目(2015CB057804);国家自然科学基金资助项目(11572079)。