迭代精化下求解三对角Toeplitz线性方程组的快速算法

A Fast Algorithm for Solving Tridiagonal Toeplitz Linear Systems with Iterative Refinement

摘要: 本文主要讨论如何对三对角Toeplitz线性方程组 进行高精度数值求解。由于系数矩阵A这种比较特殊的结构，使得我们可以设计出快速求解 的直接算法。我们将该算法应用到实际例子的计算过程中，发现大部分例子计算效果显著，但部分例子的计算精度还不能达到计算机机器精度。针对这类达不到计算机机器精度的例子，本文将在快速求解三对角Toeplitz线性方程组 的直接算法基础上，进一步进行迭代精化，从而提高这类例子的计算精度。数值实验表明通过迭代精化，我们算法计算精度可以达到计算机机器精度。

Abstract: This paper mainly discusses how to numerically solve tridiagonal Toeplitz linear systems   efficiently. Since the coefficient matrix A has a special structure, we can design a direct algorithm to quickly solve  . We will apply the above algorithm to the calculation of practical examples and find that the calculation precision of some examples is not as high as that of computer's ma-chine accuracy. In order to improve the precision of algorithm, this paper further carries out iter-ative refinement to quickly solve the tridiagonal Toeplitz linear equations of  . Numerical experiments show that the computational accuracy of our algorithm can reach computer's machine accuracy by iterative refinement.

1. 引言

本文考虑迭代精化下求解三对角Toeplitz线性方程组

$Ax=b,$ (1.1)

$A=\left[\begin{array}{cccc}\alpha & \gamma & & \\ \beta & \ddots & \ddots & \\ & \ddots & \ddots & \gamma \\ & & \beta & \alpha \end{array}\right]$

其中 $A=\text{Tritoep}\left(\beta \mathrm{,}\alpha \mathrm{,}\gamma \right)$ 为三对角Toeplitz矩阵。

关于三对角Toeplitz线性方程组的求解方法主要分为两类：一类是直接法如高斯消元法、循环约简法和特殊LU分解法 [2] [3] [4] 等等。另一类就是迭代法如古典迭代法(Smith迭代法，ADI迭代法 [5] [6] [7] [8] 等)和投影迭代法(Krylov子空间法等)。在不考虑舍入误差的情况下，对于小型稀疏求解线性方程组的问题，我们通常使用直接法求解。因为直接法可以通过改善置换策略，引入尽量少的填充，充分利用硬件的性能设计算法。但当遇到大型稀疏求解线性方程组的问题时，直接解法计算量太大且数值不稳定，而迭代解法数值稳定且易于并行计算，所以这时我们通常使用迭代法求解。

Toeplitz矩阵是一类特殊结构的矩阵，它在数学、科学计算和工程中有着广泛的应用，如信号处理中的图像恢复存储问题、代数微分方程、时间序列和控制理论等。本文主要讨论如何对三对角Toeplitz线性方程组 $Ax=b$ 进行高精度数值求解。由于系数矩阵A这种比较特殊的结构，我们在前面一篇论文中已经设计出快速求解 $Ax=b$ 的直接算法。其系数矩阵主要是上次对角占优、下次对角占优、若对角占优。具体情况如下：

我们首先从系数矩阵为次对角占优情况开始考虑。

$C=\left[\begin{array}{ccccc}0& 1& & & \\ & 0& 1& & \\ & & \ddots & \ddots & \\ & & & 0& 1\\ 1& & & & 0\end{array}\right]$

我们容易得到 $\hat{A}=CA$ 并且具有如下 $2\times 2$ 的块结构

$\begin{array}{l}\hat{A}=\left[\begin{array}{ccccc}\beta & \alpha & \gamma & & \\ & \beta & \alpha & \ddots & \\ & & \ddots & \ddots & \gamma \\ & & & \beta & \alpha \\ \alpha & \gamma & & & 0\end{array}\right]\equiv \left[\begin{array}{cc}{A}_{11}& p\\ w^{\text{T}}& 0\end{array}\right]\mathrm{.}\hfill \end{array}$ (1.2)

我们对 $\hat{A}$ 作如下的 $2\times 2$ 的块LU分解

$\hat{A}=\left[\begin{array}{cc}I& \\ w^{\text{T}}{A}_{11}^{-1}& 1\end{array}\right]\left[\begin{array}{cc}{A}_{11}& p\\ & -w^{\text{T}}{A}_{11}^{-1}p\end{array}\right]\mathrm{.}$ (1.3)

$-w^{\text{T}}{A}_{11}^{-1}p$ 是叫做 $\hat{A}$ 的Schur补。

同样地，要求问题(1.1)的解也就变成了求如下线性方程组的解

$\hat{A}x=\hat{b}$ (1.4)

其中 $\hat{b}=Cb={\left(b_2\mathrm{,}{b}_3\mathrm{,}\cdots \mathrm{,}{b}_n\mathrm{,}{b}_1\right)}^{\text{T}}$。对x和 $\hat{b}$ 做如下格式的划分

$x=\left[\begin{array}{c}{x}_1\\ x_n\end{array}\right],\hat{b}=\left[\begin{array}{c}{b}_2\\ b_1\end{array}\right]\mathrm{.}$

用块LU分解法分解(1.3)，我们就可以通过求下面方程的解来获得方程(1.1)的解

$(\begin{array}{l}{A}_{11}{x}_1+x_{n}p=b_2\mathrm{,}\\ w^{\text{T}}{x}_1=b_1\mathrm{.}\end{array}$ (1.5)

$(\begin{array}{l}{x}_n=\left(w^{\text{T}}v-b_1\right)/w^{\text{T}}u\mathrm{,}\\ x_1=v-x_{n}u\mathrm{.}\end{array}$ (1.6)

为了获得 $x={\left[x_1^{\text{T}}{x}_n\right]}^{\text{T}}$ 的解，我们首先求解如下方程中的 $u$ 和 $v$

$(\begin{array}{l}{A}_{11}u=p\mathrm{,}\\ A_{11}v=b_2\mathrm{.}\end{array}$ (1.7)

通过如下算法，我们得到式(1.7)中方程组的解 $u$ 和 $v$，具体算法如下：

我们注意到，为了得到(1.6)的解 $x_1$ 和 $x_n$，我们需要解(1.7)中的两个线性方程组，其中 $A_{11}$ 是一个上三对角矩阵。显然，向量 $u$ 和 $v$ 可以通过向后代入法求解。此外，由于 $A_{11}$ 是对角占优的，计算出的向量 $u$ 和 $v$ 都是稳定可靠的。

基于以上分析，我们现在可以重新设计求解(1.1)的算法如下

算法2的稳定性取决于第三步的求解 $x_n=\left(w^{\text{T}}v-b_1\right)/w^{\text{T}}u$。如果 $w^{\text{T}}u$ 不是足够小，那么 $x_n$ 的就是相当精确的。因此，我们可以得出结论，我们求解这类线性方程组的算法在数值上是稳定的，计算出的解是可靠的，如果A是下次对角占优的并且 $w^{\text{T}}u$ 不是足够小。

对于计算复杂度，我们的算法需要大约12n (flops)的浮点运算，选主元的LU分解法需要13n (flops)浮点运算，我们的方法与选主元的LU分解法相比需要更少的浮点运算量。对于内存存储空间，我们的算法只需要存储2个大小为n向量，少于选主元的LU分解法需要存储5个大小为n向量。特别是，我们的算法需要较少的数据传输。在数据传输过程中它只需要读取1个向量即右边的向量并写入一个向量(即方程的解)。但是选主元的LU分解法需要读取个向量。正如我们所知，现代计算机有多层的内存结构，有不同的存储级别，如较小的高速缓存和较大的低速磁盘存储。在计算过程中，数据在不同级别的高速缓存中传输。因此，较少数据传输的算法可能会显示出更好的计算性能。这使得该算法比选主元的LU分解方法更有效。

现在，我们考虑上次对角占优的情况。设J为交换对角矩阵，在交叉对角上为1 (从左下到右上)，其他地方为0，即

$J=\left[\begin{array}{ccccc}0& 0& \cdots & 0& 1\\ 0& 0& \cdots & 1& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 1& \cdots & 0& 0\\ 1& 0& \cdots & 0& 0\end{array}\right]\mathrm{,}$ (1.8)

因为A是上次对角占优的， $\tilde{A}=JAJ=\text{Tritoep}\left(\gamma \mathrm{,}\alpha \mathrm{,}\beta \right)$ 是下次对角占优的。因此，我们可以将原来的线性线性方程组(1.1)转化为以下新的线性方程组

$\tilde{A}\tilde{x}=\tilde{b}$ (1.9)

$\tilde{x}=Jx$， $\tilde{b}=Jb$。因此，结合算法2得到下面的算法3用于求解方程(1.1)。

由于J是一个置换矩阵，因此算法3的稳定性、计算复杂度和内存存储都与算法2相同。

最后，我们讨论了不可约对角占优的情形。已知，在这种情况下，A是一个H矩阵，使用LU分解法不需要选主元。显然，这种情况下LU分解法不会导致任何非零元素的填充，但需要更多的内存存储空间。为了避免这个问题，我们采用以下方法：

如果 $\beta >\gamma$，那么我们选择算法2解方程(1.1)，如果 $\beta <\gamma$，然后调用算法3解解方程(1.1)。我们把以上情况总结，得到综合算法如下：

算法4的计算复杂度和内存存储与算法2或3基本相同。

与选主元LU分解法相比，我们提出的三对角Toeplitz线性方程组快速直接算法(算法4)具有以下优点：不仅需要更少的计算时间和存储空间以及数据传输，而且具有更高的计算精度。我们将该算法应用到实际例子的计算过程中，发现大部分例子计算效果显著，但部分例子的计算精度还不能达到计算机机器精度。为解决这类问题，我们将在快速求解三对角Toeplitz线性方程组 $Ax=b$ 的直接算法基础上进行迭代精化(详情见算法5)，从而减小我们的计算误差，提高解的精度。

2. 迭代精化算法及收敛性分析

求解(1.1)的精化迭代法的迭代格式 [12] 为：

$x^{\left(k+1\right)}=x^{\left(k\right)}+d^{\left(k\right)}$ (2.1)

$A{d}^{\left(k\right)}=r^{\left(k\right)},r^{\left(k\right)}=b-A{x}^{\left(k\right)}$ (2.2)

其中 $x^{\left(0\right)}$ 为初始迭代向量， $k=\mathrm{0,1,}\cdots$。当 $d^{\left(k\right)}$ 为(2.2)的精确解时，迭代格式(2.1)~(2.2)退化为单步迭代精化。不难看出，该迭代格式可以提高解 $x^{\left(k\right)}$ 的精度。另外，如果我们用高精度方法求解(2.2)，那么我们把迭代格式(2.1)~(2.2)称为迭代精化。

引理2.1 [12] 假设不考虑舍入误差，精确计算残差 $r^{\left(k\right)}$， $d^{\left(k\right)}$ 为(2.2)的精确解，则 $x^{\left(k+1\right)}$ 为(1.1)的精确解 [9]。

证明：由(2.2)式知 $A{d}^{\left(k\right)}=r^{\left(k\right)}$， $r^{\left(k\right)}=b-A{x}^{\left(k\right)}$，从而 $A{x}^{\left(k+1\right)}=A{x}^{\left(k\right)}+A{d}^{\left(k\right)}=b$。这意味着 $x^{\left(k+1\right)}$ 是(1.1)的精确解，证毕。

结合引理2.1与算法4，我们得到迭代精化 [10] 的具体算法如下：

定理2.1 [12] 假设r是双精度并且 $\kappa \left(A\right)\cdot \epsilon <c\equiv \frac{1}{3n^{3}g+1}<1$，n表示矩阵A的阶数，g表示主元增长

因子， $\kappa \left(A\right)=\Vert A\Vert \cdot \Vert A^{-1}\Vert$。那么迭代精化收敛于：

$\frac{\Vert x^i-A^{-1}b\Vert }{\Vert A^{-1}b\Vert }=o\left(\epsilon \right)\mathrm{.}$ (2.3)

定理2.2 [12] 令 $x^{\mathrm{<mo>\; *\; </mo>}}$ 为线性方程组(1.1)的精确解。对第k步迭代，用算法5求解(2.2)的初始迭代向量均为 $d^{\left(0\right)}=x^{\left(0\right)}$ (其中 $x^{\left(0\right)}$ 为用算法4求得的线性方程组(1.1)的解)，相应的迭代序列为 $d^{\left(k\right)}$，且 $d^{\left(k\right)}$ 满足终止检验公式

$\eta =\frac{\Vert r^{\left(k\right)}-A{d}^{\left(k\right)}\Vert }{\Vert r^{\left(k\right)}\Vert }<\epsilon$ (2.4)

则迭代序列 $x^{\left(k\right)}$ 满足

$\Vert x^{\left(k+1\right)}-x^{\mathrm{<mo>\; *\; </mo>}}\Vert \le \kappa \left(A\right)\epsilon \Vert x^{\left(k\right)}-x^{\mathrm{<mo>\; *\; </mo>}}\Vert$ (2.5)

特别地，当 $\kappa \left(A\right)\epsilon <1$，迭代序列 $x^{\left(k\right)}$ 收敛到 $x^{(\ast )}$ [11]。

证明：由(2.1)、(2.2)及(2.4)式知

(2.6)

从而

(2.7)

当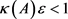时，迭代序列收敛，证毕。

针对算法5，只要，则满足终止检验公式(2.4)，那么就是满足计算机机器精度的解 [12]。

3. 数值实验

下面我们用一些例子证明我们算法的有效性。本文所有数值实验的电脑运行环境为：Intel(R) Core(TM) i3-2310M CPU @2.10 by Matlab 7.4.0.287 (R2014a)。分别用快速直接算法和加迭代精化的快速直接法分别对三对角Toeplitz线性方程组进行求解。选取典型代表例子如下：

例1：；

例2：。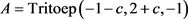

在例1、例2中的矩阵A是由一维对流扩散方程离散差分得到的方程的系数矩阵。在所有例子中二阶差分都采用中心差分格式。但在例1和例2中一阶差分分别使用中心差分格式和向后差分格式。在数值实验中，我们计算了许多不同n和参数c的例子。我们可以得到共同的结论。接下来我们展示一些有代表性的例子结果。在实验中，n表示矩阵A的阶数，Iter表示迭代次数，CPU表示计算时间，右端向量

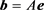，R表示计算相对残差，即()，Fast algorithm表示快速算法，Iter algorithm表示对快

速算法进行迭代精化。

数值结果表1是例1取和的两个例子，数值结果表2是例2取和的两个例子。我们发现当我们用直接算法1计算三对角Toeplitz线性方程组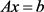时，存在计算精度无法达到机器精度的情况。但是通过我们进一步迭代精化，当迭代一定次数(本例Iter = 10)时，我们的计算精度就可以达到计算机机器精度。

Table 1.

表1.

Table 2.

表2.

数值实验表明，当采用直接算法求解三对角Toeplitz线性方程组的时候，存在计算精度达不到计算机机器精度的情况。但是通过我们的迭代精化算法，可以使三对角Toeplitz线性方程组的解都能够达到计算机机器精度。

基金项目

2019年硕士研究生校级科研创新项目(CX2019SS34)。