1. 引言
四旋翼编队在环境勘测、任务侦查等实际应用中的巨大潜力 [1],编队作业相较于单架次在高效性、鲁棒性和覆盖能力等方面更具有优越性 [2],近年来,涌现出大量四旋翼编队的协同控制研究成果,如行为控制法 [3]、领航跟随法 [4] 和基于虚拟结构 [5] 的编队方法。四旋翼编队之间一般采用集中式控制 [6],分散式控制 [7] 和分布式控制 [8] 进行信息交互。在分布式编队控制中,由于四旋翼编队间相互作用的拓扑结构,各四旋翼只能获取部分的相对信息,这需要控制方式容错率和扩展性都非常强。
圆形编队是编队控制中的常见队形之一。近年来,其算法引起了国内外众多学者的关注 [9]。随着半同步模型的发展 [10],大量的研究成果 [11] 为分布式控制圆形编队奠定了基础。Flocchini [12] 提出了在圆形上部署均匀分布的编队控制方法。王晨 [13] 考虑了在圆形上形成期望的相对位置分布,利用变增益技术给出了在有限时间内的编队控制。文 [14] 进一步考虑了受约束的机器人运动,提出了时变、离散的闭环控制。然而,这些研究结果始终限制在圆的一维空间中移动。
对于二维平面中的圆形编队控制,X Défago和A Konagaya [11] 提出将圆形编队问题分解成收敛和均匀分布两个子问题并分别求解的解耦控制算法。在此基础上,文 [15] 提出了一种基于极限环的解耦设计方法,能够将平面上的圆形编队问题解耦为目标盘旋和间距调整,并分别设计了汇聚和布局组成的分布式控制器。
然而,该控制器控制平面上的一组多机器人渐近地形成圆形编队的过程需要耗费较多时间。如何加快圆形分布的速度,使其能够在有限时间内完成,文 [16] 将Lyapunov函数的规律性与整定时间联系起来,设计了一种用于系统有限时间编队控制律,为本文四旋翼空间圆形编队控制器的设计提供了改进思路。本文还充分考虑四旋翼在空间中占据体积,设计避碰控制器,保证多四旋翼在形成编队的过程中不会相互碰撞。
本文的内容安排如下。第二节对空间四旋翼系统进行建模,分别介绍了四旋翼数学模型、系统感知拓扑结构及队形。第三节进行四旋翼空间圆形编队控制器设计。第四节对所设计的控制器进行数值仿真和实验验证,最终证明了所设计空间圆形编队控制器的有效性、有限时间形成圆形分布和避免碰撞的特性。
2. 四旋翼建模
在主要的控制器设计和算法给出之前,有必要分析一下四旋翼编队模型。首先,引出四旋翼的数学模型,介绍其参数含义、动态模型以及坐标变换关系;然后,将描述四旋翼系统的感知拓扑结构以及编队队形。
2.1. 四旋翼数学模型

Figure 1. Schematic diagram of type X quadrotor
图1. X型四旋翼示意图
本文的实验采用的是基于Pixhawk飞控、轴距为240 mm的X型四旋翼,其外形和螺旋桨转向如图1所示。分别记机体坐标系上的
轴、
轴和
轴方向上的转矩为
、
和
,其表达式如式1。四旋翼的空间位置信息在四旋翼大地坐标系
中采集,
为四旋翼在大地坐标系下的位置,而姿态角和受力情况则在机体坐标系
中测量,
为四旋翼大地坐标系下的位置,本实验采用的四旋翼主要参数见表1。

Table 1. Parameters and their description
表1. 参数及其含义
(1)
其中,
为第i号电机的转速。
一般地,不计空气阻力,记
为四个螺旋桨总拉力,四个旋翼的转速代数和为
,可得如下动态模型 [17] 如式2:
(2)
其中
、
、
为四旋翼的横滚角、俯仰角和偏航角。
由于本文是在具有一定高度的水平面上对四旋翼进行位置控制,当圆形编队位置控制器计算出位置目标加速度
和
后,需要进行姿态反解,计算出机体的目标姿态欧拉角
和
,进而控制四旋翼系统在水平面内运动。
由式3将大地坐标系下的加速度
和
的转换为机体坐标系下的加速度
和
。
(3)
由式2、式3可求解机体坐标系下的目标欧拉角
和
如式4:
(4)
随后,将通过控制各四旋翼的姿态角度
和
,得到四旋翼的稳定姿态控制,进而得到四旋翼在大地坐标系下的空间圆形编队位置控制。
2.2. 系统感知拓扑结构及队形
有了以上的四旋翼数学模型,下面将介绍四旋翼系统的感知拓扑结构以及编队队形的描述。
本文考虑四旋翼的实际体积,各四旋翼与相邻四旋翼在空间中需要避免碰撞,如图2所示的投影平面上有两个四旋翼a和b,定义相邻四旋翼之间的最小安全距离为
,即四旋翼a和b避免碰撞的极限情况距离,需要满足中心距离
。接着定义避免碰撞距离为
,即当
时,需要进行避免碰撞措施。

Figure 2. (a) Minimum safety distance; (b) Collision avoidance distance
图2. (a) 最小安全距离;(b) 避免碰撞距离
本文考虑一组由N个四旋翼组成的系统,每个四旋翼可由编号i表示,其中
,四旋翼i的位置
,圆形编队的圆心位置
,则各四旋翼关于目标圆心的相对位置
可分别用直角坐标系和柱坐标系方式表示为式5和式6:
(5)
(6)
其中,在四旋翼空间系统的垂直投影水平面上,
为四旋翼i中心相对于目标中心的距离,
为各四旋翼对于目标点的方位角。

Figure 3. Top view of the quadrotor space system number
图3. 四旋翼空间系统编号的俯视图
各四旋翼由相对目标圆心的方位角
的递增顺序决定编号顺序,而对于同一方位角,则编号按与目标点的距离递增排序,如图3所示。由此可以得到与四旋翼i相邻的四旋翼编号为式7:
和
(7)
本文考虑每个四旋翼只能获得相对目标圆心和相邻编号的四旋翼水平位置信息,可将四旋翼系统感知拓扑描述为
,其中
表示四旋翼集合,而
表示相邻关系集合。各四旋翼自身可感知的拓扑结构信息如式8和图4所示。
(8)
其中,在四旋翼空间垂直投影水平面上,
为四旋翼i中心到四旋翼
中心的相对距离。并且定义
为从四旋翼i到
的角距离,为目标圆心延伸到四旋翼i的直线经过逆时针旋转至四旋翼
而形成的角度;同理可以获得四旋翼
到四旋翼i的相对距离
和角距离
。
接着,本文考虑期望的四旋翼空间圆形编队的队形由高度h、半径r和圆形相对位置分布d描述。设
代表从i到
的期望水平角距离,而每个四旋翼i只利用信息
和
,那么可由下式9表示期望的圆形相对位置分布。
(9)

Figure 4. Top view of topological structure information perceptible by each quadrotor
图4. 各四旋翼自身可感知的拓扑结构信息俯视图
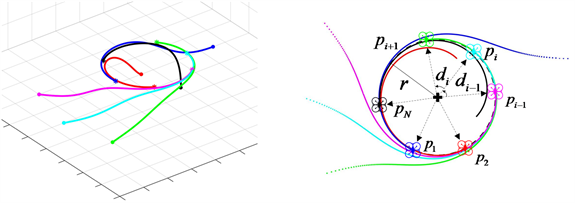
Figure 5. (a) Space formation trajectory; (b) Top view of quadrotor space trajectory and expected formation description
图5. (a) 空间编队轨迹;(b) 四旋翼空间轨迹及期望队形描述俯视图
最后,该空间圆形编队形成过程可由图5的轨迹表示:四旋翼由初始位置起飞,控制飞至设定高度,同时盘旋着向圆形收敛,并调整圆上四旋翼的相对位置分布,最终形成期望的队形并不断盘旋。
因此,本文的思路是将其空间圆形编队控制器建模为如下单积分模型式10:
(10)
其中
为将被设计的控制输入,即
轴方向的期望速度。为了便于下文叙述论证,提出如下关于空间圆形编队问题的定义。
定义(空间圆形编队问题):给定一个在空间上用高度h、半径r和图形分布d描述的空间圆形编队,设计分布式控制律
,在各四旋翼按空间分布逆时针排序的条件下,式10的解将趋于平衡点
,将满足下式11:
(11)
由定义,空间圆形编队问题被转换成仅使用四旋翼与目标之间的相对位置与相邻四旋翼之间的相对位置来设计所有四旋翼的自身控制器,使得所有四旋翼控制在设定高度,形成设定半径的圆形分布,同时在有限时间内形成期望的圆形相对位置分布,能够保证四旋翼之间的避免碰撞,形成围绕目标旋转的编队队形。
3. 控制器设计

Figure 6. Block diagram of the quadrotors space circular formation controller
图6. 四旋翼空间圆形编队控制器控制结构图
在本节中,四旋翼空间圆形编队问题的控制器控制结构图如图6所示。空间圆形编队问题被解耦为垂直方向的高度控制和水平方向的圆形编队控制问题,其中各四旋翼在水平面上的运动可由四旋翼通过俯仰和横滚运动完成。将三维圆形编队位置控制器解析来看,高度控制能够使四旋翼控制在设定的飞行高度、圆形汇聚控制使各四旋翼进行水平方向的圆形汇聚盘旋、间距布局控制使各四旋翼的个体进行间距调整,使其能在有限时间内形成设定的圆形相对位置分布。同时,还需要考虑四旋翼的实际大小,进行避免碰撞控制。
3.1. 高度控制
本节考虑四旋翼系统需要在期望高度的水平面上进行编队飞行,由于四旋翼的高度控制与水平面控制解耦合,故可采用基于偏差控制的PID控制律,则设计的控制器高度控制如下式12:
(12)
其中,
分别为比例系数、积分时间常数和微分时间常数,
为各四旋翼实际的高度与期望的高度偏差。该高度控制控制器能够控制四旋翼在设定的空间圆形编队高度上飞行。
3.2. 圆形汇聚控制
在汇聚圆形的控制上利用具有稳定极限环的振荡器,其特性为极限周期附近的轨迹将随着时间的推移最终趋于极限环,能够很好地满足本文所要设计的圆形汇聚的要求。由此,将采用一个二阶非线性振荡器,并且该极限环以目标点为圆心,具有期望的圆形半径。设计的极限环振荡器作为圆形汇聚控制
如下式13:
(13)
其中
,
为常数,
。需要注意的是,圆形汇聚控制
仅使用四旋翼i和目标圆心之间的相对位置信息,用于处理圆形收敛盘旋问题,即每个四旋翼围绕目标
以半径r逆时针旋转。
3.3. 间距布局控制
为了形成期望的圆形分布,四旋翼i还需要和相邻的四旋翼利用相对位置信息来协调控制。因此在设计控制器的分布控制时,个体间距调整需要聚焦于四旋翼两两之间的角距离
,设计的圆形相对位置分布控制律如下式14:
(14)
其中,
为且
,
,可在有限时间内形成四旋翼圆形相对位置分布;当
时,形成四旋翼圆形相对位置分布的过程是渐近的。接着,设计的间距布局控制器
为下式15:
(15)
其中,
为常数,
。该间距布局控制器可用于处理个体间距调整这一目标,即多四旋翼需要形成期望的圆形相对位置分布d。
3.4. 避免碰撞控制
本节考虑四旋翼的实际大小,考虑各四旋翼与相邻四旋翼在空间中的外形垂直圆柱体之间需要避免碰撞。故采用人工势场法来保证避免碰撞,当相邻四旋翼之间的水平距离小于一定距离时,势场作用力便使相邻四旋翼向相反的方向移动。考虑文 [18] 中采用的方法,定义相邻四旋翼之间的势场函数如下式16:
(16)
其中,
,如第二节介绍,
表示避碰距离,
表示最小安全距离,当两个四旋翼的距离处于最小安全距离和避碰距离之中时,
才为非零值。对于整个多四旋翼系统拓扑结构而言,保证每个四旋翼和相邻四旋翼之间的避免碰撞,就可以保证整个多四旋翼系统避免碰撞,从而上述的
中的j只需要考虑的是
和
。然后
对
求偏导,得到下式17:
(17)
接着定义函数
如下式18:
(18)
其中,
的值越大,说明第i个四旋翼与相邻四旋翼的一个或两个间的距离越接近最小安全距离,因此采用梯度下降法来使得
取得最小值便可保证避免碰撞。本文将避免碰撞控制器设计如下19:
(19)
其中,
,避免碰撞控制器的控制输入为
轴的速度信号。
3.5. 空间圆形编队控制器融合
如前文所述,四旋翼空间圆形编队问题包括机组高度控制、圆形收敛盘旋和个体间距调整三个子问题,由文 [15] 中解耦设计的思想,本文设计一个由高度控制
、圆形汇聚控制
和间距布局控制
组成的分布式控制器,再结合避免碰撞控制器
,形成空间圆形编队整体控制器如下式20:
(20)
其中
为避碰控制器的系数,用于调节避免碰撞的灵敏度。
为使
与间距布局控制结合仍适用于圆形编队控制器,文 [15] 已讨论和证明需要限制
为正且有界的条件,而本文的间距布局控制可满足该条件。
式20中,所求的控制量
即四旋翼相对于目标圆心的目标速度,而水平面上的运动控制量还需按下式21转换为大地坐标系下的目标加速度。
(21)
其中
再带入式4进行姿态解算,进而得到设定的欧拉角。
4. 仿真与实验
前文已详细阐述了四旋翼的运动学模型以及空间圆形编队控制器的控制原理,接下来将在MATLAB中进行仿真实验,以及在VICON系统作为大地坐标系下的位置传感器环境中实现3个四旋翼的空间圆形编队控制。
由前2.2节空间圆形编队问题的定义中,设定以下参数为如表2所示:

Table 2. Space circular formation parameters
表2. 空间圆形编队参数
为了体现四旋翼空间圆形编队控制器的有效性、避免碰撞控制器的效果以及圆形相对位置分布有限时间内形成的效果,进行下列实验。
4.1. 仿真结果
本文四旋翼空间圆形编队控制器可以通过参数
调整,其中,
可以改变圆形收敛速度,而
可以改变旋转速度。通过多次调参,选取参数
,
,
,
,
,
,
,设置无避免碰撞和圆形相对位置分布渐近形成的圆形编队控制器参数为
,仿真效果图如图7,可以发现各四旋翼相对距离曾低于
。保持参数
大小不变,在
和
之间进行避免碰撞控制,设置圆形编队控制器参数为
,如图8所示,可以发现各四旋翼相对距离不曾低于
。进一步对避免碰撞和圆形相对位置分布有限时间内形成的圆形编队控制器参数为
,如图9所示,可以发现有限时间内形成期望的圆形分布。

Figure 7. For parameter
, the simulation diagram is formed by the asymptotic distribution of circular relative positions without avoiding collision
图7. 参数
时无避免碰撞、圆形相对位置分布渐近形成仿真图

Figure 8. For parameter
, the simulation diagram is formed by the asymptotic distribution of circular relative positions and avoiding collision
图8. 参数
时避免碰撞、圆形相对位置分布渐近形成仿真图

Figure 9. For parameter
, the simulation diagram is formed by circular relative positions and avoiding collision in limited time
图9. 参数
时避免碰撞、圆形相对位置分布有限时间内形成仿真图
4.2. 实验验证
接下来进行实物验证,各四旋翼由初始位置上升至设定高度,同时进行水平方向的圆形编队盘旋,实际飞行的效果如图10所示。选取上述有避免碰撞、圆形相对位置分布渐近形成和圆形相对位置分布有限时间内形成的两组仿真实验参数,进行飞行实验,得到实际飞行数据记录图如图11和图12所示。
如实际飞行轨迹图11和图12所示,与仿真轨迹有着较高的拟合度,故可验证该四旋翼空间圆形编队控制器的有效性,同时可以看出避免碰撞控制器的特性,以及本文改进的圆形相对位置分布有限时间内形成的效果。

Figure 11. The actual flight data record graph formed by the asymptotic distribution of circular relative position
图11. 圆形相对位置分布渐近形成的实际飞行数据记录图

Figure 12. The actual flight data record graph formed in a finite time by the circular relative position distribution
图12. 圆形相对位置分布有限时间内形成的实际飞行数据记录图
5. 总结与展望
本文研究了四旋翼空间圆形编队问题,考虑了各四旋翼之间的避免碰撞,控制四旋翼在一定高度进行圆形收敛,围绕圆心在圆形上旋转,并在有限时间内形成期望的圆形相对位置分布。设计了基于极限环的解耦设计方法,利用四旋翼与目标圆心以及相邻四旋翼的位置信息,设计一个高度控制、圆形汇聚控制和间距布局控制组成的分布式控制器,其中高度控制用PID控制四旋翼组维持在一定高度,圆形汇聚用极限环振荡器驱动四旋翼进行圆形收敛并旋转,而间距布局利用避免碰撞条件,控制四旋翼之间的角距离,在有限时间内形成期望的空间圆形编队。最后,给出了仿真和实验,验证了空间圆形编队有限时间控制器的有效性。
基金项目
国家自然科学基金面上项目(No. 61973164)资助。
NOTES
*通讯作者。