1. 引言
Toeplitz算子的有限乘积有限和问题在算子理论研究中具备着重要的代数意义,算子的乘积问题,是算子理论探究中的热点问题,由于其复杂多变性,通过查阅资料发现,国内许多学者对算子的有限乘积有限和问题的研究有很大兴趣。在文献 [1] 中证明了下面刻画了两个以有界调和函数为符号的一类算子
,
,并探究了这类算子的有限乘积相加之和
为零算子和紧算子的等价条件。将上述问题推广到
调和Bergman空间上的情况相对复杂,Yufeng Lu,Qian Ding等人 [2] 在2017年经过计算与推广发现,得到关于两类特殊符号的Toeplitz算子乘积的有限秩的结论。而对于Bergman空间上的有限乘积有限和问题,将其推广到某类特殊符号的Toeplitz算子上还有待探究,因此本文对Bergman空间上某类符号Toeplitz算子的乘积有限和问题进行了推广与计算,进而分析证明得到其为零算子的一个必要条件。
2. 预备知识
在这一部分中,我们介绍了Berezin变换和Mellin变换,并用第二个变换来表示第一个变换,我们将在下一节中使用这个公式。
定义2.1 若
是
上的可积函数,可定义Mellin变换:
.
Mellin变换是半平面
上的有界解析函数。由于三角多项式在
中是稠密的,所以有如下极分解表示
,
其中
,因此对任
,有
,则f的极分解
为
Mellin变换是由其零点所唯一确定,并有以下结论。
引理2.1 [3] 若
为
上的有界解析函数,在两两不相同的点列
上取值为零,若
1)
,
2)
,
则
在半平面
上恒等于零。
注解:我们经常用到引理2.1的一种特殊情况:若
为
上的有界解析函数,若存在自然数序列
使得
且
,
则
。
定义2.2 Mellin卷积的定义,可用
表示f和g的Mellin卷积:
.
其中乘法
是通过上述变量的变化与正规卷积有关的。很容易看出Mellin变换将卷积转化为点积,即:
,
如果f和g在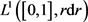 中,则
也是。
中,则
也是。
定义2.3 若
,f的Berezin变换记为Bf:
,
.
本文要用到Berezin变换的极坐标表示,Čučković Ž给出下述定理。
引理2.2 [4] 若
,对
,则f的Berezin变换Bf有如下的极坐标表达式:
下面我们来描述
上关于Berezin变换的不动点问题,这比在
上的不动点问题困难的多。回顾复平面上的Laplacian (拉普拉斯)变换为:
.
在处理Berezin变换时,使用如下的不变拉普拉斯变换将更为方便:
,
其中f是D上的任意一个二次可微函数。
引理2.3 若f在D上是二次可微的,则
, 对任意
.
其中
表示D的全纯自同构群,任给
,存在唯一
满足:
是对合的,即
为恒等映射,并且
,
。
定义2.4 一个解析函数
,如果满足
.
则称为函数f为Bloch函数。
为了避免下文中的重复,我们认为如果函数的极分解只有负幂项,则称它具有性质(N)。
3. 主要结果
定理3.1 假设
,
,
;
且
。若
,则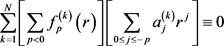 。
。
证明:对
,
.
进而,
.
由
,得
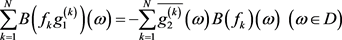 .
.
由引理2.2,令
,得
,
而
的极分解式中关于
的负幂项系数为0,故系数函数对应的Mellin变换为0,进而关于
的系数为0,即
,
进而
具有性质(N) (
)。
另一方面,记
,
综上,
具有性质(N),因而
具有性质(N)。由
,则
具有性质(N),往证
具有性质(N)。
令
,由引理2.3,
在
范数下收敛到
,对
两边求不变Laplacian变换
得,
.
计算可得,
.
由
解析,故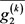 具有性质(N);
具有性质(N);
又
因为
具有性质(N)。故
极分解表达式中有
(
)。
所以
具有性质(N)。
进一步,
具有性质(N)。其极分解为关于
的表达式。综合以上计算结果,
具有性质(N)。且极分解表达式的首项为关于
的单项式。进而
具有性质(N)且首项为关于
的单项式。
下证
。
因为
为Bloch函数,故
有界。因为Berezin变换把
映成
。故
。
另一方面,
故
。
由前面已证结果中的前三项都在
中,而
.
所以
,故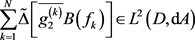 。
。
进一步可知,
且具有性质(N)。进而,在
中,
依范数收敛
,而
的极分解式中,只有
负幂项,进而
具有性质(N)。而
只有负幂项,即当
时,有
上面证明了某一类符号的Toeplitz算子有限乘积有限和为零算子的必要条件。下面我们来思考其逆否命题是否成立。
推论3.2 假设
,其中
,
,
。若
,则
。
例3.1 若
,其中
,则
。
4. 结论
本文讨论Bergman空间上两个形如
,
的Toeplitz算子,其中
,
,
,
。在进行大量的查阅资料和推算
下,探究Toeplitz算子
,
的乘积有限和的相关问题,得到以下结论:
1) 假设
,若
,则
。
2) 假设
,若
,则
。
参考文献