1. 引言
在许多实际问题中,需要利用系统过去时刻的状态,因而提出了延迟微分方程模型。延迟微分方程也称时滞微分方程,属于泛函微分方程。它们在图形处理、计算机科学、生态、经济、物理、人口动力学、生物医学等各个科学领域有着广泛的应用。正因为延迟微分方程具有很强的应用背景,它们的研究受到了人们的长期关注(见文献 [1] - [6] 及其参考文献)。与经典微分方程相比,它们的解不仅与当前的状态有关,还受过去一段时间的影响。延迟项的存在不仅给理论研究带来困难,也给数值研究带来了挑战。近些年来,在延迟抛物方程的数值研究方面,已有不少成果。文献 [2] [3] 研究了非线性延迟抛物方程的紧致差分法及其理论。文献 [4] 研究了变系数时滞反应扩散方程的紧致差分法。文献 [5] 研究了时间分数阶变系数时滞抛物方程的紧致差分法及其收敛性。然而,人们对延迟双曲方程的数值研究关注不多。文献 [6] 研究了一维时滞波动的紧致差分法及其Richardson外推法。
显式差分法虽然是条件稳定的,但是由于不需要解线性方程组,程序易于实现、计算量小等优势受到人们的青睐。特别对二阶波动来说,稳定条件是可接受的,并不苛刻。此外,为了克服抛物方程显式差分法的稳定条件的限制,提出无条件稳定的 Du Fort-Frankel格式。本文推广经典波动方程的显式差分格式,对如下非线性延迟波动方程
,
,
, (1a)
,
,
, (1b)
,
,
, (1c)
建立两类差分格式及其算法理论。
2. 差分格式
2.1. 记号
为了用差分方法求解问题(1a)~(1c),我们对
做剖分。将空间区间
剖分m等份(m为整数),记空间步长
(
)。在时间方向上,采用限制性网格时间步长
(
),
均为整数,记
,
,
,
,
均为整数。在结点
处的精确解和数值解分别记为
,
。记网格剖分区域
,定义网格函数空间
,对任意
,引用差分算子,内积和范数如下
,
,
,
,
,
,
,
,
.
2.2. 两类差分格式的建立
由泰勒展式可知
,
.
从而,在结点
处用差分算子
,
离散
,
可得
,
,
, (2)
其中,
,
,
. (3)
用
代替
,略去小量项
,得到第一个差分格式
,
,
, (4a)
,
,
, (4b)
,
,
. (4c)
记网格步长比
,对差分算子
做如下处理
. (5)
将(5)式代入(2)式中得
,
,
, (6)
其中
,
,
. (7)
舍去(6)式的
项,用
代替
,便得到了第二个差分格式
,
,
, (8a)
,
,
, (8b)
,
,
. (8c)
2.3. 差分格式的收敛性分析
为研究上述两个差分格式的收敛性,我们现引入两个引理。
引理2.1 [7] 设
,则有下列不等式成立
,
,
,
.
引理2.2 [8] 设A和B是非负常数,
是非负序列且满足
, 则
此外,若
,则
。其中
足够小,使得
。
另外,存在常数
,使得
,
,
, (9)
,
,
, (10)
成立。
假设
满足局部Lipschitz条件。设u,v为问题方程(1a)~(1c)的真解,且存在正常数
,
,当
,(
),函数
满足如下等式
(11)
成立,其中
为Lipschitz常数。
定理2.1 设问题(1a)~(1c)在节点
的精确解为
,
为差分格式 (4a)~(4c)的解。记
。当
时且步长满足以下条件
,
,
则有,当
时,下列估计
,
, (12a)
,
, (12b)
成立。此处
。
证明 将方程(2)式与(4a)式相减,得到误差方程
,
,
, (13a)
,
,
, (13b)
,
或
,
. (13c)
当
时,
,显然(12a)式与(12b)式成立。
假设当
时,(12a)式成立,则当步长满足
,
时,应用引理2.1可知
,
.
记
为
,
为
。运用不等式
和(11) 式可得
,
. (14)
记
。当
时,对(13a)式两端同时与
做內积,运用引理2.1得
. (15)
运用等式
和引理2.1,可得
. (16)
由(16)式可得
,
. (17)
由不等式
和不等式
可得
. (18)
. (19)
另外,由
有
,
. (20)
将上式两端平方后,运用均值不等式
得
,
. (21)
在(21)式两端乘以
并对i求和,结合(17)式可得
,
. (22)
将估计项(18)~(19)代入式子(15)后,运用(22)式和引理2.1得
. (23)
将上式中的k用p替换,两端同时乘以
,并对p从−1到k求和可得
. (24)
当
时,在(24)式中运用引理2.2可推得
,
. (25)
在(25)式中令
,运用(22)式和引理2.1,可得
,
.
故当
时假设依然成立。由数学归纳法可知定理成立。
定理2.2 设问题(1a)~(1c)在节点
的精确解为
,原问题格式(8a)~(8c)的数值解为
。记
。当步长满足
,
,
, (26)
时,则在
的条件下,有
,
, (27a)
,
, (27b)
成立,其中
。
证明 将方程(6)式与(8a)式相减,得到误差方程组
,
,
(28a)
,
,
, (28b)
, 或
,
. (28c)
或
,
. (28c)
当
时,
,显然(27a)式与(27b)式成立。
假设当
时,(27a)式成立,则当步长满足(26)时,应用引理2.1可知
,
.
从而,运用(11)式可得
,
.(29)
记
,对(28a)式两端与
做內积,运用离散的格林公式得
. (30)
借用(16)式的处理技巧,不难得到
. (31)
由(31)式可得
,
. (32)
应用不等式
和不等式
可得
(33)
. (34)
运用与(22)式相同的分析方法可得
,
. (35)
将估计项(33)~(35)代入式子(30)中,运用(35)式和引理2.1得
. (36)
将上式中的k用p替换,两端同时乘以
,并对p从0到k求和可得
. (37)
当
时,在(37)式运用引理2.2,我们有
,
. (38)
在(38)式中令
时,应用(34)式有
,
.
从而,当
时假设依然成立。由数学归纳法知定理2.2成立。
3. 数值实验
算例 应用格式(4a)~(4c)和(8a)~(8c)计算如下非线性初边值问题:
,
,
,
,
,
,
,
其中,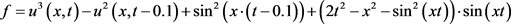 。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,
。
。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,
。

Table 1. FDM (4a)~(4c) maximum error for numerical solution
表1. 差分方法(4a)~(4c)在最大范数意义下数值解的误差

Table 2. FDM (8a)~(8c) maximum error for numerical solution
表2. 差分方法(8a)~(8c)在最大范数意义下数值解的误差
数值结果表明两类显式差分格式在时空方向具有二阶精度。格式(4a)~(4c)的计算效果更好一些。
4. 结论
本文受经典波动方程的显式差分法和抛物方程的Du Fort-Frankel差分法的启发,对非线性延迟波动方程问题建立了两类显式差分法。运用能量法,我们证明了它们在时、空方向上均有二阶收敛性。数值结果验证了理论结果的正确性。
基金项目
国家自然科学基金项目(No. 11861047)。
参考文献