1. 引言
分类问题是监督学习的一个核心问题。在监督学习中,当输出变量 取有限个离散值时,预测问题就变成了分类问题 [1]。任何分类算法的目标都是基于具有类别的给定数据构建模型,然后使用该模型对新实例进行分类。对分类方法的研究主要用于解决实际问题,获得至少比猜测更好的分类精度。例如,在乳腺癌测试中,广泛使用的乳腺癌诊断工具是细针穿刺细胞学检查(Fine Needle Aspiration Cytology: FNAC)。FNAC的正确分类率约为90%,因此迫切需要改进分类系统,协助医生进行诊断来提高乳腺癌诊断的准确率 [2]。
在常规的分类算法中,通常假定属性对类标签具有完全相同的影响,并且在不考虑特征对类的可能存在不同程度影响的情况下构建分类模型。然而,在大多数现实情况下,不同属性对类标签确实存在不同程度的影响。加权分类可以有效地解决此类问题,通过为不同属性赋予相应的权重,以区分其在分类任务中不同的重要程度来获得更好的分类模型。将属性加权方法应用到机器学习模型中的研究越来越受到关注。Zaidi等人在2013年的研究中提出一种加权朴素贝叶斯算法,该算法以最小化均方误差函数为目标,通过赋予分类特征权重来弱化条件独立性假设 [3];Xueson Yan等人在2016年的相关研究中提出了一种双重加权朴素贝叶斯分类器,将属性加权与样本加权共同整合到分类模型中,用于多分类任务 [4]。1977年,Wettschereck和Mohri提出了一种区分懒惰学习算法中权重设置的框架,并通过实验比较分析了各个方法的性能 [5]。Gipta在2012年的研究中提出一种动态加权k近邻分类算法,该算法通过k-Means聚类方法来确定属性权重 [6]。
在本文中,我们提出了一种基于互信息的权重确定方法,并将该方法应用到两种经典的机器学习方法中,提出加权朴素贝叶斯分类器和加权k近邻方法。以解决分类任务中的属性加权问题。我们通过将这些方法的性能与传统方法的性能进行比较来评估本文提出的加权分类方法。通过实验验证本文提出的基于互信息的加权方法的有效性和合理性。
本文的其余部分安排如下。第2部分介绍相关理论知识和方法。第3部分介绍了本文的实验和相应的结果。最后,第4部分对本文提出的方法进行了分析讨论。
2. 方法
2.1. 权重获取
在统计学中,权函数是指在计算平均数等指标时,为各个变量值计算轻重作用的数值的函数。权函数可以被视为执行求和、积分、乘积和平均这些运算的数学系统 [2]。它的主要作用是增强同一数据集中某些变量对结果的影响。在统计分析中,经常会用到权函数的概念,如加权和以及加权平均数。根据取值的不同,权重可以分为离散型和连续型权重,不同的取值类型有不同的定义方式。本文仅讨论离散条件下的权函数。
权函数
定义为离散集X上的取值为正的函数。本文使用的加权和以及加权积分别定义为:
(1)
(2)
对于分类任务,特征加权是提高分类准确性的有效技术,尤其是对于那些不同特征对类别标签有不同程度影响的数据集。由于互信息是两个变量之间相互独立性的度量,互信息越大,说明其中一个变量中所包含的有关另一个变量的信息越多,从而表明两个变量之间的联系越紧密。并且,标准化互信息
的取值范围与权重的取值范围契合,节省了专门进行权重归一化的时间。因此我们将每个特征与类标签之间的标准化互信息作为其权重。假设数据集T的样本量为N,X为数据集中的一个离散型特征,C为类标签变量。其中X、C的取值分别为
和
,则属性X的每个取值的权重
定义如下:
(3)
其中,
(4)
(5)
(6)
2.2. 加权朴素贝叶斯分类器
朴素贝叶斯分类器是贝叶斯决策论(Bayesian decision theory)中的一种基本分类方法。在所有相关概率都已知的理想情况下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记 [7]。在朴素贝叶斯分类器中,由于条件独立性假设的存在,使得所有分类特征对于计算后验概率的贡献相同,然而,在大多数实际应用中,情况并非如此。为了解决这一问题,研究者们提出了一些半朴素贝叶斯分类器,即在分类过程中适当考虑某些属性之间的相互依赖关系,如TAN (Tree Augmented naïve Bayes)以及AODE (Averaged One-Dependent Estimator)。
本文提出加权朴素贝叶斯分类器通过在计算后验概率时对属性加权来完成分类任务,以减少属性条件独立性假设带来的消极影响。假设输入空间
是n维向量的集合,输出空间为类别标签集合
. 用
表示输入空间
上的随机向量,其中
表示数据集中的第i个特征,用Y表示输出空间
上的随机变量。算法的各参数具体定义如下:
算法输入:数据集:
;待分类实例:
;
算法输出:类标签预测结果:
1) 根据数据集信息计算各属性的权重,为待分类实例中的每一个属性值分配相应的权重值:
(7)
2) 计算在特定类别下各属性值的加权条件概率:
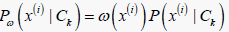 (8)
(8)
3) 根据贝叶斯判定准则,对待分类实例的类标签进行预测:
(9)
其中,
为待分类实例中属性
的取值。
在实际任务中,给定训练集,可将加权朴素贝叶斯分类器中涉及的各权重值以及所有概率估计值计算出来并存储在模型中,待到需要对实例进行预测时,只需要进行简单的计算便能得到分类结果,从而大大提高预测速度。
2.3. 加权k近邻方法
k近邻方法是一种常用的监督学习方法。k近邻方法是懒惰学习算法中的一种,只有在输入待分类实例后,算法才会开始运行,训练时间开销为零。算法通过距离函数来计算两两实例间的距离,从而确定待分类实例的k个最近邻样本点,最后根据决策规则来判断待分类实例的类标签。k的取值不同,分类结果会有显著不同;其次,采用不同的距离计算方式,找出的近邻也可能存在显著差异,从而导致分类结果有显著不同 [7]。本文采用欧氏距离作为实例点之间的距离度量,采用多数表决规则来确定待分类实例的类别标签。
本文提出的加权k近邻方法将加权和引入欧氏距离函数的计算中,通过
(10)
来计算实例
与实例
之间的距离:
其中,
(11)
算法输入:待分类的实例
;数据集
算法输出:实例x的类别y。
1) 通过加权欧氏距离
的计算结果找出训练集T中与实例x最近邻的k个样本点,
确定这k个点 邻域
;
2) 在
中根据多数表决规则决定待分类实例x的类别标签y:
(12)
其中,
为指示函数,条件成立时函数取值为1,反之取值为0。
加权k近邻方法简单直观,在确定k值、距离度量和分类决策规则后,待分类实例的预测类标签唯一确定。
3. 实验及结果
3.1. 数据集及实验步骤
本文选用威斯康星乳腺癌数据集 [8] (Wisconsin Breast Cancer Database: WBCD)进行实验,该数据集总共有699个实例,除类别标签外还包含其他9个特征属性,列举在表1中。根据类标签的不同,该数据集可以划分为241个恶性肿瘤实例和458个良性肿瘤实例。除此之外,该数据集还包含16个有缺失值的样本,在进行实验之前,本文首先将这16个实例删除,实验仅采用剩余的683个完整实例,包括239个恶性肿瘤样本和444个良性肿瘤样本。具体实验步骤如下:
1) 首先采用传统的机器学习方法:朴素贝叶斯分类器、k近邻方法,对数据集进行分类,得到相应算法的分类准确率。
2) 其次,采用本文提出的各类加权机器学习方法:加权朴素贝叶斯分类器、加权k近邻方法再次进行分类,同样以分类准确率作为评价指标。
3) 最后,通过比较这两种传统机器学习方法与其相应的加权方法在分类准确率方面的差异来对本文提出的加权机器学习方法的性能进行评估并借此验证本文加权方法的实用性。

Table 1. Features description in Wisconsin breast cancer database
表1. 威斯康星乳腺癌数据集属性描述
3.2. 实验结果
对于朴素贝叶斯分类器以及本文提出的加权朴素贝叶斯,采用不同折数的交叉验证来进行实验,并计算了各折交叉验证下的分类精度以及平均精度来进行算法性能评估。例如,五折交叉验证首先将数据集划分为5个子集,依次选择5个子集中的一个作为测试集,其他4个子集组成的合集作为训练集。因此,作为测试集的每折数据都有一个分类准确度,这些准确度的平均值作为相应交叉验证下的分类精度。实验结果统计在表2中。

Table 2. Classification accuracies (%) for Naïve Bayes
表2. 朴素贝叶斯分类器的分类准确率
从实验结果可以看出,本文提出的加权朴素贝叶斯模型在分类准确率方面的表现与传统的朴素贝叶斯分类器相当,平均分类精度都为97.13%。尽管朴素贝叶斯分类器中的条件独立性假设在很多现实数据集中都不成立,但其在实际应用中的表现极佳,是机器学习方法中最有力的分类工具之一。本文提出的方法虽然没有提高其分类精度,但从实验结果也可以看出本文基于互信息的加权方法并不会对本来稳健的分类器造成消极影响,因此本文的加权方法对此类机器学习方法具有一定普适性。
对于k近邻方法以及相应的加权k近邻方法,由于其作为一种惰性学习算法的特性,不存在训练模型,从而不适用于交叉验证。k近邻方法会事先存储整个数据集,待到有待分类实例输入后才会开始进行分类任务。代替使用交叉验证,本文采用不同的k值来进行相关实验,每个k值都对应一个分类准确度,同时本文还计算了平均分类精度。具体实验结果见于表3。

Table 3. Classification accuracies (%) for k-NN
表3. k近邻方法的分类准确率
从上述实验结果可以看出,对于每一个不同的k值,本文提出的加权方法对分类准确率都有提高,加权模型的最高分类精度达到92.49%,比相应k值下的传统模型最高提升了3%的准确率。此外,传统k近邻方法的平均分类精度为89.67%,而本文提出的加权模型的平均分类精度达到92.13%,平均提高了2.46%的分类精度。因此,可以得出本文提出的加权k近邻模型在分类准确率方面的表现优于传统方法这一结论,从而也可以证明本文提出的互信息加权方法的合理性以及实用性。
4. 结论
为了解决分类问题中的属性加权问题,为不同属性赋予相应合适权重,以提高分类模型的分类准确率。本文提出了一种基于互信息的属性加权方法,并在两种经典的机器学习方法上进行了实验。将加权模型与传统模型在准确率方面的表现进行了比较。
本文的实验结果表明,我们提出的两个加权模型与传统模型相比表现相当或者更好。同时,值得一提的是,朴素贝叶斯被认为是最简单但功能最强大的分类方法之一 [2]。这可能是本文的加权朴素贝叶斯分类模型与传统方法表现一样好的原因之一,需要进一步的研究来分析造成这一结果的详细原因。对于k近邻方法,实验结果表明,本文提出的加权k近邻模型的性能优于传统规则。由于k近邻规则是非参数分类器,因此本文提出的加权模型可以应用于任何数据集 [9]。
通过实验,本文验证了基于互信息的加权方法用于机器学习模型的有效性。这种方法有以下优点:
首先,该方法以信息论为基础,权重的度量结果可信赖。
其次,该方法不会对自身稳健的分类器造成负面影响,因此具有一定普适性。
再次,该方法可以提高传统分类器的分类准确率,从而可以在实际应用中发挥重要作用。
最后,虽然该加权方法在分类准确率方面的表现良好,但其在分类效率方面的表现还有待进一步研究。
基金项目
国家自然科学基金资助项目(No. 11571009)。