1. 引言
列车运行过程中会受到各种激励,如轮轨激励、气动载荷激励等,由此引发的车辆振动与噪声问题已成为研究人员日益关注的问题。因此,对车辆动态特性的研究,有利于提高整车乘坐舒适性、安全性以及使用寿命 [1]。
轮对作为轨道车辆的重要走形部件,对车辆动力学研究起着关键性的作用。其结构的动态特性通常采用固有频率、阻尼比和振型等参数来描述,即所谓的模态参数 [2]。振动系统的模态特性不仅大大简化了复杂结构的动力分析,而且恰当地描述了系统整体的、固有的动态特性,具有明显的物理意义 [3]。
本文采用试验模态法对自由状态以及钢轨约束状态下的轮对结构进行测试研究,确定其模态频率与振型;对自由状态下的轮对进行仿真计算,建立仿真计算与试验结果能够互相吻合校验的轮对数值模型。
2. 轮对模态试验
轮对模态试验采用多参考点锤击法,分别测试自由状态以及钢轨约束状态下轮对的模态频率与模态振型。
2.1. 试验方法
此次试验共布置33个测点,使其能够描述轮对的基本几何轮廓,根据实际尺寸建立如图1所示的测试几何模型。试验在点1和点12设置两处锤击参考点,分别对轮对施加垂向和横向激励。
轮对自由模态试验使用弹性较好的橡胶减振堆以及弹簧阻尼减振器支撑轮对,如图2(a)所示;轨道约束模态试验是将轮对直接置于钢轨上,并使用铁楔固定车轮,防止轮对在敲击过程中发生微小的转动,如图2(b)所示。
试验在33个测点处布置三轴向振动加速传感器,测试轮对垂向和横向响应,共计66个测试自由度。测试采样频率为4096 Hz,分析数据采用10次敲击结果的平均值。
2.2. 试验数据校验
(1) 频响校验:
图3为经信号处理后得到的激励位置12点(垂向)处的频率响应函数的相位(Phase)和幅值(Mag)图,表现出了较为明显的原点性质。
(2) 相干性校验:
图4中显示了典型测点的频响及相应的相干函数(Coherence)图,除了以刚体模态为主的低频段和信噪比较低的反共振段,在大部分频段上相干函数幅值均接近于1。
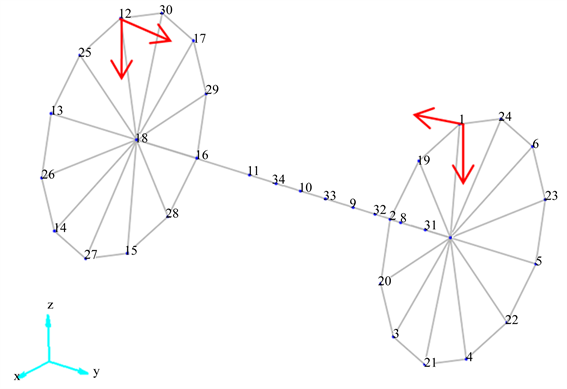
Figure 1. Geometry model of the wheelset for modal test
图1. 轮对模态测试几何模型
 (a)
(a)  (b)
(b)
Figure 2. Field layout of wheelset modal test. (a) Elastic support; (b) Rail-constraint
图2. 轮对模态测试现场布置图。(a) 弹性支持状态;(b) 钢轨约束状态
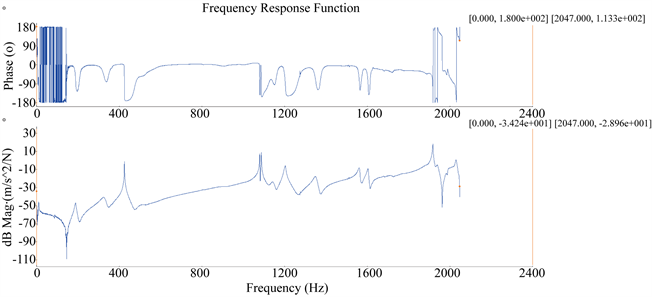
Figure 3. Typical frequency response function (phase and amplitude)
图3. 典型频率响应函数(相位及幅值)
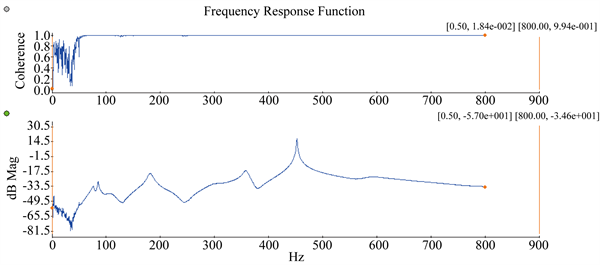
Figure 4. Coherence function and amplitude of FRF
图4. 相干函数及频响幅值
(3) 互异性校验:
图5为跨点频率响应函数的互异性检验,可见在整个频段内,频响函数的互异性良好。
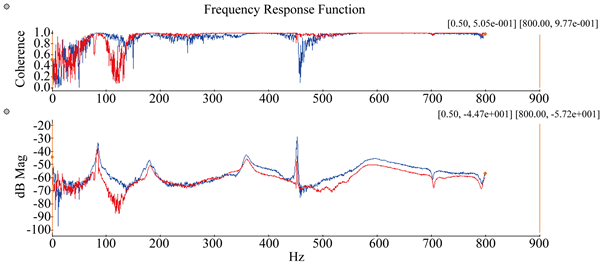
Figure 5. Coincident validation of FRF
图5. 频响函数一致性检验
2.3. 模态辨识结果
试验采用PolyMAX法作为模态识别方法,PolyMAX法是近些年发展起来的频域分析算法,该方法也称为多参考点最小二乘复频域算法 [4]。其识别步骤与最小二乘复指数法(LSCE)很类似。LSCE法是一种时域分析方法,在处理频率较高且模态密集的系统时易产生虚假模态,其稳态图较混乱,模态定阶较难,效果较差,难以取得教理想的结果。而PolyMAX方法的主要好处:一是奇异值求解能避免留数的分解,密集空间可以分离出来。二是该方法既适用于弱阻尼,也适用于强阻尼,密集模态系统的参数识别。三是在强阻尼、密集模态情况下,仍可获得非常清晰的稳态图,从而很容易实现物理模态定阶,结果的客观性更好 [5]。
表1对比了自由状态和钢轨约束状态下的轮对典型模态频率与振型。从表中可知,轮对垂向一阶弯曲和二阶弯曲的约束模态频率高于自由状态下的测试频率,原因是由于轮轨接触,轨道给轮对施加了附加刚度,导致轮对自振频率提高;而在高频范围内(400 Hz以上),轨道附加刚度对车轮的局部模态影响较小,车轮的弯曲以及扭转模态在两种测试工况下,结果基本一致。

Table 1. Modal identification results of wheelset
表1. 轮对的模态识别结果
轨道的附加刚度同时会影响轮对的刚体模态,表2为钢轨约束状态的轮对低阶刚体模态,47.6 Hz为轮对沿轮轨接触点的横摆模态,128.6 Hz轮对绕质心的侧滚模态。研究轮轨接触状态的刚体模态有助于加深对轮对在现车运用条件下动态特性的理解。

Table 2. Rigid body modal frequencies and modal shapes of the wheelset under track-constraint
表2. 钢轨约束状态下轮对的刚体模态频率及振型
3. 模态参数的数值求解与相关性分析方法
3.1. 模态参数的数值求解方法
模态有限元分析的实质就是求解具有有限自由度的无阻尼及无外载荷状态下的运动方程的特征值和特征向量,系统的无阻尼自由振动方程的矩阵表达式为:
(1)
这是一个其次线性微分方程组,其一般解可以由n个特解的线性组合来表示。
令其特解为:
(2)
式中,
为各坐标振幅组成的n阶列阵。此特解便是系统内各个坐标偏离平衡位置时,均以同一频率ω和同一初相角φ作不同振幅的简谐振动。将式(2)带入式(1)并消去公因子
,得到矩阵
和
的广义本征值方程:
(3)
有非零解的充要条件是系数行列式等于零,即:
(4)
由于方程组(3)中只有
行是独立的,因此,只能求得每个振型
中各点位移的相对值。以第一个自由度的位移作为基数,可得到规格化的振型向量
,通常所说的特征值是指结构的各阶固有频率ω,特征向量就是对应某个振动频率的模态振型,公式(5)给出了对特征方程的表达式。
(5)
可见如果结构系统共有n个自由度,那么就可以通过上述方程解得n个特征值和特征向量。
3.2. 模态参数的相关性分析
进行模态参数相关性分析,能够更加准确的确定仿真计算结果与试验测试结果的对应关系(例如模态匹配)以及误差准则。
对模态频率进行校验的常用方法是将计算结果和试验结果分别作为横坐标和纵坐标,在坐标系上标出匹配后的各阶模态频率。如果仿真与试验结果吻合较好,则所有的点应该落在45˚线上。如果大部分的点落在另一斜线附近,则有限元模型的材料参数可能存在误差。
对于模态振型的仿真试验校验,除了观察振型外,还可以利用数值的手段,例如模态比例因子(Modal Scale Factor, MSF)和模态置信度(Modal Assurance Criterion, MAC)。本文使用模态置信度评价方法。
模态置信度,也称为振型相关系数,是一个间于0~1之间的标量,如两个振型向量的MAC值为1,则说明两个振型向量代表的是同一阶模态,为0则代表不同模态。实际运用时,MAC是一个矩阵,好的相关性要求MAC矩阵的对角元 > 70%,非对角元 < 10%。
振型相关系数通常采用以下定义:
(6)
其中,
代表试验模型第i阶振型与有限元模型的第j阶振型之间的相关系数;
代表试验模型的第i阶振型;
是有限元分析模型的第j阶振型;T代表共轭转置。
4. 轮对自由模态试验仿真分析
4.1. 轮对有限元数值模型
轮对有限元模型与模态分析的思路是保证整体质量以及局部刚度、质量分布,保证网格均匀。具体处理方法是:(1) 轮对有限元网格采用六面体实体单元划分;(2) 利用网格节点重合法等效轮轴的过盈配合;(3) 将齿轮箱箱体及内部齿轮的质量等效为一集中质量点,保证质量点的位置与齿轮箱质心一致,并将其通过刚体单元连接在轮轴相应位置;(4) 忽略轴端轴承内部细节,保证其质量、刚度与实际情况一致 [6]。
最终用于模态分析的轮对有限元模型约有2万个节点,1.7万个单元,如图6所示。模态有限元求解采用Lanczos求解器,计算自由状态下的模态频率与模态振型。
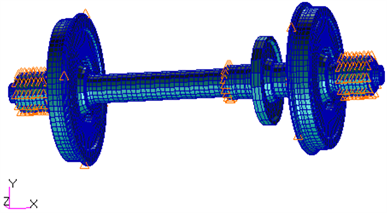
Figure 6. Finite element model of wheelset
图6. 轮对有限元模型
4.2. 试验仿真校验
在对试验和仿真结果进行校核之前,首先需进行节点坐标匹配,即基于试验测点位置对有限元模型的节点进行缩聚。然后以试验测得的轮对自由状态下的7阶典型模态为基准,选择有限元模型的对应模态与其匹配,并计算两者振型相关系数MAC,表3为试验与仿真MAC值匹配表,通过MAC值分析,可知试验与仿真模态振型匹配性较好,从中还可看出,有限元计算的模态阶数多于试验测试的阶数,说明试验测试只得到了轮对的部分模态。
选取4阶典型模态的试验与仿真振型对比如表4所示,其中蓝色框架为有限元模型,内部红色线条为试验模型。从图中也可以直观的看出,仿真与试验的模态振型一致性较好。

Table 3. MAC value matching table
表3. MAC值匹配顺序表

Table 4. Matching results of test and numerical modal
表4. 试验与计算振型匹配结果
基于试验测试和仿真计算的模态振型匹配结果,可以获得其对应的模态频率,见表5。比较结果表明,轮对的低阶模态频率(400 Hz以下),试验测试结果数值普遍大于仿真计算结果,原因是在于试验过程中,支撑轮对用的橡胶减振堆以及弹簧阻尼减振器刚度较大,导致轮对系统引入附加刚度;400 Hz以上,随着频率的提高,附加刚度对于高频模态分布的影响逐渐减小,试验测得的轮对固有频率与仿真计算得到的频率一致性较好,说明所建立的有限元模型能够很好地反映实际结构的振动特性 [7] [8] [9]。


Table 5. Modal identification results of wheelset
表5. 轮对的模态识别结果
5. 结语
本文测试分析了自由边界条件以及轨道约束条件下,轨道车辆轮对结构的典型模态频率与模态振型,试验结果表明,轨道约束对于低频段(400 Hz以下)轮轴一阶弯曲和二阶弯曲的模态频率影响较大,对于高频段(400 Hz以上),车轮的弯曲、扭转以及轮轴的高阶模态频率影响较小。另外,本文基于有限元模态分析基本理论,建立了轮对的模态分析有限元模型,并计算了其在自由状态下振动模态。通过MAC数值分析方法,证明所建有限元模型的计算结果与模态试验结果吻合较好,可以作为后续车辆结构设计及优化的理论依据。