潜伏期具有传染性的水痘模型的分析

Analysis of a Varicella Model Incorporating Infectious Force in Latent Period

摘要: 研究了一类潜伏期具有传染性的水痘模型，并考虑复发，隔离以及接种疫苗的因素。得到了水痘模型的基本再生数，利用李雅普诺夫第二方法证明水痘模型的全局动力学性态完全由基本再生数所控制。即当基本再生数小于1时，水痘病毒会在人群中逐渐消失；当基本再生数大于1时，水痘病毒不会绝灭并且在人群中形成地方病。

Abstract: A varicella model with infectious force during the latent period has been considered with the factors of relapse, quarantine and vaccination taken into account. The basic reproduction number of the varicella model is obtained, and the varicella model’s global dynamics are completely controlled by the basic reproduction number by using the second method of Lyapunov. If the basic reproduction number is under one, the varicella virus gradually disappears in the population; while if the basic reproduction number is above one, the varicella virus does not eradicate and becomes an endemic disease in the population.

1. 引言

水痘是一种由带状疱疹病毒引发的呼吸道传染病，具有较强的传染性，严重时会引起肺炎、病毒性脑炎等疾病。水痘病毒主要通过空气飞沫、直接接触进行传播，它的平均潜伏期约两周。水痘一直是我国儿童发病率居前列的传染病，常在儿童学校或儿童集体场所爆发或流行 [1]，但目前没有较好的应对措施，因此受到全社会的共同关注。

疫苗接种可以降低水痘的发生率，目前中国陆续有城市将水痘疫苗的接种范围进行扩大，对儿童实现了更好的预防保护。由于水痘具有潜伏期，且潜伏期末具有传染性，传播途径较多以及传播性较强，更重要的是没有针对性的药物，只能依靠自身的自愈性以及服用抗病毒的药物得以痊愈，从而使得水痘疾病的治疗工作进展缓慢，对健康儿童的威胁较大。另外有一些病人在痊愈之后，由于机体免疫能力下降，潜伏在机体内的水痘病毒经过重新活化之后会导致再次发病。人群中一旦发现水痘病人，要尽快将病人进行隔离，避免病人与健康人群进行接触。

对于水痘传染病，国内外已经有一些关于水痘模型的研究，但是仅有少量关于水痘传播的动力学研究。文献 [2] 对连续水痘模型进行离散化处理，根据水痘的潜伏期长短和传染期状况建立离散模型，对比不同控制措施的发病人数进行控制效果的评价。文献 [3] 建立了浙江省水痘传播动力学模型，预测未来水痘病例发生情况，比较水痘疫苗不同免疫策略的成本和效益。文献 [4] 考虑了人口流动、季节性等诸多因素，讨论了水痘长期的流行趋势。基于以上的一些原因，本文考虑了潜伏期具有传染性、疫苗接种、隔离以及复发等因素，建立一个水痘动力学模型，通过应用李雅普诺夫第二方法构造李雅普诺夫函数分析模型的动力学性态。

2. 建立模型

在本文中，总人口由六类人构成：t时刻的易感者类 $\left(S\left(t\right)\right)$，t时刻的疫苗接种者类 $\left(V\left(t\right)\right)$，t时刻的潜伏者类 $\left(E\left(t\right)\right)$，t时刻的水痘病人 $\left(I\left(t\right)\right)$，t时刻的隔离者类 $\left(Q\left(t\right)\right)$ 和t时刻的恢复者类 $\left(R\left(t\right)\right)$。 $V\left(t\right)$ 描述的是幼儿接种疫苗后的变化情况，疫苗有效接种者获得抗体保护后，随着时间的流逝抗体会逐渐衰减，直至消失，然后疫苗接种者进入易感者类；易感者类 $S\left(t\right)$ 的个体被水痘患者感染后，会转化为水痘病毒携带者，进入潜伏者类，且具有传染性；潜伏者类 $E\left(t\right)$ 的个体渡过潜伏期，会出现临床症状，转化为水痘病人；病人康复后获得免疫力，进入恢复者类；但是随着时间的流逝以及恢复者自身免疫力的降低，恢复者会复发而重新成为水痘病人。 $Q\left(t\right)$ 是描述被隔离的水痘病人，发现水痘病人时，把水痘病人进行隔离治疗。这六类人相互转移的转移框图如图1所示。 $N\left(t\right)$ 表示t时刻的所有人，则有 $N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+Q\left(t\right)+R\left(t\right)$。

人口的输入率用A表示，p是输入人口接种水痘疫苗的比例，而 $\left(1-p\right)$ 表示输入人口未接种水痘疫苗的比例，自然死亡率和因病死亡率分别用 $\mu$ 和d表示， $\xi$ 表示接种疫苗者转化为易感者的转移率， ${\beta }_{\text{1}}$， ${\beta }_{\text{2}}$ 分别表示水痘病人和潜伏者类的传染率系数，k为潜伏者转化为水痘病人的转移率， $\omega$ 是将水痘病人隔离的比率， $r_1$， $r_2$ 是水痘病人和隔离者的治愈率， $\alpha$ 为复发率。根据图1可知，这个模型可以表述为下面的微分方程组：

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\left(1-p\right)A-{\beta }_{1}SI-{\beta }_{2}SE-\mu S+\xi V\hfill \\ \frac{\text{d}V}{\text{d}t}=pA-\left(\mu +\xi \right)V\hfill \\ \frac{\text{d}E}{\text{d}t}={\beta }_{1}SI+{\beta }_{2}SE-\left(\mu +k\right)E\hfill \\ \frac{\text{d}I}{\text{d}t}=kE-\left(\omega +r_1+\mu +d\right)I+\alpha R\hfill \\ \frac{\text{d}Q}{\text{d}t}=\omega I-\left(\mu +d+r_2\right)Q\hfill \\ \frac{\text{d}R}{\text{d}t}=r_{1}I+r_{2}Q-\left(\mu +\alpha \right)R\hfill \end{array}$ (1)

$p=0$ 表示系统(1)没有进行水痘疫苗的接种， $p=1$ 表示完全进行水痘疫苗接种，本文考虑一般情况，

所以p取 $p\in \left(0,1\right)$ [5]。由模型(1)的第二个式子显然有：当 $t\to \infty$ 时， $V\to V_0$， $V_0=\frac{pA}{\xi +\mu }$，由于S，E，I，Q，R未在V的方程中出现，所以可以得到以下的等价系统：

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\left(1-p\right)A+A_0-{\beta }_{1}SI-{\beta }_{2}SE-\mu S\hfill \\ \frac{\text{d}E}{\text{d}t}={\beta }_{1}SI+{\beta }_{2}SE-\left(\mu +k\right)E\hfill \\ \frac{\text{d}I}{\text{d}t}=kE-\left(\omega +r_1+\mu +d\right)I+\alpha R\hfill \\ \frac{\text{d}Q}{\text{d}t}=\omega I-\left(\mu +d+r_2\right)Q\hfill \\ \frac{\text{d}R}{\text{d}t}=r_{1}I+r_{2}Q-\left(\mu +\alpha \right)R\hfill \end{array}$ (2)

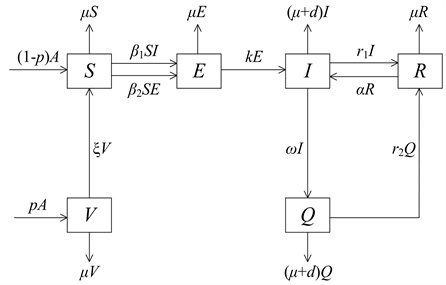
Figure 1. The schematic diagram of a varicella model with infectious force in latent period

图1. 潜伏期具有传染性的水痘模型的转移框图

其中 $A_0=\frac{\xi p}{\mu +\xi }A$。

因为微分方程组(2)的等号右端关于因变量是连续并且可微的，所以由微分方程组解的存在唯一性定理可知：经过初始值点 ${\left(S^0,E^0,I^0,Q^0,R^0\right)}^{\text{T}}\in R_{+}^5$ 的解是存在且唯一的；进一步由定理5.2.1 [6] 可知：经过初始值点 ${\left(S^0,E^0,I^0,Q^0,R^0\right)}^{\text{T}}\in R_{+}^5$ 的解是非负的。利用模型(1)有

$N^{\prime }=\left(1-p\right)A+A_0-\mu N-d\left(I+Q\right)\le \left(1-p\right)A+A_0-\mu N$

即有 $\underset{t\to \infty }{\lim }N\left(t\right)\le S_0$，其中 $S_0=\frac{\left(1-p\right)A+A_0}{\mu }$，所以 $N\left(t\right)$ 是最终有界的，从而 $S\left(t\right)$， $E\left(t\right)$， $I\left(t\right)$， $Q\left(t\right)$，

$R\left(t\right)$ 都是有界函数，且模型(2)在区域 $\Phi$ 中是正不变的，其中

$\Phi =\left\{{\left(S,E,I,Q,R\right)}^{\text{T}}\in R_{+}^5:S\le S_0,S+E+I+Q+R\le S_0\right\}$。

3. 基本再生数及平衡点的稳定性

模型(2)总是存在无病平衡点 $P_{\text{0}}={\left(S_0,0,0,0,0\right)}^{\text{T}}$。由文献 [7] 可知染病仓室为E, I, Q, R，故可得

$F=\left(\begin{array}{cccc}{\beta }_2{S}_{\text{0}}& {\beta }_1{S}_{\text{0}}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$

$V=\left(\begin{array}{cccc}\mu +k& 0& 0& 0\\ -k& \omega +r_1+\mu +d& 0& -\alpha \\ 0& -\omega & \mu +d+r_2& 0\\ 0& -r_1& -r_2& \mu +\alpha \end{array}\right)$

利用文献 [8] 中再生矩阵的方法可以计算系统(2)的基本再生数 $R_0$，即得 $R_{\text{0}}=\rho \left(F{V}^{-1}\right)$，其中 $\rho \left(M\right)$ 为矩阵 $M$ 的谱半径，所以求得基本再生数为：

$R_0=\frac{1}{\mu +k}\left[{\beta }_2{S}_{\text{0}}+{\beta }_1{S}_{\text{0}}k\frac{\left(\mu +d+r_2\right)\left(\mu +\alpha \right)}{\left(\omega +r_1+\mu +d\right)\left(\mu +d+r_2\right)\left(\mu +\alpha \right)-\alpha \omega r_2-\alpha r_1\left(\mu +d+r_2\right)}\right]$ (3)

接下来说明地方病平衡点的存在性。

定理1 如果基本再生数大于1，微分方程组(2)仅有一个地方病平衡点 $P_{*}={\left(S_{*},E_{*},I_{*},Q_{*},R_{*}\right)}^{\text{T}}$， $S_{\ast }=\frac{S_{\text{0}}}{R_0}$， $E_{\ast }=\frac{\mu S_0}{\mu +k}\left(1-\frac{1}{R_0}\right)$， $I_{\ast }=\frac{\left[\left(\mu +k\right)R_0-{\beta }_2{S}_0\right]E_{\ast }}{{\beta }_{\text{1}}{S}_{\text{0}}}$， $Q_{\ast }=\frac{\omega }{\mu +d+r_2}{I}_{*}$， $R_{\ast }=\frac{r_1{I}_{*}+r_2{Q}_{*}}{\mu +\alpha }$。

证明：显然系统(2)的地方病平衡点满足以下的代数方程组

$\{\begin{array}{l}{A}_1={\beta }_1{S}_{\text{*}}{I}_{\text{*}}+{\beta }_2{S}_{\text{*}}{E}_{\text{*}}+\mu S_{\text{*}}\hfill \\ {\beta }_1{S}_{\text{*}}{I}_{\text{*}}+{\beta }_2{S}_{\text{*}}{E}_{\text{*}}=\left(\mu +k\right)E_{\text{*}}\hfill \\ \left(\omega +r_1+\mu +d\right)I_{\text{*}}-\alpha R_{\text{*}}=k{E}_{\text{*}}\hfill \\ \left(\mu +d+r_2\right)Q_{\text{*}}=\omega I_{\text{*}}\hfill \\ r_1{I}_{\text{*}}+r_2{Q}_{\text{*}}=\left(\mu +\alpha \right)R_{\text{*}}\hfill \\ A_1=\left(1-p\right)A+A_0\hfill \end{array}$ (4)

由(4)的第四式可得

$Q_{\text{*}}=\frac{\omega }{\mu +d+r_2}{I}_{\text{*}}$ (5)

将(5)式代入(4)的第五式得

$R_{\text{*}}=\left[\frac{r_1}{\mu +\alpha }+\frac{r_2\omega }{\left(r_2+d+\mu \right)\left(\mu +\alpha \right)}\right]I_{\text{*}}$ (6)

将(6)式代入(4)的第三式，整理得

$E_{\text{*}}=\frac{1}{k}\left[\left(\omega +r_1+\mu +d\right)-\frac{\alpha r_1}{\mu +\alpha }-\frac{\alpha r_2\omega }{\left(r_2+d+\mu \right)\left(\mu +\alpha \right)}\right]I_{\text{*}}$ (7)

将(7)式代入(4)的第二式，经过简单计算得

$S_{\text{*}}=\frac{S_0}{R_0}$ (8)

将(8)代入(4)式可得 $E_{\ast }=\frac{\mu S_0}{\mu +k}\left(1-\frac{1}{R_0}\right)$， $I_{\ast }=\frac{\left[\left(\mu +k\right)R_0-{\beta }_2{S}_0\right]E_{\ast }}{{\beta }_{\text{1}}{S}_{\text{0}}}$， $R_{\ast }=\frac{r_1{I}_{*}+r_2{Q}_{*}}{\mu +\alpha }$， $Q_{\ast }=\frac{\omega }{\mu +d+r_2}{I}_{*}$，因为 $R_0>1$，所以可以判断 $E_{*}>0$， $I_{*}>0$， $R_{*}>0$， $Q_{*}>0$，所以系统(2)仅有一个地方病平衡点。

接下来通过李雅普诺夫第二方法说明平衡点的稳定性。

定理2 如果基本再生数小于1，系统(2)的无病平衡点是全局渐近稳定的，且吸引从 $\Phi$ 中出发的所有解并且水痘病毒将从人群中消失。

证明：当基本再生数 $R_{\text{0}}<1$ 时，构造如下的李雅普诺夫函数

$V_1=E+BI+CQ+DR$

其中 $B=\frac{\mu +k-{\beta }_{2}S}{k}$， $C=\frac{r_2}{\mu +d+r_2}D$， $D=\frac{\alpha }{\mu +\alpha }B$。

$V_1$ 沿着系统(2)的解求全导数得

$\frac{\text{d}{V}_1}{\text{d}t}=\frac{\text{d}E}{\text{d}t}+B\frac{\text{d}I}{\text{d}t}+C\frac{\text{d}Q}{\text{d}t}+D\frac{\text{d}R}{\text{d}t}$

将模型(2)各分量代入上式并整理可得

$\begin{array}{c}\frac{\text{d}{V}_1}{\text{d}t}={\beta }_{1}SI+{\beta }_{2}SE-\left(\mu +k\right)E+B\left[kE-\left(\omega +r_1+\mu +d\right)I+\alpha R\right]\\ +C\left[\omega I-\left(\mu +d+r_2\right)Q\right]+D\left[r_{1}I+r_{2}Q-\left(\mu +\alpha \right)R\right]\\ =\left[{\beta }_{1}S-B\left(\omega +r_1+\mu +d\right)+C\omega +D{r}_1\right]I\\ +\left[{\beta }_{2}S+Bk-\left(\mu +k\right)\right]E+\left[D{r}_2-C\left(\mu +d+r_2\right)\right]Q\\ +\left[B\alpha -D\left(\mu +\alpha \right)\right]R\end{array}$

将B，C，D代入上面的式子可求得

$\begin{array}{c}\frac{\text{d}{V}_1}{\text{d}t}=\left[{\beta }_{1}S+B\frac{\omega r_2\alpha }{\left(\mu +\alpha \right)\left(\mu +d+r_2\right)}+B\frac{\alpha r_1}{\mu +\alpha }-B\left(\omega +r_1+\mu +d\right)\right]I\\ ={\beta }_{1}SI+\frac{\left(\mu +k\right)-{\beta }_{2}S}{k}\left[\frac{-\alpha \omega r_2+\alpha r_1\left(\mu +d+r_2\right)}{\left(\mu +\alpha \right)\left(\mu +d+r_2\right)}+\left(\omega +r_1+\mu +d\right)\right]I\\ \le \left[{\beta }_1{S}_0+\frac{\left(\mu +k\right)-{\beta }_2{S}_0}{k}\frac{-{\beta }_1{S}_{0}k}{\left(\mu +k\right)R_0-{\beta }_2{S}_0}\right]I\\ ={\beta }_1{S}_0\left[1+\frac{-\left(\mu +k\right)+{\beta }_2{S}_0}{\left(\mu +k\right)R_0-{\beta }_2{S}_0}\right]I\\ ={\beta }_1{S}_0\frac{\left(R_0-1\right)\left(\mu +k\right)}{\left(\mu +k\right)R_0-{\beta }_2{S}_0}I\le 0\end{array}$

当且仅当 $I=\text{0}$，等号才成立。文献 [9] 表明：系统(2)的每个解的极限集都包含在集合 $\left\{{\left(S,E,I,Q,R\right)}^{\text{T}}\in R_{+}^5:I=0\right\}$ 的最大不变集中，此时最大不变集是 $P_0$，从而 $P_0$ 是全局渐近稳定的，吸引从 $\Phi$ 中出发的所有解，并且经过时间的流逝水痘病毒会从人群中根除。

定理3 如果基本再生数大于1，无病平衡点 $P_0={\left(S_0,0,0,0,0\right)}^{\text{T}}$ 是不稳定的。

证明：令 $h=S-S_0$ 代入(2)的前两式可求得

$\begin{array}{c}\frac{\text{d}h}{\text{d}t}=\frac{\text{d}S}{\text{d}t}=\left(1-p\right)A+A_0-{\beta }_1\left(S_0+h\right)I-{\beta }_2\left(h+S_0\right)E-\mu \left(h+S_0\right)\\ =(1-p)A+A_0-\mu S_0-\mu h-{\beta }_1{S}_{0}I-{\beta }_2{S}_{0}E-{\beta }_{1}hI-{\beta }_{2}hE\\ =-\mu h-{\beta }_1{S}_{0}I-{\beta }_2{S}_{0}E-{\beta }_{1}hI-{\beta }_{2}hE\end{array}$ (9)

$\begin{array}{c}\frac{\text{d}E}{\text{d}t}={\beta }_1\left(S_0+h\right)I+{\beta }_2\left(h+S_0\right)E-\left(\mu +k\right)E\\ ={\beta }_1{S}_{0}I+\left[{\beta }_2{S}_0-\left(\mu +k\right)\right]E+{\beta }_{1}hI+{\beta }_{2}hE\end{array}$ (10)

模型(2)在无病平衡点 $P_0={\left(S_0,0,0,0,0\right)}^{\text{T}}$ 处的线性化系统 [10] 为

$\{\begin{array}{l}\frac{\text{d}h}{\text{d}t}=-\mu h-{\beta }_1{S}_{0}E-{\beta }_1{S}_{0}I\hfill \\ \frac{\text{d}E}{\text{d}t}={\beta }_1{S}_{0}I+\left[{\beta }_2{S}_0-\left(\mu +k\right)\right]E\hfill \\ \frac{\text{d}I}{\text{d}t}=-\left(\omega +r_1+\mu +d\right)I+kE+\alpha R\hfill \\ \frac{\text{d}Q}{\text{d}t}=\omega I-\left(\mu +d+r_2\right)Q\hfill \\ \frac{\text{d}R}{\text{d}t}=r_{1}I-\left(\mu +\alpha \right)R+r_{2}Q\hfill \end{array}$ (11)

由(10)式的微分方程组可得其系数矩阵为

$A=\left(\begin{array}{ccccc}-\mu & -{\beta }_{\text{2}}{S}_{\text{0}}& -{\beta }_{\text{1}}{S}_{\text{0}}& \text{0}& \text{0}\\ \text{0}& {\beta }_{\text{2}}{S}_{\text{0}}-\left(\mu +k\right)& {\beta }_{\text{1}}{S}_{\text{0}}& 0& 0\\ 0& k& -\left(\omega +r_1+\mu +d\right)& 0& \alpha \\ 0& 0& \omega & -\left(\mu +d+r_2\right)& 0\\ 0& 0& r_1& r_2& -\left(\mu +\alpha \right)\end{array}\right)$

系数矩阵A对应的特征多项式为

$\phi \left(\lambda \right)=\left|\begin{array}{ccccc}\lambda +\mu & {\beta }_{\text{2}}{S}_{\text{0}}& {\beta }_{\text{1}}{S}_{\text{0}}& \text{0}& \text{0}\\ \text{0}& \lambda -{\beta }_{\text{2}}{S}_{\text{0}}+\left(\mu +k\right)& -{\beta }_{\text{1}}{S}_{\text{0}}& \text{0}& \text{0}\\ \text{0}& -k& \lambda +\left(\omega +r_1+\mu +d\right)& 0& -\alpha \\ 0& 0& -\omega & \lambda +\left(\mu +d+r_2\right)& \text{0}\\ \text{0}& \text{0}& -r_1& -r_2& \lambda +\left(\mu +\alpha \right)\end{array}\right|$

现令 $\lambda =0$，代入特征多项式 $\phi \left(\lambda \right)$ 可得

$\begin{array}{c}\phi \left(\text{0}\right)=\left|\begin{array}{ccccc}\mu & {\beta }_{\text{2}}{S}_{\text{0}}& {\beta }_{\text{1}}{S}_{\text{0}}& \text{0}& \text{0}\\ \text{0}& -{\beta }_{\text{2}}{S}_{\text{0}}+\left(\mu +k\right)& -{\beta }_{\text{1}}{S}_{\text{0}}& \text{0}& \text{0}\\ \text{0}& -k& \left(\omega +r_{\text{1}}+\mu +d\right)& 0& -\alpha \\ 0& 0& -\omega & \left(\mu +d+r_{\text{2}}\right)& \text{0}\\ \text{0}& \text{0}& -r_{\text{1}}& -r_{\text{2}}& \left(\mu +\alpha \right)\end{array}\right|\\ =\mu \left[\left(\omega +r_{\text{1}}+\mu +d\right)\left(\mu +d+r_2\right)\left(\mu +\alpha \right)-\alpha \omega r_2-\alpha r_1\left(\mu +d+r_2\right)\right]\left(\mu +k\right)\left(1-R_0\right)\\ <\text{0}\end{array}$

显然当 $\lambda \to +\infty$， $\phi \left(\lambda \right)\to +\infty$，因为特征多项式 $\phi \left(\lambda \right)$ 关于 $\lambda$ 是连续函数。因为 $\phi \left(0\right)<0$，由介值定理可知至少存在一个 ${\lambda }_{\text{0}}>0$，使得 $\phi \left({\lambda }_{\text{0}}\right)=0$，所以 $\phi \left(\lambda \right)=0$ 至少存在一个正根 ${\lambda }_{\text{0}}$，故当 $R_{\text{0}}>1$ 时， $P_{\text{0}}$ 是不稳定的。

定理4 如果基本再生数大于1，系统(2)的地方病平衡点是全局渐近稳定的，水痘病毒不能从人群中消失从而形成地方病。

证明：给出以下形式的李雅普诺夫函数

$V_2=S-S_{*}\ln S+E-E_{*}\ln E+b_2\left(I-I_{*}\ln I\right)+b_3\left(Q-Q_{*}\ln Q\right)+b_4\left(R-R_{*}\ln R\right)$

其中 $b_2=\frac{{\beta }_1{S}_{\ast }{I}_{\ast }}{k{E}_{\ast }}$， $b_3=\frac{r_2{Q}_{\ast }}{\omega I_{\ast }}{b}_4$， $b_4=\frac{\alpha R_{\ast }}{r_1{I}_{\ast }+r_2{Q}_{\ast }}{b}_2$。

$V_2$ 沿着(2)的解求全导数，整理可得

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}=\left(\frac{\text{d}S}{\text{d}t}-\frac{S_{\ast }}{S}\frac{\text{d}S}{\text{d}t}\right)+\left(\frac{\text{d}E}{\text{d}t}-\frac{E_{\ast }}{E}\frac{\text{d}E}{\text{d}t}\right)+b_2\left(\frac{\text{d}I}{\text{d}t}-\frac{I_{\ast }}{I}\frac{\text{d}I}{\text{d}t}\right)+b_3\left(\frac{\text{d}Q}{\text{d}t}-\frac{Q_{\ast }}{Q}\frac{\text{d}Q}{\text{d}t}\right)+b_4\left(\frac{\text{d}R}{\text{d}t}-\frac{R_{\ast }}{R}\frac{\text{d}R}{\text{d}t}\right)\\ =\left(1-\frac{S_{\ast }}{S}\right)\frac{\text{d}S}{\text{d}t}+\left(1-\frac{E_{\ast }}{E}\right)\frac{\text{d}E}{\text{d}t}+b_2\left(1-\frac{I_{\ast }}{I}\right)\frac{\text{d}I}{\text{d}t}+b_3\left(1-\frac{Q_{\ast }}{Q}\right)\frac{\text{d}Q}{\text{d}t}+b_4\left(1-\frac{R_{\ast }}{R}\right)\frac{\text{d}R}{\text{d}t}\\ =\left(1-\frac{S_{\ast }}{S}\right)\left[\left(1-p\right)A+A_0-{\beta }_{1}SI-{\beta }_{2}SE-\mu S\right]+\left(1-\frac{E_{\ast }}{E}\right)\left[{\beta }_{1}SI+{\beta }_{2}SE-\left(\mu +k\right)E\right]\\ +b_2\left(1-\frac{I_{\ast }}{I}\right)\left[kE-\left(\omega +r_1+\mu +d\right)+\alpha R\right]+b_3\left(1-\frac{Q_{\ast }}{Q}\right)\left[\omega I-\left(\mu +d+r_2\right)Q\right]\\ +b_4\left(1-\frac{R_{\ast }}{R}\right)\left[r_{1}I+r_{2}Q-\left(\mu +\alpha \right)R\right]\end{array}$ (12)

在地方病平衡点 $P_{\ast }$ 处有

$\{\begin{array}{l}\left(1-p\right)A+A_0={\beta }_1{S}_{\ast }{I}_{\ast }+{\beta }_2{S}_{\ast }{E}_{\ast }+\mu S_{\ast }\hfill \\ \left(\mu +k\right)=\frac{{\beta }_1{S}_{\ast }{I}_{\ast }+{\beta }_2{S}_{\ast }{E}_{\ast }}{E_{\ast }}\hfill \\ \left(\omega +r_1+\mu +d\right)=\frac{k{E}_{\ast }+\alpha R_{\ast }}{I_{\ast }}\hfill \\ \left(\mu +d+r_2\right)=\frac{\omega I_{\ast }}{Q_{\ast }}\hfill \\ \left(\mu +\alpha \right)=\frac{r_1{I}_{\ast }+r_2{Q}_{\ast }}{R_{\ast }}\hfill \end{array}$ (13)

将(13)式代入(12)式，整理可得

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}=\left(1-\frac{S_{*}}{S}\right)\left[{\beta }_1{S}_{*}{I}_{*}\left(1-\frac{SI}{S_{*}{I}_{*}}\right)+{\beta }_2{S}_{*}{E}_{*}\left(1-\frac{SE}{S_{*}{E}_{*}}\right)+\mu S_{*}\left(1-\frac{S}{S_{*}}\right)\right]\\ +\left(1-\frac{E_{*}}{E}\right)\left[{\beta }_1{S}_{*}{I}_{*}\left(\frac{SI}{S_{*}{I}_{*}}-\frac{E}{E_{*}}\right)+{\beta }_2{S}_{*}{E}_{*}\left(\frac{SE}{S_{*}{E}_{*}}-\frac{E}{E_{*}}\right)\right]\\ +b_2\left(1-\frac{I_{*}}{I}\right)\left[k{E}_{*}\left(\frac{E}{E_{*}}-\frac{I}{I_{*}}\right)+\alpha R_{*}\left(\frac{R}{R_{*}}-\frac{I}{I_{*}}\right)\right]\\ +b_3\left(1-\frac{Q_{*}}{Q}\right)\left[\omega I_{*}\left(\frac{I}{I_{*}}-\frac{Q}{Q_{*}}\right)\right]\\ +b_4\left(1-\frac{R_{*}}{R}\right)\left[r_1{I}_{*}\left(\frac{I}{I_{*}}-\frac{R}{R_{*}}\right)+r_2{Q}_{*}\left(\frac{Q}{Q_{*}}-\frac{R}{R_{*}}\right)\right]\end{array}$ (14)

令 $x=\frac{S}{S_{*}}$， $y=\frac{E}{E_{*}}$， $z=\frac{I}{I_{*}}$， $m=\frac{Q}{Q_{*}}$， $n=\frac{R}{R_{*}}$ 代入(14)可得

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}=\left(1-\frac{1}{x}\right)\left[{\beta }_1{S}_{\ast }{I}_{\ast }\left(1-xz\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(1-xy\right)+\mu S_{\ast }\left(1-x\right)\right]\\ +\left(1-\frac{1}{y}\right)\left[{\beta }_1{S}_{\ast }{I}_{\ast }\left(xz-y\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(xy-y\right)\right]\\ +b_2\left(1-\frac{1}{z}\right)\left[k{E}_{\ast }\left(y-z\right)+\alpha R_{\ast }\left(n-z\right)\right]+b_3\left(1-\frac{1}{m}\right)\left[\omega I_{\ast }\left(z-m\right)\right]\\ +b_4\left(1-\frac{1}{n}\right)\left[r_1{I}_{\ast }\left(z-n\right)+r_2{Q}_{\ast }\left(m-n\right)\right]\end{array}$

$\begin{array}{l}={\beta }_1{S}_{\ast }{I}_{\ast }\left(1-\frac{1}{x}-xz+z\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(1-xy-\frac{1}{x}+y\right)+\mu S_{\ast }\left(1-\frac{1}{x}-x+1\right)\\ +{\beta }_1{S}_{\ast }{I}_{\ast }\left(xz-y-\frac{xz}{y}+1\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(xy-y-x+\text{1}\right)+b_{2}k{E}_{\ast }\left(y-z-\frac{y}{z}+1\right)\\ +b_2\alpha R_{\ast }\left(n-z-\frac{n}{z}+1\right)+b_3\omega I_{\ast }\left(z-m-\frac{z}{m}+1\right)+b_4{r}_1{I}_{\ast }\left(z-n-\frac{z}{n}+1\right)\\ +b_4{r}_2{Q}_{\ast }\left(m-n-\frac{m}{n}+1\right)\end{array}$ (15)

设

$\begin{array}{c}T=\left(-{\beta }_{\text{1}}{S}_{\ast }{I}_{\ast }+{\beta }_{\text{1}}{S}_{\ast }{I}_{\ast }\right)xz+\left(-{\beta }_{\text{2}}{S}_{\ast }{I}_{\ast }+{\beta }_{\text{2}}{S}_{\ast }{I}_{\ast }\right)xy+\left({\beta }_{\text{1}}{S}_{\ast }{I}_{\ast }-b_{2}k{E}_{\ast }-b_2\alpha R_{\ast }+b_3\omega I_{\ast }+b_4{r}_1{I}_{\ast }\right)z\\ +\left({\beta }_{\text{2}}{S}_{\ast }{E}_{\ast }-{\beta }_{\text{1}}{S}_{\ast }{I}_{\ast }-{\beta }_{\text{2}}{S}_{\ast }{E}_{\ast }+b_{2}k{E}_{\ast }\right)y+\left(-b_3\omega I_{\ast }+b_4{r}_2{Q}_{\ast }\right)m+\left(b_2\alpha R_{\ast }-b_4{r}_1{I}_{\ast }-b_4{r}_2{Q}_{\ast }\right)n\end{array}$

由 $b_{\text{2}}$， $b_{\text{3}}$， $b_{\text{4}}$ 的值可知 $T=0$，(15)式等于(16)式与T之和，故

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}={\beta }_1{S}_{\ast }{I}_{\ast }\left(1-\frac{1}{x}\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(1-\frac{1}{x}\right)+\mu S_{\ast }\left(1-\frac{1}{x}-x+1\right)\\ +{\beta }_{\text{1}}{S}_{\ast }{I}_{\ast }\left(\text{1}-\frac{xz}{y}\right)+{\beta }_2{S}_{\ast }{E}_{\ast }\left(\text{1}-x\right)+b_{2}k{E}_{\ast }\left(\text{1}-\frac{y}{z}\right)\\ +b_2\alpha R_{\ast }\left(\text{1}-\frac{n}{z}\right)+b_3\omega I_{\ast }\left(\text{1}-\frac{z}{m}\right)+b_4{r}_1{I}_{\ast }\left(\text{1}-\frac{z}{n}\right)+b_4{r}_2{Q}_{\ast }\left(\text{1}-\frac{m}{n}\right)\end{array}$ (16)

将 $b_{\text{2}}$， $b_{\text{3}}$， $b_{\text{4}}$ 代入(16)式整理可得

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}=b_4{r}_1{I}_{\ast }\left(2-\frac{n}{z}-\frac{z}{n}\right)+b_4{r}_2{Q}_{\ast }\left(3-\frac{n}{z}-\frac{z}{m}-\frac{m}{n}\right)\\ +{\beta }_1{S}_{\ast }{I}_{\ast }\left(3-\frac{1}{x}-\frac{xz}{y}-\frac{y}{z}\right)+\left({\beta }_2{S}_{\ast }{E}_{\ast }+\mu S_{\ast }\right)\left(2-x-\frac{1}{x}\right)\end{array}$

利用算术–几何平均值不等式知

$\begin{array}{c}\frac{\text{d}{V}_2}{\text{d}t}\le b_4{r}_1{I}_{\ast }\left(2-\text{2}\sqrt{\frac{n}{z}\frac{z}{n}}\right)+b_4{r}_2{Q}_{\ast }\left(3-\text{3}\sqrt[3]{\frac{n}{z}\frac{z}{m}\frac{m}{n}}\right)\\ +{\beta }_1{S}_{\ast }{I}_{\ast }\left(3-\text{3}\sqrt[3]{\frac{1}{x}\frac{xz}{y}\frac{y}{z}}\right)+\left({\beta }_2{S}_{\ast }{E}_{\ast }+\mu S_{\ast }\right)\left(2-\text{2}\sqrt{x\frac{1}{x}}\right)\\ \le \text{0}\end{array}$

只有当 $x=\frac{1}{x}=\frac{xz}{y}=\frac{y}{z}$ 与 $\frac{z}{n}=\frac{n}{z}=\frac{z}{m}=\frac{m}{n}$ 时，等号才成立，也即当 $S=S_{\ast }$， $y=z=m=n$ 时，有 $\frac{\text{d}{V}_2}{\text{d}t}\le 0$。

[9] 表明与 $\Phi$ 的内部相交的系统(2)的解的极限集都包含在集合 $\left\{{\left(S,E,I,Q,R\right)}^{\text{T}}\in R_{+}^5:S=S_{\ast }\right\}$ 的最大不变集中，此最大不变集是 $P_{\ast }$，所以此时 $P_{\ast }$ 是全局渐近稳定的，吸引从 $\Phi$ 中出发的所有解，水痘病毒不能在人群中消失，同时形成地方病。

4. 结语

本文考虑疫苗接种，潜伏期具有传染性，恢复者复发，水痘病人隔离这些重要因素，建立了一个水痘动力学模型，说明了模型的解的适定性和有界性。得到了基本再生数，证明了地方病平衡点的存在性并给出显示表达式。其次，通过利用李雅普诺夫第二方法证明了平衡点的稳定性，可以看出水痘病毒的消失与否完全由基本再生数确定：如果基本再生数小于1，水痘病毒在人群中消失；然而如果基本再生数大于1，水痘病毒在人群中存在且形成地方病。

基金项目

河南科技大学大学生研究训练计划(SRTP)项目(项目编号：2019202)；河南科技大学青年学术带头人科研项目(项目编号：13490002)。