1. 引言
本文主要研究如下带有增值项的Cahn-Hilliard方程的初边值问题:
(1.1)
(1.2)
(1.3)
其中
是有界正则区域,n是边界上的单位外法向量,Δ是Laplace算子,f(s)和g(s)是非线性函数。当
时,即为标准的Cahn-Hilliard方程。Cahn-Hilliard方程描述了物理和化学中二元系统的相分离,它在1958年由J. W. Cahn和J. E. Hilliard [1] 首次以自由能的形式提出。后来,在动力学基础上,A. Novick-Cohen和L. A. Segel [2] 推导出了偏微分方程形式的Cahn-Hilliard方程。Cahn-Hilliard方程的L2的全局解和全局吸引子已经被广泛研究 [3] [4]。此外,在一定假设条件下,Cahn-Hilliard方程的
,
和
的全局吸引子的存在性已经在 [5] [6] [7] [8] 中给出。
本文关心的是广义的Cahn-Hilliard方程(1.1),即
的情形,称为带增值项的Cahn-Hilliard方程。它的研究目前已有不少的文献,如 [9] [10]。特别地,g可以是线性函数
,
。这种情况下的(1.1)就是Cahn-Hilliard-Oono方程,它说明了相分离过程中长距离(非局部)的相互作用,已有工作证明了它在有限维吸引子方面的渐近行为 [11]。g还可以是二次函数
,
。在这种情况下,(1.1)在生物学上有应用,更准确地说,在伤口愈合和肿瘤生长模型上有应用 [12]。
本文在如下更一般的假设条件下
(1.4)
(1.5)
研究方程(1.1)~(1.3)。
令
(1.6)
即
。
我们将用 [8] 的方法来研究在
空间上的带有一般增值项的Cahn-Hilliard方程的全局吸引子存在性问题。利用迭代思想,以及线性半群的正则性估计和全局吸引子的存在性定理来证明带有增值项的Cahn-Hilliard方程在
空间中有全局吸引子,它吸引
的任何有界子集。
我们给出一些记号 [8]:
(1.7)
2. 预备知识
设X和X1是Banach空间且
,考虑如下定义在X上的抽象非线性演化方程
(2.1)
其中,u(t)是未知函数,
是一个线性算子,
是一个非线性算子。
是由(2.1)生成的半群,(2.1)的解可以写成
。
定理2.1 [4]:设
是由(2.1)生成的半群。假设下面的条件成立:
1) S(t)有一个有界吸收集
,即对于任意有界集
,存在一个时间
,使得
,
;
2) S(t)是一致紧的;
则B的
-极限集
是(2.1)的一个全局吸引子。
如果(2.1)中的线性算子L是一个扇形算子,它生成解析半群
。不失一般性,我们假设L生成分数幂算子
和分数阶空间
如下:
其中,
是
的定义域。由半群理论,对于任意的
,都有
是紧包含。
引理2.1 [13]:
是一个扇形算子,它生成了解析半群
,则对于
有如下性质:
1)
是有界的,
,
,
2)
,
,
3)
,
有界,且
(2.2)
其中,某个
是常数。
4)
-范数可以定义为
(2.3)
由定理2.1有如下。
定理2.2 [8]:S(t)是由(2.1)生成的半群,
是(2.1)的解,设
是由L生成分数阶空间,若:
1) 对于某个
,有一个有界集
,对于任意的
,存在一个时间
,使得
,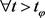 ;
;
2)
,对于任意的有界集
,有
,
,使得
,
,
;
则(2.1)有一个全局吸引子
。
3. 主要结果
本节中,我们将给出本文的主要结果。
设H和H1为(1.7)中定义的空间,线性算子
(3.1)
其中,f(u)同(1.4),g(u)同(1.5)。所以,(1.1)~(1.3)可以写成抽象形式(2.1)。
,L也是扇形算子,显
然
。
本文的主要结果是如下。
定理3.1:对初边值问题(1.1)~(1.3),假设f(u),g(u)分别由(1.4)和(1.5)给出;如果
,
;则对于任何的
,方程(1.1)~(1.3)在
中具有全局吸引子
,并且
在
-范数下吸引任何的
有界集。
证明:对于
时,任意的
以及
时,
,方程(1.1)对于任意的
有唯一强解
,
[8]。
所以,系统(1.1)~(1.3)的解
可以写成
(3.2)
接下来,就可以根据定理2.2 [8],用下面几个步骤在证明定理3.1。
i) 我们首先要证明,对于任意的有界集
,有一个常数
,使得系统(1.1)~(1.3)的解
对于任意的
和
是一致有界的。
让方程(1.1)乘
,再在Ω上积分有
(3.3)
进一步,
(3.4)
我们做如下假设:
(3.5)
(3.6)
(3.7)
特别地,当取
和
,
或
,
时,上面假设依然成立。
下面将假设(3.5)~(3.7)带入(3.3)~(3.4)有
(3.8)
此时,有
,用Gronwall引理,我们可得到
(3.9)
让方程(1.1)乘u,再在Ω上积分有
(3.10)
由f(u),g(u)的形式可得出:
(3.11)
(3.12)
特别地,当取
和
或
时,上面假设依然成立。
下面将假设(3.11)~(3.12)带入(3.10)有
由Gronwall引理,我们可得到
(3.13)
从而,
(3.14)
所以,
(3.15)
ii) 然后证明,对于任意的有界集
,有一个常数
,使得
(3.16)
实际上,从(2.3)和(3.2)可知
(3.17)
我们说
是有界的。
由
(当
时,显然成立;当
时,
)有
(3.18)
这就意味着
是有界的。
(3.19)
这就意味着
是有界的。
因此,由(2.2)和(3.15)可知
所以,(3.16)成立。
iii) 接下来证明,对于任意的有界集
,有一个常数
,使得
(3.20)
实际上,由分数阶空间的嵌入定理
可得
(3.21)
这意味着
(3.22)
是有界的。
因此,由(3.16)和(3.22)可得
(3.23)
而
(3.24)
这意味着
(3.25)
是有界的。
因此,由(3.16)和(3.25)可得
(3.26)
所以,我们可以得到
(3.27)
所以,(3.20)成立。
iv) 接下来再证明,对于任意的有界集
,有一个常数
,使得
(3.28)
实际上,由分数阶空间的嵌入定理
可得
(3.29)
这意味着
(3.30)
是有界的。
因此,由(3.20)和(3.30)可得
(3.31)
同理,
(3.32)
这意味着
(3.33)
是有界的。
因此,由(3.20)和(3.33)可得
(3.34)
所以,我们可以得到
(3.35)
所以,(3.28)成立。
v) 我们将证明,对于任意的有界集
,有一个常数
,使得
(3.36)
实际上,由分数阶空间的嵌入定理
可得
(3.37)
这意味着
(3.38)
是有界的。
因此,由(3.28)和(3.38)可得
(3.39)
同理,
(3.40)
这意味着
(3.41)
是有界的。
因此,由(3.28)和(3.41)可得
(3.42)
所以,我们可以得到
(3.43)
最后,不断重复步骤i)~iv),我们就可以得到(3.36)成立。