基于改进模糊智能算法的路径规划的研究

Research on Path Planning Based on Improved Fuzzy Intelligent Algorithm

摘要: 针对移动机器人面临环境的复杂性和不确定性，传统控制算法已经无法精确地避开障碍物，找到一条最优路径来完成相应的任务。针对这个问题，本文提出了一种改进的智能控制算法——参数自整定模糊逻辑控制算法，通过利用MATLAB编程，对模糊变量及模糊控制器进行设计，在随机的环境中对模糊控制器的相关参数进行自动校正，使其不受外界环境的影响，还可以精确地避开相应的障碍物，保证机器人能够准确地到达目标点，在此基础上可以得到一条最优路径。这种智能算法有效地解决了目前移动机器人所面临的主要问题，同时还可使控制系统保持较好的性能，实验结果表明该方法的优越性和可行性。

Abstract: In view of the complexity and uncertainty of the mobile robot’s environment, traditional control algorithms have been unable to accurately avoid obstacles and find an optimal path to complete the corresponding task. Aiming at this problem, this paper proposes an improved intelligent control algorithm—parameter self-tuning fuzzy logic control algorithm. By using MATLAB programming, the fuzzy variables and fuzzy controllers are designed. The parameters are automatically corrected so that they are not affected by the external environment, and the corresponding obstacles can be accurately avoided to ensure that the robot can accurately reach the target point. Based on this, an optimal path can be obtained. This intelligent algorithm effectively solves the main problems currently faced by mobile robots, and at the same time can keep the control system with good performance. Experimental results show the superiority and feasibility of the method.

1. 引言

随着现在科学技术的发展，智能化的机器人不仅给人民的生活带来了便利，也进一步促进科学技术的发展。机器人的研究则成了现代许多研究者研究的一个趋势，而路径规划是机器人研究的一个基础，也是关键因素 [1]。其主要任务是：当机器人在外部环境工作时，在由传统的控制算法对路径规划的研究转向为一些仿生智能的优化算法对最优路径的探讨。比如由传统的控制方法中的可视图法、人工势场法等 [2] 转为遗传算法、模糊逻辑控制法等 [3] [4]。可视图方法相对简单直观，比较快地求得最短路径，可视图方法相对简单直观，比较快地求得最短路径，但是它无法在动态的环境中求得相应的位置，缺少灵活性 [5] [6]。而相对于人工势场法来说：虽然结构相对来说比较简单，在轨迹控制方面应用比较广泛，但由于局部最优解的问题，容易产生死锁 [2] [7]。传统的遗传算法存在局部寻优精度不高，而且搜索时间较长，且容易存在局部最优的问题 [8]；传统的模糊逻辑控制算法虽然不依赖环境，计算量比较小，但仍然不能精确地找到路径规划中的最优路径 [9]。

在实际的工程中，不仅环境条件是复杂多变的，而且要求精确度非常高，综合以上算法及相应的因素，需要在模糊逻辑算法的基础上加以改进 [10] [11]。参数自整定模糊逻辑智能控制算法称为比例因子自整定模糊逻辑控制算法。这种控制算法是把仿生机器人中的感知和动作以及自身具有的强鲁棒性有机结合起来，避开了传统算法对移动机器人依赖环境强的缺点，对处理未知环境下的规划问题，具有很大的优势 [12]。模糊控制器是模糊控制智能算法的核心 [13]，因此模糊控制器的设计关系到模糊控制算法能否准确地对相应的路径规划产生精准的控制。

2. 改进型的模糊控制器的设计

2.1. 模糊控制器的输入输出变量

在仿生机器人运动规划路径的过程中，需要考虑机器人距障碍物的距离有多远，以便于机器人能够做出及时的调整。另外，如果遇到障碍物还要清晰的判断出在左边还是右边，这样能够及时的调整方向，所以基于此本文选取了距障碍物的距离和左右间的距离作为模糊控制器的输入 [14]。在输出的过程中首先考虑的是机器人行走的步长和避开障碍物转动的角度，要保证机器人行走的步长小于距障碍物之间的距离以及遇到障碍物转动的角度较小，而且最后还要能够回到原来的轨迹上。

2.2. 模糊化

本文中选取了两个输入变量分别是：机器人与障碍物之间的距离(Distance Of Barrier)和以及左右之间的距离(Left-Right)，也就是机器人的位置的参数并不能作为模糊控制器的输入，它们必须经过模糊化处理变成模糊控制器的输入变量 [15] [16]。这也是设计模糊控制系统的第一步。将Distance Of Barrier的论域设定为[0,10]，采用的是梯形隶属度函数，其模糊输入变量的语言为：{VS, S, M, B, VB}，而另一个输入变量Left-Right的论域设定为[−10,10]，其模糊语言变量为{RVB, RB, CE, LB, LVB}，而输出变量有机器人行走的步长(Scale Of Step)和机器人转动的角度(Scale Of Angle)，其论域分别为：[0,2]和[−2,2]，模糊语言变量：分别为{VS, S, M, B, VB}和{RVB, TRB, CE, TLB, TLVB}，其各字母的含义为(V: Very, S: Small, M: Middle, B: Big, R: Right, L: Left, CE: centre, T: Turn)，采用的是都是梯形隶属度函数，其输入变量Distance Of Barrier的隶属度如图1所示。

Figure 1. The membership function of Distance Of Barrier

图1. Distance Of Barrier的隶属度函数

2.3. 建立模糊规则

机器人的路径规划是保证能够避开障碍物而且尽量到达目标位置。机器人根据目标和障碍物的位置的不同而发生相应的变化，如果在机器人的左右侧都有障碍物时，则需要根据机器人的距离左右侧距离的大小判断该左转还是右转，如果是左侧大于右侧，则左转，反之依然。模糊控制器的核心是规则库，其模糊控制器的规则一般形式如下：

$\text{Rl:}{\text{IFx}}_{1}is{\text{A}}_{\text{1l}}{\text{andx}}_{\text{2}}{\text{isA}}_{\text{2l}}\cdots {\text{andx}}_{\text{i}}{\text{isA}}_{\text{il}}\cdots {\text{andx}}_{\text{n}}{\text{isA}}_{\text{nl}}$

${\text{THENyisB}}_{\text{l}}\left(\text{i}=1,2,3,\cdots ,\text{n};\text{l}=1,2,3,\cdots ,\text{m}\right)$ (1)

其中：模糊输入输出量分别为x_i，y；X，Y上的模糊子集分别为A_il，B_l。在模糊规则控制理论中，任何一条规则都有：A_1l × A_2l × … × A_nl→B_l 它是x × y = x₁ × x₂ …x_n × y的模糊关系，即

${\text{R}}_{\text{l}}\left(\text{x},\text{y}\right)={\text{R}}_{\text{l}}\left({\text{x}}_1,{\text{x}}_2,\cdots ,\text{y}\right)={\text{A}}_{\text{1l}}\times {\text{A}}_{\text{2l}}\times \cdots \times {\text{A}}_{\text{nl}}\times {\text{B}}_{\text{l}}$ (2)

其隶属度函数为：

$\begin{array}{c}{\text{u}}_{\text{Rl}}\left(\text{x,y}\right)={\text{u}}_{\text{Rl}}\left({\text{x}}_{\text{1}}{\text{,x}}_{\text{2}},\cdots ,\text{y}\right)\\ ={\text{u}}_{\text{A1l}}\left({\text{x}}_1\right)\times {\text{u}}_{\text{A2l}}\left({\text{x}}_2\right)\times \cdots \times {\text{u}}_{\text{Anl}}\left({\text{x}}_{\text{n}}\right)\times {\text{u}}_{\text{Bl}}\left(\text{y}\right)\end{array}$ (3)

本文中采用公式2的表达式，其模糊控制器的输入和输出都有两个，为了能够达到理想的效果，其控制规则也有两种情况，第一种是Distance Of Barrier和Scale Of Step，其目的就是保证机器人能够成功的避开障碍物，它们之间的规则是同步变化的，即当Distance Of Barrier取VS时，Scale Of Step也取VS。相对于机器人转动的角度要复杂一些，需要两个输入变量同时作用，其模糊控制器的规则如表1所示。

Table 1. Table of fuzzy control rules

表1. 模糊控制规则表

为了更形象直观的观察控制效果，可以根据模糊推理规则，可查看模糊控制器的输入和输出之间的三维关系图，如图2和图3所示。

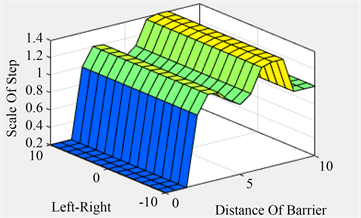
Figure 2. Simulation diagram of Distance Of Barrier, Left-Right and Scale Of Step

图2. Distance Of Barrier和Left-Right与Scale Of Step的仿真图

Figure 3. Simulation of Distance Of Barrier, Left-Right and Scale Of Angle

图3. Distance Of Barrier和Left-Right与Scale OfAngle的仿真图

2.4. 解模糊

模糊控制器输出的结果是对应的模糊变量，并不能够直接作为被控对象的控制量来控制机器人相应的参数，必须要把这些变量转化为机器人控制系统中的精确数值，这种转化的方法中最常用、最有效的只有三种，最大隶属度法、重心法和加权平均法 [17] [18]。在这三种方法中：只有重心法使模糊控制推理输出的曲线比最大隶属度函数要平滑的多，精确度更好，而且会随着模糊控制器输入参数发生变化，输出也会发生相应的变化。所以在本文采用的是重心法，它是根据模糊控制理论和数学的相关知识确定所围成面积的重心 [19]，即为模糊推理的输出值，即为：

$\text{U}=\frac{{\displaystyle \underset{i=1}{\overset{k}{\sum }}{y}_i{u}_B\ast \left(y_i\right)}}{{\displaystyle \underset{i=1}{\overset{k}{\sum }}{u}_B\ast \left(y_i\right)}}$ (4)

3. 改进模糊控制算法的仿真

在程序设计的过程中首先确定机器人开始目标位置相关参数，以及在路径线路上随机设置相应的圆形和直线型等形状的障碍物，机器人获得当前位置的目标点后，然后开始按照相应的路线进行行走 [20]，当机器人检测到前方有障碍物时，这需要采用上述的模糊控制智能算法，首先对输入量进行模糊化处理，然后经过模糊控制器推导出机器人的移动方向和移动距离的比例因子，以一定的探测角进行探测，最后根据与模糊控制器关联的探测距离进行探测前进。如果没有检测到相应的障碍物，则继续前行。具体的流程图如图4所示：

Figure 4. The block diagram of the program design of the improved fuzzy control algorithm

图4. 改进型模糊控制算法的程序设计框图

改进型的模糊控制算法的能够及时的调整自身的参数，使机器人保持较好的性能。图5是采用改进型模糊控制算法进行的仿真。

Figure 5. Simulation diagram of fuzzy control path planning

图5. 模糊控制的路径规划仿真图

实验结果显示，采用模糊控制智能算法，其路径规划不仅能够以较小的角度避开相应的障碍物，而且还能够以原来的路线到达相应的目标点。

为了说明模糊控制算法的应用更加的广泛，同时也是为了进一步说明改进型模糊控制智能算法的在路径规划问题上的优越性，本文做了一个基于模糊控制算法的智能小车的仿真仿真实验，仿真实验的结果如图6所示：

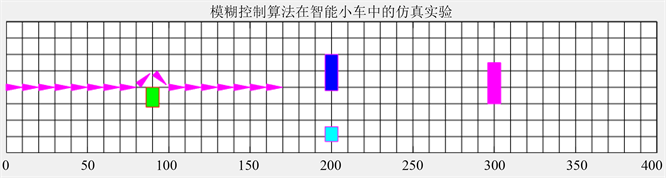(a)(b)

Figure 6. (a) Simulation experiment of fuzzy control algorithm in smart car; (b) Simulation experiment of fuzzy control algorithm in smart car

图6. (a) 模糊控制算法在智能小车中的仿真实验；(b) 模糊控制算法在智能小车中的仿真实验

仿真实验的结果表明：不但可以比较精确的判断障碍物的距左右之间的距离，能够自动的躲避相应的障碍物，还可以在避开障碍物之后还可以回到最初的轨道上来，沿着直线继续运行。

4. 结语

改进型的模糊智能控制算法在保证机器人不触碰障碍物的同时得到了一条最优路径。由仿真实验结果表明：这种算法能够有效地改善移动机器人的路径规划，在准确地避开障碍物的同时，到达相应的目标位置。使用这种算法可以表现出很好的一致性、连续性和稳定性。另外模糊逻辑控制算法也不需要考虑外界环境的复杂性，而且运算量比较小，具有一定的优越性。

基金项目

广西高校中青年教师基础能力提升项目(2019KY0874)，广西科技师范学院校级项目(GXKS2018YB013)。

参考文献