复杂交通节点的车流优化控制方案

Research on Optimal Traffic Flow Control Scheme for a Complex Traffic Node

摘要: 随着城市汽车保有量激增，交通系统负载过重，交通拥堵已成常态，设法缓解交通拥堵问题刻不容缓。本文研究复杂交通网络节点的车流量优化控制方法，旨在提升节点车流运行效率。首先，我们采集了诚毅学院附近的各个路口高峰时段的车流量数据；接着，根据各道之间车流实际变换情况，引入车辆变道的转换系数，利用差分方程基本理论，建立复杂交通节点的车流量动态模型；然后，利用采集的数据验证模型有效性和可靠性；最后，根据实际情形，给出了车流优化控制方案，并评测了方案的实际效果。

Abstract: With the rapid increase of urban car ownership and the overload of the transportation system, traffic congestion has become the norm. It is urgent to try to alleviate the problem of traffic congestion. This paper studies the optimal traffic flow scheme for a complex traffic node, aiming to improve the efficiency of the traffic flow at this node. Firstly, we collected the traffic flow data of each lane near Chengyi College during peak hours; secondly, according to the actual change of traffic flow between the lanes, we establish the dynamic model of traffic flow using the conversion coefficient of lane change and the basic theory of difference equations; thirdly, we verify the validity and reliability of the model by the collected data i; finally, according to the actual situation, we present the optimal control scheme of traffic flow, and evaluate the actual efficiency of the scheme.

1. 引言

1.1. 研究背景及意义

随着我国经济的飞速发展，人民生活水平不断提升，城市家庭步入家家有汽车的小康时代。近年来，城市汽车的保有量持续迅速增长，截至2019年，我国有超过66个城市的汽车保有量超百万辆，其中北京、成都、重庆、苏州、上海、郑州、深圳、西安、武汉、东莞、天津等城市的汽车保有量超300万，给城市交通系统造成巨大冲击，交通拥堵已成常态。优化交通网络系统，寻求解决或缓解交通拥堵问题的方案已成为城市交通管理部门的迫切需求。

汽车给城市居民提供交通便利的同时，也给城市道路资源带来前所未有的压力。即使政府大力提倡“公交出行、绿色出行”，在上下班高峰期，城市道路资源仍然极易达到饱和甚至超负荷的状态，研究如何充分利用城市道路资源，优化城市交通系统将是一个非常有意义的课题。城市交通系统相当于一个复杂网络，各个路口都是一个节点。各个节点相互关联，相互影响，略有微小变动，整个交通网络可能会发生巨大改变。王璐璐 [1] 认为交通事故、天气因素、不同节日时间点虽然都是影响交通拥堵的客观因素，但车流量增加到超过所处节点的最大容量是造成交通拥堵的最重要原因。

交通拥堵不仅使每个交通参与者造成时间的浪费，还会给城市带来更多的尾气排放，造成更大的环境污染问题，同时，会对整个社会经济带来极大的影响。《European Transport Policy and Sustainable Mobility》 [2] 中，David Banister研究发现，交通拥堵对城市GDP造成严重的损耗，通过对伦敦未来10年交通系统流量进行预测，预计交通拥堵将会对伦敦GDP的损耗值增加142%。因此，解决交通拥堵问题刻不容缓。

1.2. 研究的现状

城市车流量和城市道路资源之间的矛盾日益凸显，交通网络系统的问题日渐明显，学者对复杂交通网络系统的研究深度与广度不断提升。由于交通网络各个节点的车流量是不均衡变化的，具有随机意义的，对交通流量未来的预测具有重要的研究意义。卢官明 [3] 等人表示采用隐变量的方法，利用自适应建模的动态随机过程进行分析，引入具有相关性的双变量的信息系数，运用时间序列的属性加权法可以有效预测系统车流量未来的走势。赵倩芸 [4] 收集了交通流预测的各种算法，通过研究发现利用梯度提升回归树算法，可以有效处理交通流数据的异常值与缺失值，从而可以对系统车流量进行较好的预测。Shimizu H [5] 对复杂交通网络的控制系统进行分析，运用诱导与偏重式协同的方法，建立二级交通系统控制路网模型，来缓解车流量过多的问题。赵铁柱 [6] 分析了复杂网络的结构特性，利用FN算法进行分类讨论，最后指出，可以利用网络连通可靠性指标对交通系统进行有效解析。吕文红 [7] 从无标度特性、可靠性等角度进行分析挖掘，构建动态网络有向模型，对道路拥堵进行成因分析，并给出了优化依据。刘爱佳 [8] 运用矢量模型建立交通线路网络和站点网络模型，运用聚焦系数，拓扑参数，对交通网络的流通量开展预测分析。冯宁 [9] 利用了时空注意力机制对未来交通流进行分析预测。

对于交通系统优化的方案，学者们更是提出各自独特见解。有的运用离散模型来优化道路的交通问题，有的建立多目标优化模型，有的运用SCATS系统来控制路口车流量。王力 [10] 通过对交通网络进行节点的分析，以高峰时期的路口车流量和节点系数作为评价指标，利用聚类分析获得网络路口的相关特性。陈晓明 [11] 通过指标验证，对交通网络的节点与位置进行优化。

1.3. 本文的思路与目的

汽车排放的尾气是城市环境的重要污染源，交通拥堵显然会导致汽车尾气排放量的增加，给城市环境造成更严重的污染。与此同时，交通拥堵会显著提升城市居民出行的经济成本和时间成本。目前，厦门市的日均车流量达到了88.13万辆，四桥一隧在上下班高峰期拥堵成为常态，有数据显示，厦门市最拥堵路段的拥堵指数最高达到2.18。本文以集美区诚毅学院门口的交通复杂路口为例，我们实地采集了拥堵时段各个车道的车流量数据，对该复杂交通网络节点建立车流量分析动态模型，旨在通过建立车道内车流量的优化控制方案，使该节点获得更大的通行能力，从而尽可能缓解该节点的交通拥堵问题。

本文主要研究复杂交通节点因汽车变道、节点车流量的变化导致的通行能力减弱问题。事实上，车辆变道频率会对节点的各个车道的通行能力造成极大影响。当节点内各个车道的车流处于稀疏状态时，车辆变道进入或离开车道不会对车道内正常行驶的车辆造成任何影响；当各个车道的车流处于即将饱和状态时，若进入节点车道的车流量仍然不断增加，此时如果有车辆变道现象，则可对车道内正常行驶的车辆造成一定影响；当各个车道的车流达到饱和状态时，车辆变道现象将对车道内正常行驶的车辆造成明显影响，直至出现明显拥堵现象。因此，本文对车道之间的转换关系、流入各车道的车流量数据和驶出该车道的车流量数据进行研究，建立车流量模型。最后根据实际状况给出相应的车流优化控制方案。

2. 复杂交通节点路况分析

2.1. 交通节点路况描述

本文采集了诚毅学院路口的复杂交通网络节点的工作日上下班高峰期、周末及节假日拥堵时段的车流通行数据，建立描述节点内各个车道的车流量动态变化的数学模型，分析造成节点车辆通行能力降低的成因，从而有针对性的提出节点车流量优化控制策略，以期达到提升节点通行能力的目的。

本文研究的复杂交通网络节点简化后的示意图见图1。在拥堵时段内，车辆从各向涌入该节点，各个车道的车流量迅速增加，车道很快接近饱和状态，车辆通行速度明显变慢，通行时间增长。此时，调头区车辆的涌入，各车道的通行能力极易被打破，车道间发生车辆变道的可能性增加，从而进一步降低了各个车道车辆的通行速度，加剧了该节点的交通拥堵。

本文作者分别在该节点的观察点A(调头区下方)和观察点B进行数据采集，两个观察点距离500米。本文所提及的某时刻某车道的车流量 $Q\left(t\right)$ 就是指在观察时刻t，在两个观察点之间，该车道内车辆的存有数量。当 $Q\left(t\right)=0$ 时，表示该时刻该车道内无车辆，交通状况良好； $Q\left(t\right)$ 的值越大，表明该时刻该车道内的车辆越多，交通越拥堵，车辆通行速度越慢。

2.2. 节点模型简化及关键分析

诚毅路口的复杂网络简化图见图1。

把五个车道简称为A、B、C、D、E。各个车道的动态变化的车流量数据都受到流入、流出该车道的车流量的影响，以及相邻车道之间车辆互相转换的影响。除此之外，A道还受到了对向掉头的车流量的影响。

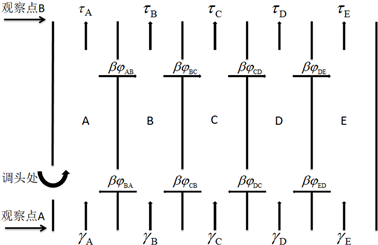
Figure 1. Simplified map of Chengyi intersection

图1. 诚毅路口简化图

每个车道自身进入的车流量是不稳定的，随机的。对于不同时期流入的车流量也会产生差异，因此，本文通过收集了拥堵时间的车道车流量流入数据，进行研究分析。每个车道自身流出的车流量也是变化的，本文在拥堵时刻，根据图1观察点B的调查表明，在诚毅路口的流出的车流量与前方的红绿灯时间长短有关。在单位时间内，辅道各车道一般流出的车流量约18辆，主道各车道流出车流量约19辆。考虑各道之间都有基础的车流量。联系实际来观察，各道基础车流量也与所处时间、日期有关联，考虑各个时期的基础车流量是不同的。

本文先研究辅道与主道之间的车道变换以及车道车流量的变化规律。再对A、B、C、D、E五道进行细致的研究分析。

3. 模型的建立与求解

3.1. 模型的假设

1) 假设车道之间的转换系数 $\beta$ 只与转换车道之间的实际通行能力有关。

2) 假设观察路段不发生交通事故。

3.2. 符号说明

为准确表达本文模型的数学意义，特引入本文常用的数学符号，其含义说明如下：

3.3. 部分概念说明

1) 每个车道都有自身的实际通行能力，本文对实际通行能力 ${\phi }_i\left(t\right)$ 的解析是，观察时刻内的车道存有的车流量的值与流出该车道的车流量的值之间的差值。在t时刻时，车道中的车流量为，流出的车流量为 ${\tau }_i\left(t\right)$，车道的实际通行能力 ${\phi }_i\left(t\right)$ 为两者的差值，即 ${\phi }_i\left(t\right)={\tau }_i\left(t\right)-\left(Q_i\left(t-1\right)+{\gamma }_i\left(t\right)\right)$。

2) 各道之间的转换变道存在一个转换系数 ${\beta }_{ij}$。当转换车道速度快时，其通行能力较好，驾驶员可以考虑变道。本文通过比较通行能力来衡量转换系数。当在A道通行能力优于B道时，有 ${\phi }_A>{\phi }_B$，即假定 ${\beta }_{AB}=1-{\phi }_B/{\phi }_A$，则此时A道的车速快于B道，这时B道的驾驶员考虑向A道变道；当在A道通行能力差于B道时，有 ${\phi }_A<{\phi }_B$，即假定 ${\beta }_{AB}=1-{\phi }_A/{\phi }_B$，这时A道的驾驶员考虑向B道变道。

3) 各个车道的流出车流量 ${\tau }_i\left(t\right)$。当此刻车道A的车流量少于18辆时，即 $Q_A\left(t-1\right)+{\gamma }_A\left(t\right)<18$ 时， ${\tau }_A\left(t\right)=Q_A\left(t-1\right)+{\gamma }_A\left(t\right)$ ；当此刻车道A的车流量不小于18辆时，即 $Q_A\left(t-1\right)+{\gamma }_A\left(t\right)\ge 18$ 时， ${\tau }_A\left(t\right)=18$。B道同理。当此刻车道C的车流量少于19辆时， ${\tau }_C\left(t\right)=Q_C\left(t-1\right)+{\gamma }_C\left(t\right)$ ；当此刻车道C的车流量不小于19辆时， ${\tau }_C\left(t\right)=19$。D道、E道同理。

3.4. 主道与辅道模型建立

分析主道与辅道之间车流相互交互作用下，两道车道的车流量变化。主道与辅道的车流量变换过程见图2。

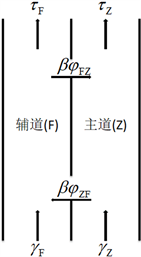
Figure 2. Schematic of the change of traffic flow between the auxiliary road and the main road

图2. 辅道与主道之间车流变化示意图

t时刻，辅道车道的车流量由上一刻的车流量 $Q_F\left(t-1\right)$，在t时刻流入辅道车道的车流量 ${\gamma }_F\left(t\right)$，流出观察路段辅道车道的车流量 ${\tau }_F\left(t-1\right)$，以及A车道与B车道之间的转换车辆 ${\beta }_{FZ}{\phi }_{FZ}\left(t-1\right)$ 构成。则辅道车道在t时刻的车流量数量关系式如下：

$Q_F\left(t\right)=Q_F\left(t-1\right)+{\gamma }_F\left(t\right)-{\tau }_F\left(t-1\right)+{\beta }_{FZ}\ast {\phi }_{FZ}\left(t-1\right)$ (1)

其中， ${\beta }_{ij}={\beta }_{ij}\left(t-1\right),{\phi }_{ij}\left(t-1\right)={\phi }_i\left(t-1\right)-{\phi }_j\left(t-1\right)$。

对于主道车道在t时刻的车流量数量关系式如下：

$Q_Z\left(t\right)=Q_Z\left(t-1\right)+{\gamma }_Z\left(t\right)-{\tau }_Z\left(t-1\right)+{\beta }_{FZ}\ast {\phi }_{ZF}\left(t-1\right)$ (2)

则辅道车流量与主道车流量函数模型的关系式所下：

$\{\begin{array}{l}{Q}_F\left(t\right)=Q_F\left(t-1\right)+{\gamma }_F\left(t\right)-{\tau }_F\left(t-1\right)+{\beta }_{FZ}\ast {\phi }_{FZ}\left(t-1\right)\\ Q_Z\left(t\right)=Q_Z\left(t-1\right)+{\gamma }_Z\left(t\right)-{\tau }_Z\left(t-1\right)+{\beta }_{FZ}\ast {\phi }_{ZF}\left(t-1\right)\end{array}$ (3)

进入车道的车流量数据与时间存在一个函数关系，在拥堵时刻车流量会逐渐增多，随着时间的变化，车流量会开始慢慢减少。通过调查研究，进行分析处理，对于辅道流入的车流量变化见图3。

Figure 3. Schematic diagram of inbound vehicle traffic data

图3. 辅道流入车流量数据示意图

观察数据，发现在1~6时刻，即在观察的12分钟内，流入辅道的车流量差值不大，所以在1~6时刻的 ${\gamma }_F$ 取均值，此时 ${\gamma }_F=44$。在7~17时刻，即观察的20分钟内，流入辅道的车流量可以用一个二次函数表示， ${\gamma }_F=-0.038x^2-0.81x+43$。在18~30时刻，即观察的24分钟内，流入辅道的车流量之间的差值较平均，将 ${\gamma }_F$ 取均值，即 ${\gamma }_F=19$。得到一个关于 ${\gamma }_F$ 的函数关系式：

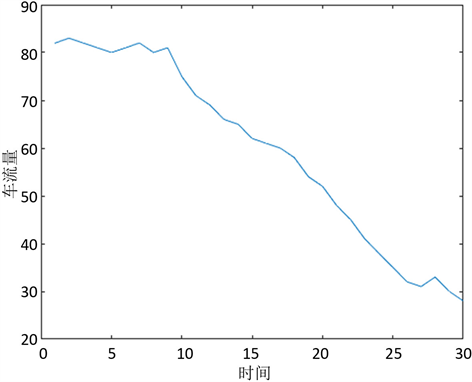
Figure 4. Schematic diagram of inbound traffic data on the main road

图4. 主道流入车流量数据示意图

${\gamma }_F=\{\begin{array}{c}\begin{array}{ll}44\hfill & 1\le t\le 6\hfill \\ -0.038x^2-0.81x+43\hfill & 7\le t\le 17\hfill \\ 19\hfill & 18\le t\le 30\hfill \end{array}\end{array}$ (4)

对于主道流入的车流量变化见图4。

观察数据，发现在1~8时刻，即观察的16分钟内，流入辅道的车流量之间的差值较小，所以在1~8时刻的 ${\gamma }_Z$ 取均值，此时 ${\gamma }_Z=82$。在9~24时刻，即观察的30分钟内，流入辅道的车流量可以用一个二次函数表示， ${\gamma }_Z=-0.065x^2-0.38x+82$。在25~30时刻，即观察的10分钟内，流入辅道的车流量之间的差值较平均，将 ${\gamma }_Z$ 取均值，即 ${\gamma }_Z=31$。得到一个关于 ${\gamma }_Z$ 的函数关系式：

${\gamma }_Z=\{\begin{array}{c}\begin{array}{ll}82\hfill & 1\le t\le 8\hfill \\ -0.065x^2-0.38x+82\hfill & 9\le t\le 24\hfill \\ 31\hfill & 25\le t\le 30\hfill \end{array}\end{array}$ (5)

3.5. 主道与辅道模型的求解与验证

将 $Q_F\left(0\right)=27$， $Q_Z\left(0\right)=40$， ${\gamma }_Z$ (式(4))、 ${\gamma }_F$ (式(5))代入式(3)中，得到的数据结果见表1。

Table 1. True value, fitted value and relative error of main road and auxiliary road traffic

表1. 主道辅道车流量真实值、拟合值及相对误差

通过表1可以观察到，拟合的车流量数据与真实值之间的相对误差较小，说明拟合程度较好。在时刻到 $t=13$ 时刻时，车道的车流量逐渐增多，车道的实际通行能力减弱，车道拥堵状态逐渐增强。在 $t=14$ 时刻以后，车道的车流量在缓慢减少，车道实际通行能力逐渐增加，车道的拥堵状态逐渐缓和。从表可以观察到在 $t=13$ 时车道车流量最多，此时最为拥堵。

3.6. 各道车流量模型建立

对各个车道进行分析，五个车道的车流变化过程见图1。

由于A车道相较于其它四道，都受到了调头车辆 $d\left(t\right)$ 的影响，因此对于任意t时刻的各道的车流量方程如下：

$\begin{array}{l}{Q}_A\left(t\right)=Q_A\left(t-1\right)+d\left(t\right)+{\gamma }_A\left(t\right)-{\tau }_A\left(t-1\right)+{\beta }_{AB}\ast {\phi }_{AB}\left(t-1\right)\\ Q_B\left(t\right)=Q_B\left(t-1\right)+{\gamma }_B\left(t\right)-{\tau }_B\left(t-1\right)+{\beta }_{AB}\ast {\phi }_{BA}\left(t-1\right)+{\beta }_{BC}\ast {\phi }_{BC}\left(t-1\right)\\ Q_C\left(t\right)=Q_C\left(t-1\right)+{\gamma }_C\left(t\right)-{\tau }_C\left(t-1\right)+{\beta }_{BC}\ast {\phi }_{CB}\left(t-1\right)+{\beta }_{CD}\ast {\phi }_{CD}\left(t-1\right)\\ Q_D\left(t\right)=Q_D\left(t-1\right)+{\gamma }_D\left(t\right)-{\tau }_D\left(t-1\right)+{\beta }_{CD}\ast {\phi }_{DC}\left(t-1\right)+{\beta }_{DE}\ast {\phi }_{DE}\left(t-1\right)\\ Q_E\left(t\right)=Q_E\left(t-1\right)+{\gamma }_E\left(t\right)-{\tau }_E\left(t-1\right)+{\beta }_{DE}\ast {\phi }_{ED}\left(t-1\right)\end{array}$ (6)

对辅道车道，A车道与B车道流入的车流量的变化进行分析，变化过程见图5。

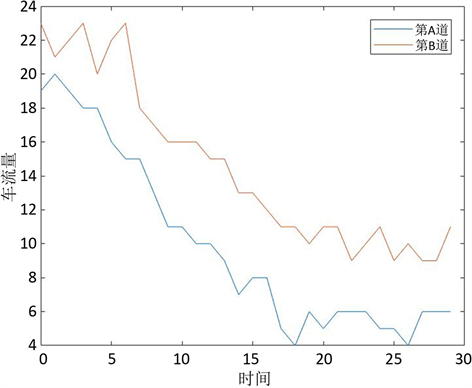
Figure 5. Schematic diagram of the changes in the inflow traffic of lanes A and B

图5. A车道、B车道流入车流量变化示意图

观察数据，得到一个关于 ${\gamma }_A$ 的函数关系式：

${\gamma }_A=\{\begin{array}{c}\begin{array}{ll}19\hfill & 1\le t\le 5\hfill \\ 0.05x^2-2x+26\hfill & 6\le t\le 17\hfill \\ 6\hfill & 18\le t\le 30\hfill \end{array}\end{array}$ (7)

对B车道的流入车流量数据进行分析，即得到一个关于 ${\gamma }_B$ 的函数如下所示：

${\gamma }_B=\{\begin{array}{c}\begin{array}{ll}22\hfill & 1\le t\le 7\hfill \\ 0.023x^2-0.044x+19\hfill & 8\le t\le 17\hfill \\ 11\hfill & 18\le t\le 30\hfill \end{array}\end{array}$ (8)

对于主道的流入车流量，C车道与D车道、E车道流入的车流量的变化进行分析，变化过程见图6。

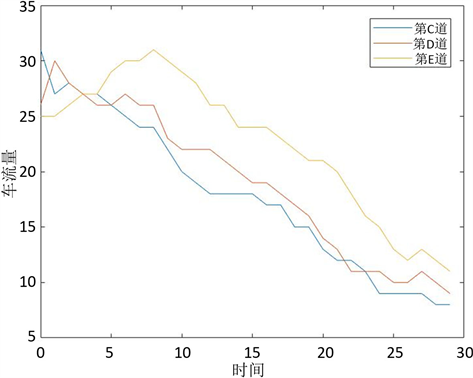
Figure 6. Schematic diagram of the changes in the inflow traffic of lanes C, D and E

图6. C车道、D车道、E车道流入车流量变化示意图

观察数据，对C车道流入车流量进行分析，得到的关于 ${\gamma }_C$ 的函数如下所示：

${\gamma }_C=\{\begin{array}{c}\begin{array}{ll}27\hfill & 1\le t\le 9\hfill \\ -0.017x^2-0.13x+24\hfill & 10\le t\le 24\hfill \\ 9\hfill & 25\le t\le 30\hfill \end{array}\end{array}$ (9)

对D车道的流入车流量数据进行分析，即得到一个关于 ${\gamma }_D$ 的函数如下所示：

${\gamma }_D=\{\begin{array}{c}\begin{array}{ll}27\hfill & 1\le t\le 9\hfill \\ -0.053x^2+0.88x+19\hfill & 10\le t\le 23\hfill \\ 11\hfill & 24\le t\le 30\hfill \end{array}\end{array}$ (10)

对E车道的流入车流量数据进行分析，即得到一个关于 ${\gamma }_E$ 的函数如下所示：

${\gamma }_E=\{\begin{array}{l}291\le t\le 12\\ -0.051x^2+1.1x+2113\le t\le 25\\ 1326\le t\le 30\end{array}$ (11)

3.7. 各道车流量模型的求解

将 $Q_A\left(0\right)=13$， $Q_B\left(0\right)=14$， $Q_C\left(0\right)=14$， $Q_D\left(0\right)=13$， $Q_E\left(0\right)=13$， ${\gamma }_A$ 、 ${\gamma }_B$ 、 ${\gamma }_C$ 、 ${\gamma }_D$ 、 ${\gamma }_E$，以及收集的调头车辆 $d\left(t\right)$ 代入式(6)中，得到的拟合数据结果见表2。

Table 2. Fitting data of traffic flow in each lane on weekdays

表2. 工作日各车道车流量拟合数据

通过表2数据可以观察，A车道在 $t=23$ 时，拥堵了46分钟后，车道交通状态从拥堵转换为良好。B车道在 $t=21$ 时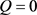，，此时车道交通状态良好。C车道，D车道，E车道，分别在 $t=25$ 时， $t=30$ 时， $t=26$ 时，交通状态良好。在观察的路段中，经过了一个小时的拥堵，车道的交通状态由拥堵转变为流畅的状态。要改善复杂交通节点的交通状态，减少其拥堵的时间，就是要对各道车流量进行控制优化，尽可能的减少道路拥堵的时间。

4. 车流量优化控制

4.1. 影响各道车流量变化的因素

用上述方法对节假日和周末的各道车流量数据进行分析。

将 $Q_A\left(0\right)=22$， $Q_B\left(0\right)=28$， $Q_C\left(0\right)=34$， $Q_D\left(0\right)=30$， $Q_E\left(0\right)=29$，收集得到的周末各道车流量离散数据 ${\gamma }_i$，以及收集的调头车辆 $d\left(t\right)$ 代入式子(6)中，得到周末的各道车流量部分数据结果见表3。

Table 3. Week-end traffic flow fitting data

表3. 周末各车道车流量拟合数据

通过表3可以观察到，周末日拥堵时间到 $t=39$ 的时候，拥堵了78分钟。

将 $Q_A\left(0\right)=25$， $Q_B\left(0\right)=29$， $Q_C\left(0\right)=37$， $Q_D\left(0\right)=33$， $Q_E\left(0\right)=33$，收集得到的节假日各道车流量离散数据 ${\gamma }_i$，以及收集的调头车辆 $d\left(t\right)$ 代入式子(6)中，得到节假日的各道车流量部分数据结果见表4。

Table 4. Fitting data of traffic flow in each lane on holidays

表4. 节假日各车道车流量拟合数据

节假日拥堵时间达到了104分钟。可以发现，各个日期不同，各道拥堵的时间不同，各道车流量变化也不同。因此影响各道车流量变化的因素与日期有关。通过观察模型上的变量发现，转换系数由于与流入车流量 ${\gamma }_i\left(t\right)$ 和流入车流量 ${\tau }_i\left(t\right)$ 有关，由于此刻流出车流量是一个稳定的值，因此，引起车流量变化的是，不同时期各道流入车流量的数据。周末，节假日流入各道的车流量会增多，拥堵的时间会增长。

本文还对天气因素进行观察，对雨天时各道车流量的数据变化进行研究，将 $Q_A\left(0\right)=20$， $Q_B\left(0\right)=26$， $Q_C\left(0\right)=32$， $Q_D\left(0\right)=28$， $Q_E\left(0\right)=27$， ${\tau }_A\left(0\right)=16$， ${\tau }_B\left(0\right)=16$， ${\tau }_C\left(0\right)=17$， ${\tau }_D\left(0\right)=17$， ${\tau }_E\left(0\right)=17$，收集的节假日各道车流量离散数据 ${\gamma }_i$，以及收集的调头车辆 $d\left(t\right)$ 代入式子(6)中，得到雨天时刻的各道车流量部分数据结果见表5。

Table 5. Fitting data of traffic flow in each lane on rainy days

表5. 雨天各车道车流量拟合数据

从表中可以发现，雨天时，拥堵时间为98分钟。可以发现天气也是引起各道车流量变化的因素。通过观察模型上的变量，总结出，天气原因主要是影响了流入车流量 ${\gamma }_i\left(t\right)$ 和流入车流量 ${\tau }_i\left(t\right)$，导致拥堵时间延长。

影响各道车流量变化的因素，都是通过影响转换系数 ${\beta }_{ij}$，流入车流量 ${\gamma }_i\left(t\right)$ 和流入车流量 ${\tau }_i\left(t\right)$，因此控制各道车流量就是要对流入、流出的车流量进行控制。

4.2. 车流量优化方案

要减缓复杂交通节点的拥堵时间，即要对各道的车流量进行控制优化。对各道车流量进行控制，来增加各道的实际通行能力，降低各道的拥堵程度。

首先，通过提高绿信比来，减缓拥堵的时间。考虑到，提升流出的车辆可以缓解交通拥堵，对各个车道前方的红绿灯时间进行调整。本文将绿信比由1/2提升到7/12，得到的各道车流量的部分数据结果见表6。

Table 6. Fitting data of traffic volume in each lane for changing the green letter ratio

表6. 更改绿信比的各车道车流量拟合数据

通过对比上述数据，发现提高绿信比，各道的车流量会有所减缓，与3.7中的数据相比，拥堵时间减少了20分钟。因此，适当提高绿信比，可以保证在观察路段内，各道存有的车流量减少，降低拥堵时间。

其次，适当控制流入车流量，可以减缓各道车流量数据，降低拥堵时长。控制流入各道的车流量为原来的0.9，则得到的各道车流量部分数据结果见表7。

Table 7. Fit traffic data for each lane to control incoming traffic

表7. 控制流入车流量的各车道车流量拟合数据

通过对比3.7中的数据，适当减缓各道流入的车流量可以减少各道内车流量数据，降低拥堵时间，即拥堵减少了22分钟。

控制各道流入车流量的实际方案有：实行单双号限行，来减缓每天的流入车流量。控制上下班分流时间，来对流入车流量较大的时间段进行缓和，控制拥堵时间的车流量。对道路进行扩容增道，也可以适当缓解交通拥堵。

最后，可以控制转换的车辆，来缓解交通拥堵。限制转换时的规则，比如，各道车流量过大，速度十分缓慢时，不允许变道或是延长实线的距离。

5. 总结

交通拥堵日益加重，解决复杂交通系统的交通状况，就是要改变其通行能力，增大通行能力，控制车流量，来减缓交通拥堵的问题。

本文以诚毅学院路口的拥堵路段为例，研究复杂交通节点的车流量变化趋势，以及对车流量的优化控制方案。本文通过运用各道之间的转换系数，实际通行能力，及各道流入流出的函数，来构建车流量模型。建立主道与辅道的车流量模型，并拟合数据，求出各道的车流量相对误差，进行验证，误差较小，拟合较好。接着对各道的车流量进行分析，考虑各道车流量在各个时刻变化的数据，来计算其拥堵的时间。其次还研究了不同日期，以及下雨天的因素，对各道存有车流量的影响，得出影响各道车流量数据变化，以及拥堵时间发生变化的是各道流入、流出的车流量，以及转换的车辆。最后提出对各道车流量进行优化控制，就是对流入及流出车流量、转换车辆进行控制，增强各道的实际通行能力，来减缓交通拥堵的时间。

本文主要以实际出发，研究拥堵时段的车流量数据，进行模型建立，提出实际的意见进行控制优化车流量。交通拥堵问题在各个城市已经很常见，拥堵对社会、个人造成的损失较大，缓解交通拥堵问题刻不容缓。解决交通拥堵问题，不仅可以节省时间，更可以减少GDP的损失。本文还存在些许不足，对模型建构考虑的因素不够具体，今后还可以继续完善。

基金项目

福建省中青年教师教育科研项目(项目编号：JAT160350)。

参考文献