1. 引言
上海原油期货是目前中国第一个也是唯一一个原油期货,同时也是中国期货业首个对外开放的品种。上海原油期货正式挂牌交易标志着中国期货市场国际化扬风起航,意味着人民币国际化迈出了重要一步,也意味着中国正式加入亚太原油定价权竞争。因此,本文选择上海原油期货作为研究对象。近年来国际油价波动剧烈,中国石油产业链相关企业面临较大的风险敞口,经营发展的不确定性大大增加。对上海原油期货价格波动影响因素的研究,将有利于为国内涉油企业提供有效的风险管理工具,有利于为产业链企业提供价格参考,有利于形成金融市场全面开放的新格局。
2. 文献综述
已有文献对原油期货价格波动的研究主要是从两个方面展开讨论,一是影响原油期货价格变动的有关因素,二是其他金融市场对原油期货价格波动的影响关系。
在研究原油期货价格影响因素的问题上,Hammoudeh和Li [1] 以亚洲金融危机为视角,运用向量误差修正模型,研究了美国和国际原油价格的影响因素。结果表明,因果关系在危机前后发生了改变。张珣等 [2] 着重研究石油期货价格波动影响因素中的突发事件,分析了三次突发事件,包括海湾战争、伊朗革命和伊拉克战争,证明突发事件对石油期货价格的波动影响显著。采用的方法有结构性断点检验和常收益事件分析模型。蒋瑛 [3] 着重研究石油期货价格波动影响因素中的投机行为,证明投机行为对石油期货价格的波动影响显著。采用的方法有误差修正模型、向量自回归和格兰杰因果关系检验。部慧等 [4] 在考虑投机活动的同时,还考虑了库存信息对市场预期的冲击。Lu等 [5] 运用Hong检验和DCC-MGARCH Hong检验,研究国际一些重大事件对原油期现货之间溢出效应的影响,探讨时变性的因果关系。李智等 [6] 选取三个内生变量和四个外生变量,涵盖了期货市场和石油供求相关影响因素,通过MSVAR模型对国际原油期货价格进行分析。表明西方国家的石油需求变化依然是决定石油期货价格变动的主要因素。马郑玮等 [7] 研究影响原油期货价格的因素包括原油现货价格、原油期货持仓量、美元汇率、原油库存、原油供需。
在研究其他金融市场对原油期货价格波动的影响问题上,Bekiros和Diks [8] 探讨了西德克萨斯原油的期货和现货和期货之间的关系,主要从非线性的因果关系入手。李聂 [9] 以中外石油期货合约的日收益率为视角,研究世界石油期货价格的波动性与合约到期日之间的关系,证明了世界石油期货收益率的到期日效应。甘欢欢和焦建玲 [10] 以纽约商品交易所的原油期货为例,运用GARCH类模型实证研究原油价格的收益和波动的关系,结果表明原油期货价格波动存在着杠杆效应及周日历效应。胡淑兰 [11] 通过GARCH模型和Markov机制转移模型,研究了三十年期间的世界原油期货价格波动结构转变特征。李丽红 [12] 以西得克萨斯中质原油期货价格与大庆原油价格关系为例,进行实证分析,结果表明,国际原油期货与国内原油现货价格的周期性互为联动的趋势越来越明显。刘映琳等 [13] 使用相关性结构断点和VaR分位数回归模型研究国际原油价格波动对中国商品期货的影响,结果表明我国商品期货与国际原油价格之间的相关性呈现某种“周期性”,周期持续期大约为七年。
3. 主成分分析法理论基础
在分析处理实际问题的过程中,有的问题是多变量(多指标)的。如果变量过多,会增加问题的复杂性。同时,在实际问题中,变量之间也可能存在一定的相关性,因此,多变量中可能存在信息的重叠。直接利用它们进行分析,不但模型复杂,还会因为变量间存在多重共线性而引起较大的误差。因此可以通过克服相关性、重叠性,用较少的新变量来代替原来较多的变量,而这种代替可以反映原来多个变量的大部分信息。这实际上是一种“降维”的思想,所以主成分分析可以对数据进行降维。
3.1. 主成分分析法模型
主成分分析的基本思想就是通过少数几个主分量来解释多个变量间的内部结构。即从原始变量中导出少数几个主分量(降低维数),同时使它们尽可能多地保留原始变量的信息,且彼此间互不相关。
主成分分析的数学模型公式如下:
(1)
主成分模型通过寻找原指标的线性组合Fi,来确定主成分的个数。而X的系数a即为特征向量。同时方程需满足下列条件:
1)
。
2) 主成分F之间互不相关。
。
3) 且方差依次递减。
。
3.2. 主成分分析模型推导
在了解主成分模型的实质含义之前,需要做线性代数相关方面的准备。我们知道若A是p阶实对称阵,则一定可以找到正交阵U,使
(2)
其中
是A的特征根。如果该矩阵的特征根所对应的单位特征向量为U,
(3)
则实对称阵A属于不同特征根所对应的特征向量是正交的,即有
。
主成分模型寻找的一组新的变量
,要求充分地反映原来变量
的信息,而且相互独立。对于
有
(4)
(5)
这样,根据主成分携带信息最大(或者损失信息最小)的原则,我们所要解决的问题就转化为,在新的变量
相互独立的条件下,求
使得
,达到最大。
首先应该注意到,使得
达到最大的线性组合,显然用常数乘以
后,
也随着增大,为了消除这种不确定性,不妨假设
满足
或者
。那么,问题可以更加明确。
第一主成分为,满足
,使得
达到最大的
。
第二主成分为,满足
,且
,使得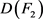 达到最大的
。
达到最大的
。
一般情况下,第k个主成分满足
,且
,使得
达到最大的
。
3.3. 主成分分析法步骤
第一步:对原来的p个指标进行标准化,以消除变量在水平和量纲上的影响。
第二步:计算原始变量的协方差或相关系数矩阵R,或进行KMO和Bartlett球形度检验,判断是否适合做主成分分析。
第三步:计算协方差矩阵或相关系数矩阵R的特征值λ (主成份的方差),并按从大到小的顺序排列。
第四步:计算特征值对应的特征向量,即为主成分相应的系数。
第五步:计算出主成分得分,进而可以把各个主成分看作新的变量代替原始变量,从而达到降维的目的。
4. 实证分析
期货价格对国际大宗商品定价体系有着至关重要的影响。原油的期现货协同发展,对于期货的价格发现功能起到了关键性的作用。上海原油期货遵循“国际平台、净价交易、保税交割、人民币计价”的宗旨,其服务实体经济的功能也因此而初步显现。和布伦特原油期货、WTI原油期货不同,上海原油期货价格本质上是一个到岸价格。因此,影响上海原油价格波动的因素也会有所不同。
上海原油期货的意义和作用之一就是为了反映中国原油市场的供需结构变化,从而得到一个更加贴合市场的价格,因此市场在交投时产生的价格一定会更多参考目前中国原油市场的基本面情况。
4.1. 影响因子的选取
原油期货虽然是依托原油价格的衍生金融工具,但是与原油息息相关。其影响因素不仅涉及到原油范畴,也包括原油期货本身的特性。一方面,对于原油,其作为国家生存和发展不可或缺的战略资源,被市场赋予双重属性,即本身具有的商品属性和衍生的金融属性。原油不仅在全球贸易中占据相当重要的地位,而且还与世界各国的政治、金融、经济等方面密切相关。另一方面,对于期货,上海原油期货价格的影响因素和其他市场的原油期货一样,涉及基本面因素、地缘政治因素、宏观因素、资金因素等。因此,综合各方面的考虑,本文的研究角度,主要是以原油期货的商品属性和金融属性为主,地缘政治因素为辅,来探讨上海原油期货价格的影响因素。
4.1.1. 商品属性
所谓的商品属性与原油期货产品的微观影响因素相关,其中最重要的就是原油的供需关系。原油作为一种商品,对全球经济影响巨大。原油不仅具有一般的商品属性,还具有战略物资的属性,所以其供应和价格在很大程度上会受到政治局势和势力的影响。21世纪以来,随着经济全球化、生产国际化的发展,争夺石油资源和控制石油市场,已成为各个国家石油市场变化激烈和油价频繁波动的重要原因。
上海原油期货反映中国沿海原油市场供需,一方面长期以来与国际油价保持较好联动,另一方面在本地区突发事件发生时,能够更直接、更快速地有所反应。尤其是面对突发事件时,上海原油期货的价格可以快速地出现上涨或下降趋势,从而满足市场供需要求,对价格形成支撑。不仅在对冲风险方面对市场参与者友好,而且在优化资源配置方面,上海原油期货市场为产业客户提供了新的资源配置渠道。市场参与者评价上海原油期货“上海价格不仅对参与交易的买方和卖方而言是合理的、有意义的,对生产商和终端消费者也是如此”。因此,针对于反映在上海原油期货中的原油商品属性,采用我国的原油生产量和原油进口量指标,作为原油期货的供给。
由于上海原油期货价格本质上是一个到岸价格,因此相对更能反映炼厂加工成本的变化。在运费市场大幅波动的情况下,代表装运港价格的境外原油价格变化一般不会反映这种差异,但是代表到货价格的上海原油期货价格的波动则涵盖了运费波动。这样相对之下,由于更能反映炼厂加工成本的变化,因此可以吸引更多的资源国、生产商、国际大石油公司、贸易商等以上海原油期货为基准进行报价。考虑到这个原因,原油期货的需求采用原油加工量和原油表观消费量指标。
4.1.2. 金融属性
原油期货以原油作为标的物进行交易,起着提供风险管理工具的作用。期货的标准化合约、保证金制度、结算制度,都揭示了期货与生俱来的金融属性。而金融属性大多跟宏观影响因素相关,比如汇率、政治、经济等。因此,在研究上海原油期货价格影响因素时,可以采用交易量和持仓量指标。
国际原油期货,比如布伦特原油期货、WTI原油期货和迪拜/阿曼原油期货,都是以美元进行计价结算。不过中国原油期货以人民币进行计价结算,因此一般情况下,中国货币政策和人民币币值的变化都会对中国原油期货的价格和操作产生影响。虽然目前人民币尚未实现国际化,跨境流动仍有许多限制。但是在研究上海原油期货的影响因素时,人民币汇率仍是不可或缺的。
根据上海国际能源交易中心相关公告,上海原油期货合约标的为中质含硫原油,可交割油种包括阿联酋迪拜原油、上扎库姆原油、阿曼原油、卡塔尔海洋油、也门马西拉原油、伊拉克巴士拉轻油,以及中国胜利原油。在国际原油期货中,迪拜原油和阿曼原油是含硫中质原油。布伦特原油可以作为西区的基准原油代表,而迪拜原油可以作为东区基准原油的代表。三大原油期货中,从距离上看,WTI和布伦特原油期货对应的实货资源运抵中国将比阿曼原油期货交割实物的距离远很多;从油种品质上看,WTI、布伦特原油和阿曼原油的品质差异也很大。因此,在跨区套利上,显然不必舍近求远,将上海原油期货价格与WTI、布伦特进行关联测算。同样在研究影响因素时,可以选用阿曼原油价格指标。
从宏观层面来说,中国经济数据的变化将会更加直观地体现在油价变化中,这种变化对上海原油期价的影响有目共睹。本文采用石油工业的生产者出厂价格指数和宏观经济景气指数来代表中国宏观层面对原油期货的影响。
4.1.3. 地缘政治因素
2014年,首次将地缘政治风险带入危机后经济分析的视野。在《世界经济展望》和《金融稳定报告》中,IMF都强调了地缘政治风险的威胁。
对于原油期货来说,地缘政治因素的影响尤其明显。虽然地缘政治风险很难量化,不像信用风险、债务风险、流动性风险和违约风险等,可以进行精准地度量。但是对于原油这种全球性战略物资而言,哪怕是区域性的地缘政治波动,特别是中东等产油国的政治动荡,对原油期货的冲击,乃至全球经济金融的冲击,都是不可忽视的。由于无法准确度量每次地缘政治动荡达到的影响程度,因此本文在地缘政治方面暂且不选取相应指标。
4.2. 影响因子指标构建
上海原油期货价格波动的影响因素,从商品属性与金融属性展开讨论,其指标的构建也从这两个方面入手。根据对影响因素的分析与选取,在考虑以供需为主的商品属性时,采用我国的原油生产量和原油进口量作为原油期货的供给。由于我国原油生产量很小,基本依靠进口,所以合并原油生产量和原油进口量两个指标为原油供给量。而原油期货的需求采用原油加工量和原油表观消费量指标。在考虑金融属性时,采用原油期货自身的交易量和持仓量指标,以及人民币汇率和阿曼原油价格。另外,石油工业的生产者出厂价格指数和宏观经济景气指数来代表中国宏观层面对原油期货的影响。上海原油期货价格变动影响因素见表1。

Table 1. Influencing factors of Shanghai crude oil futures price changes
表1. 上海原油期货价格变动影响因素表
4.3. 主成分分析法
上海原油期货的影响因素通过以上分析,选取九个指标,依托主成分模型,提取主成分。
由于上海原油期货上市于2018年3月26日,因此选取数据的时间段开始于2018年4月。因受限于某些宏观指标的统计延迟,数据截止至2019年12月。数据来源于中经数据库,国泰安数据库,RESSET数据库。
运用SPSS软件进行主成分分析,对原来的指标进行标准化,以消除变量在水平和量纲上的影响。然后进行KMO和Bartlett球形度检验,判断是否适合做主成分分析。

Table 2. KMO and Bartlett inspection
表2. KMO和巴特利特检验
一般情况下,KMO值大于0.5,基本适合主成分分析法。由表2可知,KMO值为0.733,大于0.5,说明指标数据符合做主成分分析的要求。Bartlett球形度检验近似卡方为182.010,显著性为0.000,小于0.05的显著性水平,可以拒绝Bartlett球形度检验的原假设。因此,通过KMO和Bartlett球形度检验,可以判断本文选取的上海原油期货影响因素指标组适合做主成分分析。

Table 3. Common factor variance table
表3. 公因子方差表
关于公因子方差表,即表3。展示了所有指标数据的共同方差。初始解下的变量共同度表明,对原有指标采用主成分分析法提取所有9个特征根,则原有的所有方差都可以被解释,因为变量的共同度均为1,也就是原有变量标准化后的方差为1。设定主成分分析法按照指定的提取条件提取特征根,即指定特征根大于1进行提取,给出提取特征根的共同度,可以看出所有变量都提取了70%及以上的信息,即所有变量的大部分信息都可以被主成分解释,变量信息丢失较少。因此本次主成分提取的总体效果理想。
表4给出的是各成分的方差贡献率和累计贡献率。提取主成分的方法有两种,一是根据大于1的特征值的个数确定主成分的个数;二是根据主成分的累计贡献率确定主成分的个数,使累计贡献率大于80%。在本文中,根据大于1的特征值的个数确定主成分的个数。由表可知,前2个特征根λ大于1,因此提取了前两个主成分。第一主成分的方差所占所有主成分方差的62.851%,超过一半,前两个主成分的方差贡献率达到76.165%,基本可以解释指标变量的大部分信息及涵盖上海原油期货价格波动的影响因素。

Table 5. Rotated component matrix
表5. 旋转后的成分矩阵
表5输出为旋转后的主成分矩阵,也就是载荷矩阵,表示主成份与标准化原始变量之间的相关系数矩阵,相关系数即各主成分在各变量上的载荷。旋转方法采用凯撒正态化最大方差法,旋转在3次迭代后已收敛。第一主成分包括原油供给量,原油表观消费量,阿曼原油价格,生产者出厂价格指数,宏观经济景气指数。第二主成分包括原油加工量,交易量,持仓量,人民币汇率。
每一个数代表的是线性相关系数,如0.881表示第1个主成分和原油供给量之间的线性相关系数。每一行代表的是主成分对于原始变量的贡献率,以第一行为例,表示所提取的主成分对于变量原油供给量的贡献率为:
,与公因子方差表比较可知,0.841就是原油供给量被提取的信息比例。每一列代表的是提取主成分的特征值。以第一列为例:
。

Table 6. Component score coefficient matrix
表6. 成分得分系数矩阵
表6给出的是标准化之后的主成分的得分系数矩阵,即特征向量。大部分学者认为,该表可以获得标准化主成份的计算公式,例如:标准化主成分F1 = 0.282 * 标准化原油供给量 + 0.270 * 标准化原油表观消费量 + … + (−139) * 标准化宏观经济景气指数。因此,可以得出标准化后的主成分公式:
通过主成分分析法,把九个指标,即原油供给量,原油表观消费量,原油加工量,交易量,持仓量,人民币汇率,阿曼原油价格,生产者出厂价格指数,宏观经济景气指数转化成两个主成分。从而使探究上海原油期货价格波动更简便。
5. 结语
本文通过讨论原油期货的商品属性和金融属性,剖析关于我国上海原油期货价格波动的影响因素。运用主成分分析法建立影响因子的指标体系,提取主成分进行研究分析,对全面认识和把握我国原油期货市场的发展现状及其内在特征有一定的帮助,有利于进一步发展和完善我国石油期货市场,进一步体现石油期货的价格引导作用,从而提高我国原油期货市场在国际市场上的话语权与影响力。
基金项目
教育部人文社科基金项目“中美经贸摩擦背景下临港经济风险预警与对冲策略研究:以山东半岛蓝色经济区为例”(19YJC790128)。