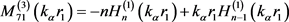半空间中具有非理想界面的圆柱形芯–壳结构对P波的多重衍射

doi:10.12677/IJM.2020.92006

期刊菜单

半空间中具有非理想界面的圆柱形芯–壳结构对P波的多重衍射
Multiple Diffraction of P Wave by Cylindrical Core-Shell Structure with Non-Ideal Interface in Half Space

DOI: 10.12677/IJM.2020.92006, PDF, HTML, XML, 下载: 482 浏览: 1,336 国家自然科学基金支持
作者: 郭静, 欧志英^*, 雷东侠：兰州理工大学，理学院，甘肃兰州
关键词: 弹簧模型；芯–壳结构；表面效应；动应力集中；Spring Model； Core-Shell Structure； Surface Effect； Dynamic Stress Concentration

摘要: 本文应用波函数展开法分析了半空间中具有非理想界面的圆柱形芯–壳结构对平面P波的多重衍射，得到了动应力集中因子的解析解。采用弹簧模型模拟非理想界面，通过改变材料参数，弹簧系数及入射角度，讨论在不同入射波频率下动应力集中因子的变化情况。结果表明：在纳米尺度下，表面参数对界面处的动应力集中程度有显著影响；增大弹簧的弹性系数时，界面处动应力集中因子与理想界面的动应力集中因子相接近；改变入射波的频率与角度，动应力集中因子也有明显不同。针对不同的实际问题使用不同的弹簧模型模拟不完美界面，可以使问题的研究结果更加精确。

Abstract: In this paper, the wave function expansion method is used to analyze the multiple diffraction of plane P wave by cylindrical core-shell structure with non-ideal interface in half space, and the an-alytical solution of dynamic stress concentration factor is obtained. A spring model is used to sim-ulate the non-ideal interface. By changing the material parameters, spring coefficient and incident angle, the variation of dynamic stress concentration factor at different incident wave frequencies is discussed. The results show that the surface parameters have a significant effect on the dynamic stress concentration at the interface at the nanometer scale. The dynamic stress concentration factor at the interface is close to that at the ideal interface by increasing the elastic coefficient of the spring. When the frequency and angle of incident wave are changed, the dynamic stress con-centration factor is obviously different. Using different spring models to simulate the imperfect interface for different practical problems can make the research results more accurate.

文章引用：郭静, 欧志英, 雷东侠. 半空间中具有非理想界面的圆柱形芯–壳结构对P波的多重衍射[J]. 力学研究, 2020, 9(2): 48-60. https://doi.org/10.12677/IJM.2020.92006

1. 研究背景

随着纳米技术的发展，纳米复合材料越来越受到工业和材料科学研究者的重视。并且纳米复合材料已被证明其具有优异的力学和物理性能 [1] [2]，这些性能可以使材料具有更多的功能。尽管到目前为止纳米复合材料已经取得了很多进步，但在材料的减振方面还需要更多的仔细研究。我们知道振动会引起弹性波在材料中传播 [3]，复合材料中通过夹杂物对波的散射，可以在很大程度上使波衰减。

因此，研究夹杂物对弹性波的散射问题非常重要的，这一课题的研究最早是由White等人 [4] 提出。Stamos等人 [5] 通过坐标变换法与积分变换法，有效地将三维空间中的动应力集中问题转化为二维问题，并用此方法研究了半空间中无限长隧道对地震波的动应力集中问题。Gubernatis等人 [6] 利用积分方程推导出各向同性弹性介质中单一均匀夹杂对平面波散射的波函数表达式。Liu等人 [7] [8] [9] 利用复变函数法求解了弹性波的散射问题，并对多个模型进行分析。Jain等人 [10] [11] 采用波函数展开法讨论了圆柱形夹杂和球体夹杂对弹性波的散射问题。Yi等人 [12] 采用波函数展开法，研究了入射波频率和入射波与隧道距离对隧道的影响，结果发现，低频入射波相比于高频入射波，具有更大的动应力强度因子。Wang等人 [13] 应用有限元的方法研究了圆形隧道受到地震波引起的应力增量。Wang等人 [14] 研究了弹性固体中两个纳米圆形孔对平面纵波的多重衍射，结果表明，当孔的半径减小到纳米尺度时，表面能对弹性波的衍射有显著影响。Ou等人 [15] 研究了两种具有界面效应的圆柱形纤维对平面纵波的散射，得到了不同入射频率下纤维与基体界面处的动应力集中系数。又在表面弹性理论的框架下，研究了嵌入弹性基体中的单纳米涂层光纤对平面纵波和横波的散射，并进行了数值计算 [16]。

以上研究内容都是在理想界面的情况下研究的，在实际问题中，非理想界面更为常见。张等人 [17] 采用傅里叶级数展开法，研究了凸起地形的混合边值问题。Valier-Brasier等人 [18] 利用弹簧模型对非理想固–固界面中界面波的尺度行为进行了讨论。Fang等人 [19] 结合波函数展开法和保角变换方法，研究了非圆隧道的应力集中情况，给出了非理想界面上的应力的分布情况，详细讨论了非理想界面与入射波长的相互作用，从而提出了提高隧道强度的有效方法。Yi等人 [20] 研究平面纵波作用下非完美界面圆衬砌隧道动力响应的理论方法，结果表明，界面刚度的变化对岩石和衬砌中动应力集中系数的分布有较大的影响。与低频入射波相比，高频入射波作用下，界面的不完美性对岩体及衬砌结构的动应力集中因子影响更为显著。Fang等人 [21] 对部分脱粘管道在P波和SV波作用下的动态裂纹张开位移进行了预测，并建立了相应的数学模型，通过满足考虑裂纹的边界条件来确定扩展系数。

从上述文献可以看出，虽然目前在夹杂物对弹性波散射问题的研究领域已取得了一些成果，但是对具有非理想界面的纳米芯–壳结构却没有研究。由于芯–壳结构是由两种及两种以上的材料组成，因此与单一纳米材料相比较，纳米芯–壳结构具有多种材料的优良性能与更加广泛的应用前景。在实际情况中，界面并不都是完美的、光滑的，总会以一定形式的缺陷存在着，因此，本文利用坐标变换法、波函数展开法以及三角函数的正交性研究了半空间中具有非理想界面的圆柱形芯–壳结构对平面P波的多重衍射，并分析了基体与涂层界面处的动应力集中因子。

2. 模型与公式

2.1. 模型建立

如图1所示，半空间内有一个具有非理想界面的纳米圆柱芯–壳结构，其外半径为a，内半径为b，与半平面距离为h，一束稳态入射平面P波以与y轴正方向夹角为 $θ_{α}$ 的方向入射，图中基体与芯–壳结构各层材料的弹性常数、剪切模量和质量体密度分别为 $λ^{(j)}$ ， $μ^{(j)}$ 和 $ρ^{(j)}$ $(j = 1, 2, 3)$ 。

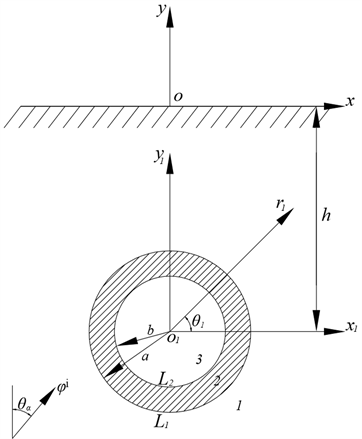
Figure 1. Multiple diffraction of P wave by cylindrical core-shell structure with non-ideal interface in half space

图1. 半空间中具有非理想界面的纳米芯–壳结构对入射P波的多重衍射

2.2. 波函数在不同坐标系下的基本方程

入射平面P波在坐标系 $(x, y)$ 下的波函数为：

$φ^{i} (x, y) = φ_{0} \exp [I k_{α 1} (x \sin θ_{α} + y \cos θ_{α}) - I ω t]$ (1)

其中 $φ_{0}$ 是入射P波的振幅，取 $φ_{0} = 1$ ，I是虚数单位， $k_{α 1} = ω / c_{p}^{(1)}$ 、 $c_{p}^{(1)} = \sqrt{(λ^{(1)} + 2 μ^{(1)}) / ρ^{(1)}}$ 分别是P波在基体中的波数和波速，t是时间因子。

当入射波与半空间的界面碰撞时，会有反射的有P波 $(φ)$ 和SV波 $(ψ)$ 形成，由半空间处应力自由可以得到相应的反射波函数在坐标系 $(x, y)$ 下可表示为：

$φ^{r} (x, y) = K_{1} \exp [I k_{α 1} (x \sin θ_{α} - y \cos θ_{α}) - I ω t]$ (2)

$ψ^{r} (x, y) = K_{1} \exp [I k_{β 1} (x \sin θ_{β} - y \cos θ_{β}) - I ω t]$ (3)

其中 $K_{1} = \frac{\sin 2 θ_{α} \sin 2 θ_{β} - κ^{2} \cos^{2} 2 θ_{β}}{\sin 2 θ_{α} \sin 2 θ_{β} + κ^{2} \cos^{2} 2 θ_{β}}$ ， $K_{2} = \frac{- 2 \sin 2 θ_{α} \cos 2 θ_{β}}{\sin 2 θ_{α} \sin 2 θ_{β} + κ^{2} \cos^{2} 2 θ_{β}}$ ， $K_{1}$ 、 $K_{2}$ 为反射波的系数， $κ = k_{β 1} / k_{α 1} = c_{α 1} / c_{β 1}$ ， $k_{β 1} = ω / c_{s}^{(1)}$ 、 $c_{s}^{(1)} = \sqrt{μ^{(1)} / ρ^{(1)}}$ 分别是SV波在基体中的波数和波速。

以下忽略时间因子，将式(1)~(3)利用波函数展开法在坐标系 $(r_{1}, θ_{1})$ 下表示为：

$φ^{i} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} J_{n} (k_{α 1} r_{1}) \exp (I n θ_{α} + I n θ_{1} - I k_{α 1} h \cos θ_{α})$ (4)

$φ^{r} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} {(- 1)}^{n} K_{1} J_{n} (k_{α 1} r_{1}) \exp (- I n θ_{α} + I n θ_{1} + I k_{α 1} h \cos θ_{α})$ (5)

$ψ^{r} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} {(- 1)}^{n} K_{2} J_{n} (k_{β 1} r_{1}) \exp (- I n θ_{β} + I n θ_{1} + I k_{β 1} h \cos θ_{β})$ (6)

其中 $J_{n} (\cdot)$ 是n阶第一类Bessel函数。

当入射波、反射波与芯–壳结构碰撞时，会产生散射波，相应的波函数为：

$φ^{s} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} A_{1 n} H_{n}^{(1)} (k_{α 1} r_{1}) \exp (I n θ_{1})$ (7)

$ψ^{s} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} B_{1 n} H_{n}^{(1)} (k_{β 1} r_{1}) \exp (I n θ_{1})$ (8)

其中 $A_{1 n}$ 和 $B_{1 n}$ 是基体中散射波的未知系数， $H_{n}^{(1)} (\cdot)$ 是n阶第一类Hankel函数。

由波的叠加原理可以得到基体中的总波场为：

$\begin{matrix} φ^{(1)} (r_{1}, θ_{1}) = φ^{i} (r_{1}, θ_{1}) + φ^{r} (r_{1}, θ_{1}) + φ^{s} (r_{1}, θ_{1}) \\ = \sum_{n = - \infty}^{+ \infty} [A_{0 n} J_{n} (k_{α 1} r_{1}) + A_{1 n} H_{n}^{(1)} (k_{α 1} r_{1})] \exp (I n θ_{1}) \end{matrix}$ (9)

$\begin{matrix} ψ^{(1)} (r_{1}, θ_{1}) = ψ^{r} (r_{1}, θ_{1}) + ψ^{s} (r_{1}, θ_{1}) \\ = \sum_{n = - \infty}^{+ \infty} [B_{0 n} J_{n} (k_{β 1} r_{1}) + B_{1 n} H_{n}^{(1)} (k_{β 1} r_{1})] \exp (I n θ_{1}) \end{matrix}$ (10)

其中 $A_{0 n} = \exp (I n θ_{α} - I k_{α 1} h \cos θ_{α}) + {(- 1)}^{n} K_{1} \exp (- I n θ_{α} + I k_{α 1} h \cos θ_{α})$ ， $B_{0 n} = {(- 1)}^{n} K_{2} \exp (- I n θ_{β} + I k_{β 1} h \cos θ_{β})$

涂层中的总波场为：

$φ^{(2)} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} [A_{2 n} J_{n} (k_{α 2} r_{1}) + C_{2 n} H_{n}^{(2)} (k_{α 2} r_{1})] \exp (I n θ_{1})$ (11)

$ψ^{(2)} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} [B_{2 n} J_{n} (k_{β 2} r_{1}) + D_{2 n} H_{n}^{(2)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (12)

其中 $A_{2 n}$ ， $B_{2 n}$ ， $C_{2 n}$ 和 $D_{2 n}$ 是涂层中的未知系数， $k_{α 2}$ 、 $k_{β 2}$ 、 $c_{p}^{(2)}$ 、 $c_{s}^{(2)}$ 分别是涂层中P波和SV波的波数和波速， $H_{n}^{(2)} (\cdot)$ 是n阶第二类Hankel函数。

芯体中的总波场为：

$φ^{(3)} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} A_{3 n} J_{n} (k_{α 3} r_{1}) \exp (I n θ_{1})$ (13)

$ψ^{(3)} (r_{1}, θ_{1}) = \sum_{n = - \infty}^{+ \infty} B_{3 n} J_{n} (k_{β 3} r_{1}) \exp (I n θ_{1})$ (14)

其中 $A_{3 n}$ 和 $B_{3 n}$ 是芯体中的未知系数， $k_{α 3}$ 、 $k_{β 3}$ 、 $c_{p}^{(3)}$ 、 $c_{s}^{(3)}$ 以及 $k_{β 3}$ 和 $c_{s}^{(3)}$ 分别是芯体中P波和SV波的波数和波速。

由圆柱坐标系中，位移与位移势的关系为：

$u_{r} = \frac{\partial φ}{\partial r} + \frac{1}{r} \frac{\partial ψ}{\partial θ}$ (15)

$u_{θ} = \frac{1}{r} \frac{\partial φ}{\partial θ} - \frac{\partial ψ}{\partial r}$ (16)

以及相应的应力与位移势的关系为：

$σ_{r r} = λ (\frac{\partial^{2} φ}{\partial r^{2}} + \frac{1}{r} \frac{\partial φ}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} φ}{\partial θ^{2}}) + 2 μ (\frac{\partial^{2} φ}{\partial r^{2}} - \frac{1}{r^{2}} \frac{\partial ψ}{\partial θ} + \frac{1}{r} \frac{\partial^{2} ψ}{\partial r \partial θ})$ (17)

$σ_{θ θ} = λ (\frac{\partial^{2} φ}{\partial r^{2}} + \frac{1}{r} \frac{\partial φ}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} φ}{\partial θ^{2}}) + 2 μ (\frac{1}{r^{2}} \frac{\partial^{2} φ}{\partial θ^{2}} + \frac{1}{r} \frac{\partial φ}{\partial r} - \frac{1}{r} \frac{\partial^{2} ψ}{\partial r \partial θ} + \frac{1}{r^{2}} \frac{\partial ψ}{\partial θ})$ (18)

$σ_{r θ} = \frac{μ}{r} (2 \frac{\partial^{2} φ}{\partial r \partial θ} - \frac{2}{r} \frac{\partial φ}{\partial θ} + \frac{1}{r} \frac{\partial^{2} ψ}{\partial θ^{2}} - r \frac{\partial^{2} ψ}{\partial r^{2}} + \frac{\partial ψ}{\partial r})$ (19)

将式(9)~(14)代入式(15)~(19)中，可以得到基体、涂层及芯体中的位移场与应力场分别为：

$u_{r_{1}}^{(1)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [A_{0 n} M_{71}^{(1)} (k_{α 1} r_{1}) + A_{1 n} M_{71}^{(3)} (k_{α 1} r_{1}) + I B_{0 n} M_{72}^{(1)} (k_{β 1} r_{1}) + I B_{1 n} M_{72}^{(3)} (k_{β 1} r_{1})] \exp (I n θ_{1})$ (20)

$u_{θ_{1}}^{(1)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [I A_{0 n} M_{81}^{(1)} (k_{α 1} r_{1}) + I A_{1 n} M_{81}^{(3)} (k_{α 1} r_{1}) + B_{0 n} M_{82}^{(1)} (k_{β 1} r_{1}) + B_{1 n} M_{82}^{(3)} (k_{β 1} r_{1})] \exp (I n θ_{1})$ (21)

$σ_{r_{1} r_{1}}^{(1)} = \frac{2 μ^{(1)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{0 n} E_{11}^{(1)} (k_{α 1} r_{1}) + A_{1 n} E_{11}^{(3)} (k_{α 1} r_{1}) + I B_{0 n} E_{12}^{(1)} (k_{β 1} r_{1}) + I B_{1 n} E_{12}^{(3)} (k_{β 1} r_{1})] \exp (I n θ_{1})$ (22)

$σ_{θ_{1} θ_{1}}^{(1)} = \frac{2 μ^{(1)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{0 n} E_{21}^{(1)} (k_{α 1} r_{1}) + A_{1 n} E_{21}^{(3)} (k_{α 1} r_{1}) + I B_{0 n} E_{22}^{(1)} (k_{β 1} r_{1}) + I B_{1 n} E_{22}^{(3)} (k_{β 1} r_{1})] \exp (I n θ_{1})$ (23)

$σ_{r_{1} θ_{1}}^{(1)} = \frac{2 μ^{(1)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [I A_{0 n} E_{41}^{(1)} (k_{α 1} r_{1}) + I A_{1 n} E_{41}^{(3)} (k_{α 1} r_{1}) + B_{0 n} E_{42}^{(1)} (k_{β 1} r_{1}) + B_{1 n} E_{42}^{(3)} (k_{β 1} r_{1})] \exp (I n θ_{1})$ (24)

$u_{r_{1}}^{(2)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [A_{2 n} M_{71}^{(1)} (k_{α 2} r_{1}) + C_{2 n} M_{71}^{(4)} (k_{α 2} r_{1}) + I B_{2 n} M_{72}^{(1)} (k_{β 2} r_{1}) + I D_{2 n} M_{72}^{(4)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (25)

$u_{θ_{1}}^{(2)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [I A_{2 n} M_{81}^{(1)} (k_{α 2} r_{1}) + I C_{2 n} M_{81}^{(4)} (k_{α 2} r_{1}) + B_{2 n} M_{82}^{(1)} (k_{β 2} r_{1}) + D_{2 n} M_{82}^{(4)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (26)

$σ_{r_{1} r_{1}}^{(2)} = \frac{2 μ^{(2)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{2 n} E_{11}^{(1)} (k_{α 2} r_{1}) + C_{2 n} E_{11}^{(4)} (k_{α 2} r_{1}) + I B_{2 n} E_{12}^{(1)} (k_{β 2} r_{1}) + I D_{2 n} E_{12}^{(4)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (27)

$σ_{θ_{1} θ_{1}}^{(2)} = \frac{2 μ^{(2)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{2 n} E_{21}^{(1)} (k_{α 2} r_{1}) + C_{2 n} E_{21}^{(4)} (k_{α 2} r_{1}) + I B_{2 n} E_{22}^{(1)} (k_{β 2} r_{1}) + I D_{2 n} E_{22}^{(4)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (28)

$σ_{r_{1} θ_{1}}^{(2)} = \frac{2 μ^{(2)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [I A_{2 n} E_{41}^{(1)} (k_{α 2} r_{1}) + I C_{2 n} E_{41}^{(4)} (k_{α 2} r_{1}) + B_{2 n} E_{42}^{(1)} (k_{β 2} r_{1}) + D_{2 n} E_{42}^{(4)} (k_{β 2} r_{1})] \exp (I n θ_{1})$ (29)

$u_{r_{1}}^{(3)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [A_{3 n} M_{71}^{(1)} (k_{α 3} r_{1}) + I B_{3 n} M_{72}^{(1)} (k_{β 3} r_{1})] \exp (I n θ_{1})$ (30)

$u_{θ_{1}}^{(3)} = \frac{1}{r_{1}} \sum_{n = - \infty}^{\infty} [I A_{3 n} M_{81}^{(1)} (k_{α 3} r_{1}) + B_{3 n} M_{82}^{(1)} (k_{β 3} r_{1})] \exp (I n θ_{1})$ (31)

$σ_{r_{1} r_{1}}^{(3)} = \frac{2 μ^{(3)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{3 n} E_{11}^{(1)} (k_{α 3} r_{1}) + I B_{3 n} E_{12}^{(1)} (k_{β 3} r_{1})] \exp (I n θ_{1})$ (32)

$σ_{θ_{1} θ_{1}}^{(3)} = \frac{2 μ^{(3)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [A_{3 n} E_{21}^{(1)} (k_{α 3} r_{1}) + I B_{3 n} E_{22}^{(1)} (k_{β 3} r_{1})] \exp (I n θ_{1})$ (33)

$σ_{r_{1} θ_{1}}^{(3)} = \frac{2 μ^{(3)}}{r_{1}^{2}} \sum_{n = - \infty}^{\infty} [I A_{3 n} E_{41}^{(1)} (k_{α 3} r_{1}) + B_{3 n} E_{42}^{(1)} (k_{β 3} r_{1})] \exp (I n θ_{1})$ (34)

其中 $M_{i j}^{(k)}, E_{i j}^{(k)}$ 是波的变化函数(见附录)。

2.3. 边界条件

2.3.1. 位移边界条件

在界面 $r_{1} = a$ 与 $r_{1} = b$ 处，对于位移边界条件，本研究采用的线性弹簧模型对不完美界面进行模拟。该模型假设牵引力是连续的，而界面上的位移可能是不连续的。更精确地说，界面的不连续点的位移分量与它们各自的界面牵引力分量成比例。利用上述概念，位移边界条件为

$u_{r_{1}}^{(1)} - u_{r_{1}}^{(2)} = \frac{σ_{r_{1} r_{1}}^{(1)}}{k_{r_{1}}^{(1)}}, u_{θ_{1}}^{(1)} - u_{θ_{1}}^{(2)} = \frac{σ_{r_{1} θ_{1}}^{(1)}}{k_{θ_{1}}^{(1)}}, r_{1} = a$ (35)

$u_{r_{1}}^{(3)} - u_{r_{1}}^{(2)} = \frac{σ_{r_{1} r_{1}}^{(3)}}{k_{r_{1}}^{(3)}}, u_{θ_{1}}^{(3)} - u_{θ_{1}}^{(2)} = \frac{σ_{r_{1} θ_{1}}^{(3)}}{k_{θ_{1}}^{(3)}}, r_{1} = b$ (36)

2.3.2. 应力边界条件

由广义Young-Laplace方程(推导过程参考文献 [16])可以得到应力边界条件为

${\begin{cases} σ_{r_{1} r_{1}}^{(1)} - σ_{r_{1} r_{1}}^{(2)} = s_{1} (1 - ν^{(1)}) σ_{θ_{1} θ_{1}}^{(1)} - s_{1} ν^{(1)} σ_{r_{1} r_{1}}^{(1)} \\ σ_{r_{1} θ_{1}}^{(1)} - σ_{r_{1} θ_{1}}^{(2)} = - s_{1} (1 - ν^{(1)}) \frac{\partial σ_{θ_{1} θ_{1}}^{(1)}}{\partial θ_{1}} + s_{1} ν^{(1)} \frac{\partial σ_{r_{1} r_{1}}^{(1)}}{\partial θ_{1}} \end{cases}, r_{1} = a$ (37)

${\begin{cases} σ_{r_{1} r_{1}}^{(3)} - σ_{r_{1} r_{1}}^{(2)} = s_{2} (1 - ν^{(3)}) σ_{θ_{1} θ_{1}}^{(3)} - s_{2} ν^{(3)} σ_{r_{1} r_{1}}^{(3)} \\ σ_{r_{1} θ_{1}}^{(3)} - σ_{r_{1} θ_{1}}^{(2)} = - s_{2} (1 - ν^{(3)}) \frac{\partial σ_{θ_{1} θ_{1}}^{(3)}}{\partial θ_{1}} + s_{2} ν^{(3)} \frac{\partial σ_{r_{1} r_{1}}^{(3)}}{\partial θ_{1}} \end{cases}, r_{1} = b$ (38)

$s_{1} = \frac{2 μ^{s} + λ^{s}}{2 μ^{(2)} a}, s_{2} = \frac{2 μ^{s} + λ^{s}}{2 μ^{(2)} b} = η s_{1}, η = \frac{a}{b}$ (39)

其中， $s_{1}$ ， $s_{2}$ 为纳米尺度下衡量表面效应的无量纲参数。

将式(20)~(34)代入边界条件(35)~(39)中，利用三角函数的正交性，在等式两端同乘 $\exp (I m θ_{1})$ 并在 $[- π, π]$ 上积分得到线性方程组

$\begin{array}{l} A_{0 n} M_{71}^{(1)} (k_{α 1} a) + A_{1 n} M_{71}^{(3)} (k_{α 1} a) + I B_{0 n} M_{72}^{(1)} (k_{β 1} a) + I B_{1 n} M_{72}^{(3)} (k_{β 1} a) \\ - (A_{2 n} M_{71}^{(1)} (k_{α 2} a) + C_{2 n} M_{71}^{(4)} (k_{α 2} a) + I B_{2 n} M_{72}^{(1)} (k_{β 2} a) + I D_{2 n} M_{72}^{(4)} (k_{β 2} a)) \\ = \frac{2 μ^{(1)}}{k_{r_{1}}^{(1)} a} (A_{0 n} E_{11}^{(1)} (k_{α 1} a) + A_{1 n} E_{11}^{(3)} (k_{α 1} a) + I B_{0 n} E_{12}^{(1)} (k_{β 1} a) + I B_{1 n} E_{12}^{(3)} (k_{β 1} a)) \end{array}$ (40)

$\begin{array}{l} I A_{0 n} M_{81}^{(1)} (k_{α 1} a) + I A_{1 n} M_{81}^{(3)} (k_{α 1} a) + B_{0 n} M_{82}^{(1)} (k_{β 1} a) + B_{1 n} M_{82}^{(3)} (k_{β 1} a) \\ - (I A_{2 n} M_{81}^{(1)} (k_{α 2} a) + I C_{2 n} M_{81}^{(4)} (k_{α 2} a) + B_{2 n} M_{82}^{(1)} (k_{β 2} a) + D_{2 n} M_{82}^{(4)} (k_{β 2} a)) \\ = \frac{2 μ^{(1)}}{k_{θ_{1}}^{(1)} a} (I A_{0 n} E_{41}^{(1)} (k_{α 1} a) + I A_{1 n} E_{41}^{(3)} (k_{α 1} a) + B_{0 n} E_{42}^{(1)} (k_{β 1} a) + B_{1 n} E_{42}^{(3)} (k_{β 1} a)) \end{array}$ (41)

$\begin{array}{l} I A_{3 n} M_{81}^{(1)} (k_{α 3} b) + B_{3 n} M_{82}^{(1)} (k_{β 3} b) \\ - (I A_{2 n} M_{81}^{(1)} (k_{α 2} b) + I C_{2 n} M_{81}^{(4)} (k_{α 2} b) + B_{2 n} M_{82}^{(1)} (k_{β 2} b) + D_{2 n} M_{82}^{(4)} (k_{β 2} b)) \\ = \frac{2 μ^{(3)}}{k_{θ_{1}}^{(3)} b} (I A_{3 n} E_{41}^{(1)} (k_{α 3} b) + B_{3 n} E_{42}^{(1)} (k_{β 3} b)) \end{array}$ (42)

$\begin{array}{l} (A_{0 n} E_{11}^{(1)} (k_{α 1} a) + A_{1 n} E_{11}^{(3)} (k_{α 1} a) + I B_{0 n} E_{12}^{(1)} (k_{β 1} a) + I B_{1 n} E_{12}^{(3)} (k_{β 1} a)) \\ - \frac{μ^{(2)}}{μ^{(1)}} (A_{2 n} E_{11}^{(1)} (k_{α 2} a) + C_{2 n} E_{11}^{(4)} (k_{α 2} a) + I B_{2 n} E_{12}^{(1)} (k_{β 2} a) + I D_{2 n} E_{12}^{(4)} (k_{β 2} a)) \\ = s_{1} (1 - ν^{(1)}) (A_{0 n} E_{21}^{(1)} (k_{α 1} a) + A_{1 n} E_{21}^{(3)} (k_{α 1} a) + I B_{0 n} E_{22}^{(1)} (k_{β 1} a) + I B_{1 n} E_{22}^{(3)} (k_{β 1} a)) \\ - s_{1} ν^{(1)} (A_{0 n} E_{11}^{(1)} (k_{α 1} a) + A_{1 n} E_{11}^{(3)} (k_{α 1} a) + I B_{0 n} E_{12}^{(1)} (k_{β 1} a) + I B_{1 n} E_{12}^{(3)} (k_{β 1} a)) \end{array}$ (44)

$\begin{array}{l} (I A_{0 n} E_{41}^{(1)} (k_{α 1} a) + I A_{1 n} E_{41}^{(3)} (k_{α 1} a) + B_{0 n} E_{42}^{(1)} (k_{β 1} a) + B_{1 n} E_{42}^{(3)} (k_{β 1} a)) \\ - \frac{μ^{(2)}}{μ^{(1)}} (I A_{2 n} E_{41}^{(1)} (k_{α 2} a) + I C_{2 n} E_{41}^{(4)} (k_{α 2} a) + B_{2 n} E_{42}^{(1)} (k_{β 2} a) + D_{2 n} E_{42}^{(4)} (k_{β 2} a)) \\ = - I n s_{1} (1 - ν^{(1)}) (I A_{0 n} E_{21}^{(1)} (k_{α 1} a) + I A_{1 n} E_{21}^{(3)} (k_{α 1} a) + B_{0 n} E_{22}^{(1)} (k_{β 1} a) + B_{1 n} E_{22}^{(3)} (k_{β 1} a)) \\ + I n s_{1} ν^{(1)} (I A_{0 n} E_{11}^{(1)} (k_{α 1} a) + I A_{1 n} E_{11}^{(3)} (k_{α 1} a) + B_{0 n} E_{12}^{(1)} (k_{β 1} a) + B_{1 n} E_{12}^{(3)} (k_{β 1} a)) \end{array}$ (45)

$\begin{array}{l} (A_{3 n} E_{11}^{(1)} (k_{α 3} b) + I B_{3 n} E_{12}^{(1)} (k_{β 3} b)) \\ - \frac{μ^{(2)}}{μ^{(3)}} (A_{2 n} E_{11}^{(1)} (k_{α 2} b) + C_{2 n} E_{11}^{(4)} (k_{α 2} b) + I B_{2 n} E_{12}^{(1)} (k_{β 2} b) + I D_{2 n} E_{12}^{(4)} (k_{β 2} b)) \\ = s_{2} (1 - ν^{(3)}) (A_{3 n} E_{21}^{(1)} (k_{α 3} b) + I B_{3 n} E_{22}^{(1)} (k_{β 3} b)) - s_{2} ν^{(3)} (A_{3 n} E_{11}^{(1)} (k_{α 3} b) + I B_{3 n} E_{12}^{(1)} (k_{β 3} b)) \end{array}$ (46)

$\begin{array}{l} (I A_{3 n} E_{41}^{(1)} (k_{α 3} b) + B_{3 n} E_{42}^{(1)} (k_{β 3} b)) \\ - \frac{μ^{(2)}}{μ^{(3)}} (I A_{2 n} E_{41}^{(1)} (k_{α 2} b) + I C_{2 n} E_{41}^{(4)} (k_{α 2} b) + B_{2 n} E_{42}^{(1)} (k_{β 2} b) + D_{2 n} E_{42}^{(4)} (k_{β 2} b)) \\ = - I n s_{2} (1 - ν^{(3)}) (I A_{3 n} E_{21}^{(1)} (k_{α 3} b) + B_{3 n} E_{22}^{(1)} (k_{β 3} b)) + I n s_{2} ν^{(3)} (I A_{3 n} E_{11}^{(1)} (k_{α 3} b) + B_{3 n} E_{12}^{(1)} (k_{β 3} b)) \end{array}$ (47)

2.4. 数值结果与分析

应力集中因子指的是在一个不连续区域里的最大应力与标准局部应力的比值，是一个局部区域中应力集中严重程度的度量标准。半空间中具有非理想界面的纳米圆柱芯–壳结构涂层界面处的动应力集中因子DSCF定义为：

$DSCF = | \frac{σ_{θ_{1} θ_{1}}^{(1)}}{σ_{0}} |$ (48)

其中 $σ_{0} = - μ^{(1)} k_{β 1}^{2}$ 表示入射波产生的最大静应力值。

以下通过取不同材料参数来研究入射波的入射角，入射波的频率，弹簧系数对动应力集中因子的影响。在考虑表面效应和弹簧模型之后，DSCF不仅与入射波波数有关，而且与表面参数和弹簧系数有关。

在图2中，取 $k = \infty$ ，此时不考虑界面的不完美性，由圣维南原理取 $h = 8$ ，结果Ou等人的结果一致，验证了本文结论的可行性。从而再考虑弹簧模型因素，取低频 $k_{α 1} a = 0.2$ 时，观察表面效应参数 $s_{1}$ 的变化对动应力集中因子的影响。随着 $s_{1}$ 的增大，最大DSCF也在增大。

在图3中，考虑以低频 $k_{α 1} a = 0.2$ ，入射角为 $θ_{α} = 1.5$ 时入射，弹簧系数k的变化对动应力集中因子的影响。从图中可以看到，随着k的增大，DSCF趋于稳定，说明界面与理想界面越接近。

在图4中，考虑以低频 $k_{α 1} a = 0.2$ ，入射角为 $θ_{α} = 0.1$ 时入射，弹簧系数k的变化对动应力集中因子的影响。从图中可以看到，随着k的增大，DSCF趋于稳定。与图3比较可得，当入射角的不同时，不仅同一位置的DSCF有明显变化，而且最大DSCF也明显增大。

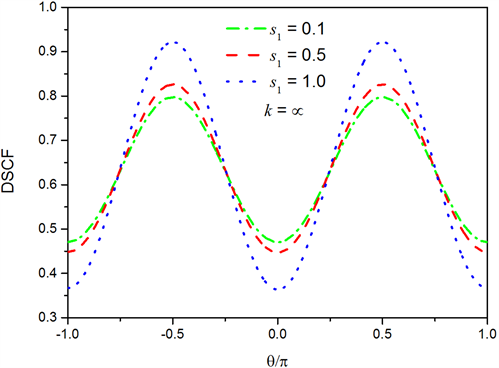
Figure 2. Influence of surface parameter $s_{1}$ on DSCF, when $k_{α 1} a = 0.2$ and $θ_{α} = 0.1$

图2. 波数 $k_{α 1} a = 0.2$ ， $θ_{α} = 0.1$ 时，表面参数 $s_{1}$ 对DSCF的影响

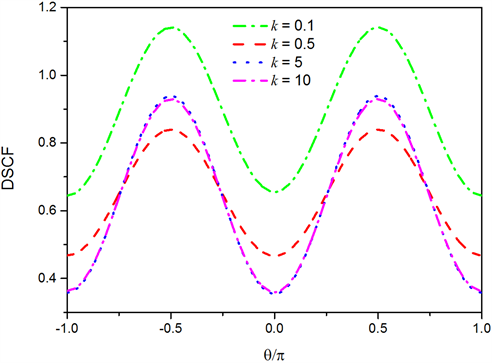
Figure 3. Influence of spring coefficient k on DSCF, when $k_{α 1} a = 0.2$ and $θ_{α} = 1.5$

图3. 波数 $k_{α 1} a = 0.2$ ， $θ_{α} = 1.5$ 时，弹簧系数k对DSCF的影响

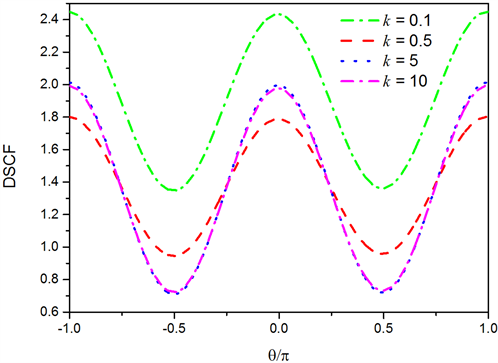
Figure 4. Influence of spring coefficient k on DSCF, when $k_{α 1} a = 0.2$ and $θ_{α} = 0.1$

图4. 波数 $k_{α 1} a = 0.2$ ， $θ_{α} = 0.1$ 时，弹簧系数k对DSCF的影响

在图5中，考虑高频 $k_{α 1} a = π$ 下，弹簧系数k的变化对动应力集中因子的影响。从图中可以看到，高频下由于波数增大，动应力集中因子相对低频比较敏感，所以DSCF会出现多个峰值，图像也更为复杂，而且高频下的动应力集中强度低于低频入射。

3. 结论

本文利用波函数展开法研究了半空间中具有非理想界面的纳米圆柱芯–壳结构对平面入射平面P波的多重衍射问题。通过对表面参数、入射波频率以及弹簧系数的不同取值，探讨了对应的动应力分布规律，

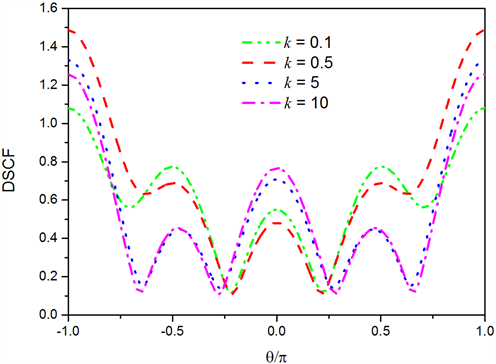
Figure 5. Influence of spring coefficient k on DSCF, when $k_{α 1} a = π$ and $θ_{α} = 1.5$

图5. 波数 $k_{α 1} a = π$ ， $θ_{α} = 1.5$ 时，弹簧系数k对DSCF的影响

分析了纳米尺度下表面效应和弹簧模型对环向应力的影响。结果表明：表面效应对动应力集中强度的影响显著；入射波的入射角度对动应力集中强度的影响显著；考虑表面效应之后，弹簧系数对动应力集中强度的影响也是不可忽略的。

基金项目

感谢国家自然科学基金和甘肃省自然科学基金(批准号：11362009，11862014)对本课题的支持

附录

$M_{71}^{(1)} (k_{α} r_{1}) = - n J_{n} (k_{α} r_{1}) + α r J_{n - 1} (k_{α} r_{1})$ $M_{72}^{(1)} (k_{β} r_{1}) = n J_{n} (k_{β} r_{1})$

$M_{81}^{(1)} (k_{α} r_{1}) = n J_{n} (k_{α} r_{1})$ $M_{82}^{(1)} (k_{β} r_{1}) = n J_{n} (k_{β} r_{1}) - k_{β} r_{1} J_{n - 1} (k_{β} r_{1})$

$M_{71}^{(4)} (k_{α} r_{1}) = - n H_{n}^{(2)} (k_{α} r_{1}) + k_{α} r_{1} H_{n - 1}^{(2)} (k_{α} r_{1})$ $M_{72}^{(4)} (k_{β} r_{1}) = n H_{n}^{(2)} (k_{β} r_{1})$

$M_{81}^{(4)} (k_{α} r_{1}) = n H_{n}^{(2)} (k_{α} r_{1})$ $M_{82}^{(4)} (k_{β} r_{1}) = n H_{n}^{(2)} (k_{β} r_{1}) - k_{β} r_{1} H_{n - 1}^{(2)} (k_{β} r_{1})$

$M_{72}^{(3)} (k_{β} r_{1}) = n H_{n}^{(1)} (k_{β} r_{1})$

$M_{81}^{(3)} (k_{α} r_{1}) = n H_{n}^{(1)} (k_{α} r_{1})$ $M_{82}^{(3)} (k_{β} r_{1}) = n H_{n}^{(1)} (k_{β} r_{1}) - k_{β} r_{1} H_{n - 1}^{(1)} (k_{β} r_{1})$

$E_{11}^{(1)} (k_{α} r_{1}) = (n^{2} + n - \frac{k_{β}^{2} r_{1}^{2}}{2}) J_{n} (k_{α} r_{1}) - k_{α} r_{1} J_{n - 1} (k_{α} r_{1})$

$E_{12}^{(1)} (k_{β} r_{1}) = - (n^{2} + n) J_{n} (k_{β} r_{1}) + n k_{β} r_{1} J_{n - 1} (k_{β} r_{1})$

$E_{11}^{(3)} (k_{α} r_{1}) = (n^{2} + n - \frac{k_{β}^{2} r_{1}^{2}}{2}) H_{n}^{(1)} (k_{α} r_{1}) - k_{α} r_{1} H_{n - 1}^{(1)} (k_{α} r_{1})$

$E_{12}^{(3)} (k_{β} r_{1}) = - (n^{2} + n) H_{n}^{(1)} (k_{β} r_{1}) + n k_{β} r_{1} H_{n - 1}^{(1)} (k_{β} r_{1})$

$E_{11}^{(4)} (k_{α} r_{1}) = (n^{2} + n - \frac{k_{β}^{2} r_{1}^{2}}{2}) H_{n}^{(2)} (k_{α} r_{1}) - k_{α} r_{1} H_{n - 1}^{(2)} (k_{α} r_{1})$

$E_{12}^{(4)} (k_{β} r_{1}) = - (n^{2} + n) H_{n}^{(2)} (k_{β} r_{1}) + n k_{β} r_{1} H_{n - 1}^{(2)} (k_{β} r_{1})$

$E_{41}^{(1)} (k_{α} r_{1}) = - (n^{2} + n) J_{n} (k_{α} r_{1}) + n k_{α} r_{1} J_{n - 1} (k_{α} r_{1})$

$E_{42}^{(1)} (k_{β} r_{1}) = (- n^{2} - n + \frac{k_{β}^{2} r_{1}^{2}}{2}) J_{n} (k_{β} r_{1}) + k_{β} r_{1} J_{n - 1} (k_{β} r_{1})$

$E_{42}^{(3)} (k_{β} r_{1}) = (- n^{2} - n + \frac{k_{β}^{2} r_{1}^{2}}{2}) H_{n}^{(1)} (k_{β} r_{1}) + k_{β} r_{1} H_{n - 1}^{(1)} (k_{β} r_{1})$

$E_{41}^{(4)} (k_{α} r_{1}) = - (n^{2} + n) H_{n}^{(2)} (k_{α} r_{1}) + n k_{α} r_{1} H_{n - 1}^{(2)} (k_{α} r_{1})$

$E_{42}^{(4)} (k_{β} r_{1}) = (- n^{2} - n + \frac{k_{β}^{2} r_{1}^{2}}{2}) H_{n}^{(2)} (k_{β} r_{1}) + k_{β} r_{1} H_{n - 1}^{(2)} (k_{β} r_{1})$

$E_{21}^{(1)} (k_{α} r_{1}) = (- n^{2} - n - \frac{k_{β}^{2} r_{1}^{2}}{2} + k_{α}^{2} r_{1}^{2}) J_{n} (k_{α} r_{1}) + k_{α} r_{1} J_{n - 1} (k_{α} r_{1})$

$E_{22}^{(1)} (k_{β} r_{1}) = (n^{2} + n) J_{n} (k_{β} r_{1}) - n k_{β} r_{1} J_{n - 1} (k_{β} r_{1})$

$E_{21}^{(3)} (k_{α} r_{1}) = (- n^{2} - n - \frac{k_{β}^{2} r_{1}^{2}}{2} + k_{α}^{2} r_{1}^{2}) H_{n}^{(1)} (k_{α} r_{1}) + k_{α} r_{1} H_{n - 1}^{(1)} (k_{α} r_{1})$

$E_{22}^{(3)} (k_{β} r_{1}) = (n^{2} + n) H_{n}^{(1)} (k_{β} r_{1}) - n k_{β} r_{1} H_{n - 1}^{(1)} (k_{β} r_{1})$

$E_{21}^{(4)} (k_{α} r_{1}) = (- n^{2} - n - \frac{k_{β}^{2} r_{1}^{2}}{2} + k_{α}^{2} r_{1}^{2}) H_{n}^{(2)} (k_{α} r_{1}) + k_{α} r_{1} H_{n - 1}^{(2)} (k_{α} r_{1})$

$E_{22}^{(4)} (k_{β} r_{1}) = (n^{2} + n) H_{n}^{(2)} (k_{β} r_{1}) - n k_{β} r_{1} H_{n - 1}^{(2)} (k_{β} r_{1})$

参考文献

[1]	Ramanathan, T., Liu H. and Brinson, L.C. (2005) Functionalized SWNT Polymer Nanocomposites for Dramatic Property Improvement. Journal of Polymer Science Part B, 43, 2269-2279. https://doi.org/10.1002/polb.20510
[2]	Ramanathan, T., Stankovich, S., Dikin, D.A., Liu, H., Shen, H., Nguyen, S.T. and Brinson, L.C. (2007) Graphitic Nanofillers in PMMA Nanocomposites: An In-vestigation of Particle Size and Dispersion and Their Influence on Nanocomposite Properties. Journal of Polymer Science Part B, 45, 2097-2112. https://doi.org/10.1002/polb.21187
[3]	Guz, I.A. and Rushchitsky, J.J. (2007) Computational Simulation of Har-monic Wave Propagation in Fibrous Micro- and Nanocomposites. Composites Science and Technology, 67, 861-866. https://doi.org/10.1016/j.compscitech.2006.01.032
[4]	White, R.M. (1958) Elastic Wave Scattering at a Cylindrical Discontinuity in a Solid. The Journal of the Acoustical Society of America, 30, 771-785. https://doi.org/10.1121/1.1909759
[5]	Stamos, A.A. and Beskos, D.E. (1996) 3-D Seismic Response Analysis of Long Lined Tunnels in Half-Space. Soil Dynamics and Earthquake Engineering, 15, 111-118. https://doi.org/10.1016/0267-7261(95)00025-9
[6]	Gubernatis, J.E., Domany, E. and Krumharlsl, J.A. (1977) Formal Aspects of the Theory of the Scattering of Ultrasound by Flaws in Elastic Materials. Journal of Applied Physics, 48, 2804-2811. https://doi.org/10.1063/1.324141
[7]	刘殿魁, 盖秉政, 陶贵源. 论孔附近的动应力集中[J]. 地震工程与工程振动, 1980(1): 99-112.
[8]	Liu, D.K., Gai, B.Z. and Tao, G.Y. (1982) Applications of the Method of Complex Functions to Dynamic Stress Concentrations. Wave Motion, 4, 293-304. https://doi.org/10.1016/0165-2125(82)90025-7
[9]	刘殿魁, 林宏伟. SH波散射与界面圆孔附近的动应力集中[J]. 力学学报, 1998, 30(5): 597-604.
[10]	Jain, D.L. and Kanwal, R.P. (1979) Scattering of Elastic Waves by Circular Cylindrical Flaws and Inclusions. Journal of Applied Physics, 50, 4067-4108. https://doi.org/10.1063/1.326489
[11]	Jain, D.L. and Kanwal, R.P. (1980) Scattering of Elastic Waves by Elastic Sphere. In-ternational Journal of Engineering Science, 18, 829-839. https://doi.org/10.1016/0020-7225(80)90029-4
[12]	Yi, C.P., Zhang, P., Johansson, D. and Nyberg, U. (2014) Dynamic Response of a Circular Lined Tunnel with an Imperfect Interface Subjected to Cylindrical P-Waves. Computers and Geotechnics, 55, 165-171. https://doi.org/10.1016/j.compgeo.2013.08.009
[13]	Wang, T.T., Hu, J.T., Chen, C.H. and Huang, T.H. (2014) Response of a Tunnel in Double Layer Rocks Subjected to Harmonic P- and S-Waves. International Journal of Rock Mechanics and Mining Sciences, 70, 435-443. https://doi.org/10.1016/j.ijrmms.2014.06.002
[14]	Wang, G.F. (2009) Multiple Diffraction of Plane Compressional Waves by Two Circular Cylindrical Holes with Surface Effects. Journal of Applied Physics, 105, 1-6. https://doi.org/10.1063/1.3054517
[15]	Ou, Z.Y. and Lee, D.W. (2012) Effects of Interface Energy on Multiple Scattering of Plane Compressional Waves by Two Cylindrical Fibers. International Journal of Applied Mechanics, 4, 1-19. https://doi.org/10.1142/S1758825112500408
[16]	Ou, Z.Y. and Lee, D.W. (2012) Effects of Interface Energy on Scattering of Plane Elastic Wave by a Nano-Sized Coated Fiber. Journal of Sound and Vibration, 331, 5623-5643. https://doi.org/10.1016/j.jsv.2012.07.023
[17]	张彦帅. 半圆弧凸起地形对平面P波的散射解析解[D]: [硕士学位论文]. 天津: 天津大学, 2004.
[18]	Valier-Brasier, T., Dehoux, T. and Bertrand, A. (2012) Scaled Behavior of Interface Waves at an Imperfect Solid-Solid Interface. Journal of Applied Physics, 112, 1-12. https://doi.org/10.1063/1.4733949
[19]	Fang, X.Q., Jin, H.X., Liu, J.X. and Huang, M.J. (2016) Imperfect Bonding Effect on Dynamic Response of a Non-Circular Lined Tunnel Subjected to Shear Waves. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 56, 226-231. https://doi.org/10.1016/j.tust.2016.03.008
[20]	Yi, C.P., Lu, W.B., Zhang, P., Johansson, D. and Nyberg, U. (2016) Effect of Imperfect Interface on the Dynamic Response of a Circular Lined Tunnel Impacted by Plane P-Waves. Tunneling and Underground Space Technology, 51, 68-74. https://doi.org/10.1016/j.tust.2015.10.011
[21]	Fang, X.Q., Huang, H.C. and Liu, J.X. (2016) Predicting the Crack Opening Displacements of a Partially Debonded Pipeline in Rock Mass under P Waves. Engineering Materials and Structures, 39, 886-895. https://doi.org/10.1111/ffe.12407

为你推荐

友情链接