1. 引言
不可积相位因子是解释A-B效应的关键,也是量子力学几何相位问题的关键。1986年殿村(A. Tonomura)的实验漂亮地证实了不可及相位因子的物理实在性 [1]。但是,有一些物理学家仍然质疑殿村实验和不可积相位因子的物理实在性,其中以主张磁矢量势为纯数学场的观点为主 [2]。
本文从量子力学中最基本的Schrödinger方程出发,简洁地导出A-B效应中的不可积相位因子。从理论分析上可以看到,被一些研究者忽略的一项 [2] 正是产生A-B效应的关键。从该理论出发也可以清晰地看出,A-B效应的本质原因正是微观客体的波粒二象性。
2. 不可积相因子的导出
在磁场中运动的电子的Hamilton量可以写成 [3]:
(1)
如果将磁场源放入无限长的超导筒中,将对磁场中运动电子和磁源系统本身动产生影响,因此Hamilton量中还应加入所有与之相关的势能项
,其中包括了超导电子间通过交换虚声子而产生的有效吸引势。因此,可以将磁场中运动电子和磁场源系统的Hamilton量分别写为 [2]:
(2)
(3)
其中
,
,其中
为别为不存在电子的时候磁场源的磁矢势和磁感应强度,
分别为磁场源系统中的电流分布和由此产生的无限长超导筒表面的屏蔽电流所产生的矢量势之和。
这样一来,整个体系的Hamilton量就可以写成:
(4)
将(2)、(3)两式带入(4)式之中并考虑
,
,可以得到:
整理之后可以得到:

这个Hamilton量满足Schrödinger方程,将其带入电子的Schrödinger方程之中并且考虑超导体的Meissner效应后可以将电子的Schrödinger方程等效为 [2]:
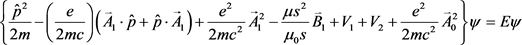 (6)
(6)
将(6)式与无磁场源时电子满足的Schrödinger方程
 (7)
(7)
相比较可以发现,在存在磁场的时候即使用超导筒将磁场源的作用屏蔽,依然会出现一项
。明显的这一项中
可以通过适当取势能零点而化简为零,所以这一项的全部物理意义应该在
之上。
再来从量子力学的最基本方程Schrödinger方程的角度来考虑。由于Schrödinger方程可以表示为:
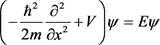
如果可以将波函数
通过某种变换,使得
在Schrödinger方程中不明显出现并且不改变波函数
的物理实际意义我们就可以得到与(7)式形式相同的方程,这样就可以更加明显地看到
的物理意义。
为了达到上述目的,将波函数写为:
(由于电子路径的任意性,积分变量设为
)。明显的,此时可以将(6)式写为:
(8)
可见(8)式与(7)式形式完全一样,而且
与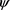 只差一个相位,二者在物理实际上等效。
只差一个相位,二者在物理实际上等效。
这样一来就从Schrödinger方程之中自然导出了A-B效应中的不可积相位 [4]
。
3. 理论分析
由于Schrödinger方程在量子力学中的基本地位,可以认为不可积相位因子形成的根源正是来自微观客体的波粒二象性。且由于电磁现象由不可积相位因子完全决定 [4],故A-B效应的原因正是不可积相因子及其中的磁矢势,这是由微观客体的波粒二象性决定的。这样一来也就不难从根源上理解不可积相位因子在物理学中占有重要地位的事实 [5] [6] [7]。
4. 结论
综上,从量子力学的基础方程Schrödinger方程出发,简洁地得出了A-B效应关键的不可积相位因子,说明了量子力学的波粒二象性正是产生A-B效应的本质原因,对一些报道中关于磁矢势的疑问做了初步的回答。进一步可以尝试从Dirac方程出发,通过类似的方法讨论不可积相位因子。由于不可积相位因子的概念贯穿于量子场论、规范场论以及高能物理、凝聚态物理的诸多相关理论之中,本文的结果对在科学研究中把握量子力学的基本特征也有一定的益处。