1. 引言
分布式网络是将网络资源分配给不同地区的节点处理,通过感知周围信息、计算处理信息等方式实现邻居节点的通信和信息传输。分布式网络中的某一个节点是一个硬件设备,例如传感器、计算机、机器人,甚至可以是一个线程或进程。分布式网络在处理进程任务时,通过调配网络中节点资源,分配给不同的节点处理不同计算、通信任务,这就可以实现将网络任务分解后,每个节点处理单一的分解小任务,提高处理速度 [1] [2]。虽然单台计算机的处理能力、存储能力等都在逐步提升,但仍然无法独立地处理复杂的任务,这就需要通过将多个计算设备、传感器等进行连接,构建分布式网络,满足日益增长的复杂问题处理需求,由此分布式网络计算也受到了越来越多的关注 [3]。
由于投影操作的存在,当本地的约束集合比较复杂时,甚至是本地约束由多个简单约束(如半平面或者球形约束)的交集组成时,分布式投影梯度法每一步中的投影操作计算代价会增大,对此学者提出了基于惩罚的方法,即每个节点的约束集均由惩罚函数与目标函数叠加合成,这将有约束的问题转化为无约束的问题,可以使用无约束的算法有效地求解,而不需要再进行投影操作。而这样做的缺点在于,这样的转化并不等效,二者最优值之间的间距由惩罚系数决定。此外考虑每个节点的本地约束集为多个简单约束交集的情况,采用了随机优化的方法,在每一步迭代中,每一个节点在本地的约束集中随机挑选一个简单约束进行投影,这有效减少了投影操作的计算代价,然而却会引起剧烈的震荡和缓慢的收敛速度。
由此提出了原对偶分离投影算法,每个节点只需要处理本地约束,这样有效地减少了计算代价。算法可以是确定性的,即本地约束被并行地处理,也可以是随机性的,即本地约束被随机采样进行处理。通过原对偶域以及分离投影的操作,算法都可以快速准确地收敛。
2. 问题提出
网络中假设包含了n个节点,用无向图
来表示。无中心分布式的有约束一直优化问题可以构建分布式网络来协同各个节点来解决,具体图下:
是节点i本地的约束集合,
是节点i本地的目标函数,
标石所有节点共有的优化变量,假设
可微且为凸函数,其由
个简单约束
交集构成。简单约束包括
范数球约束,以及半空间约束等等,他在求解投影是较为简单的,但多个简单约束的几何投影计算过程确实比较困难。由于网络全局协调是非中心节点来完成调度的,因此所有的全局问题都不会集中在中心节点上。任意的节点受限于内存、计算能力、隐私保护等,也不会获取得到整体问题的约束以及求解目标,由此本文设计的分布式算法主要通过找出复杂约束来求解得到最优解
。
3. 原有的分布式算法
分布式算法的求解研究主要源自集中式算法,通过拓展集中式算法来获取得到更好的分布式计算效率。无中心分布式一致优化问题大部分都是以无约束为基础,即表示每个节点的初始化节点为空,在当前的计算求解方式中可以划分为如下:
1) 原方法。大部分都是直接拓展原有的集中式处理方法,在迭代过程中会消耗更少的计算代价,但计算的收敛速度较低,求解计算得到的值精确度值普遍偏低。例如(次)梯度下降法 [4]、加速(次)梯度下降法 [5]、二阶方法 [6] 与对偶平均法 [7] [8]。
2) 原对偶方法。有研究学者在应用交替方向乘子法来构架分布式网络,它能够在理论上提供基础,实践后可知能够获取得到更好的收敛速度和精度,但迭代过程中每次都需要分析优化子问题,因此计算代价非常高。因此有学者为了解决上述计算代价高的问题,提出了近似方法,例二阶近似的ADMM精确一阶算法(EXTRA),这些算法具备非常好的收敛性,计算代价也相对较低。
约束的分布式优化问题中,分布式网络中任意的节点都会包含内在的约束集,因此求解方式也会存在以下方式:
1) 原方法。它是通过无约束算法上添加投影操作,也被称之为分布式投影(次)梯度法。即在每次迭代上都使应用任意的节点来实现本地目标的优化操作,并进一步的降低本地的(次)梯度,接下来则将计算得到估计值交换给邻据,融合两者之间的信息,最后将融合获取的结果都投影给本地约束集,并基于此来证明是否本地一致性,或者在本地约束不同来全连通图,由此来计算得到最优解集。
2) 原对偶方法。通过将原对偶方法拓展到有约束问题上。任意的节点会将所有的原变量估计值投影到相对应的约束集中,且保持对偶变馈一致。此外原对偶方法通过在投影在对偶域中给,但这些对偶并非是线性和非线性的约束,不是一致性得。因此可以在当前对偶变投影中计算得到最优解集,尤其是当前一些节点包含了本地约束后,也可以完成投影原域。
4. 原域的分布式随机投影法
本文应用梯度投影法分布式方法,提出了随机优化的策略。即在为
节点i在第i次迭代时的估计,在第k次迭代时,每个节点将自身的估计发送给自己的邻居,当节点i接收到自己的邻居
发送的
时,节点i进行如下两步操作:
步骤1:对接收到的邻居的估计进行信息融合:
(1)
其中
是网络对应的对称双随机矩阵W的i行j列的元素。
步骤2:融合本地目标的优化操作和邻据值,将融合获取的结果都投影给本地约束集,并基于此来证明是否本地一致性:
(2)
其中
代表在第k次迭代时的步长选择,而
是节点i的初始估计值,可以随机产生。
在式(1)中,
是节点i对于其本地估计值与其接受到的邻居估计值的加权平均,具体来说,
是节点i从其邻居
接收到的估计值
的权重,而所有权重之和为1,即
,对于并非节点i的邻居所有节点,
,我们设置
,使得节点
之间不能完成通信。在式(2)中,
首先着本地目标函数的梯度方向进行梯度下降,在此之后,节点i本应该进行
到其本地约束集
中的投影,然而,对于复杂的
投影的操作往往是难以计算的,为了减少计算代价,这里采取了随机的策略,即每次只在本地约束集中随机选取一个约束
进行投影,即
是从
中随机选取的。由于
,可能存在
其只是一个通过随机方法得到的近似值。
5. 数值实验
通过设计一个带多约束的分布式二次规划问题,然后随机生成不同连通度的网络来对比分析本文提出的原对偶算法性能。
1) 实验设置
考虑网络由
个节点,
条边组成,其中
代表网络的连通度。将分别在稀疏
和稠密
的网络(图1)中运行的算法。考虑一个带多约束的二次规划问题,优化变量
的维度
,每一个节点i都有各自的本地的二次的目标函数
其中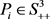 与
服从独立同分布的标准高斯分布。每一个节点i都包含
个本地约束,分别为
,
,
,其中
,
,
。它们分别代表
,
,与
范数球约束,以及多个半空间构成的多面体约束。
,
与
的值要保证问题的可行集不为空集。
与
服从独立同分布的标准高斯分布。每一个节点i都包含
个本地约束,分别为
,
,
,其中
,
,
。它们分别代表
,
,与
范数球约束,以及多个半空间构成的多面体约束。
,
与
的值要保证问题的可行集不为空集。
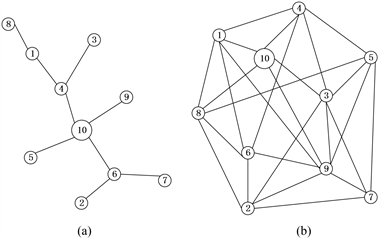
Figure 1. Network topologies with different connectivity degrees
. (a) Sparse network topology
; (b) Dense network topology
图1. 不同连通度
的网络拓扑。(a) 稀疏网络拓扑
;(b) 稠密网络拓扑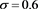
将比较以下四种算法的性能,即两种原域上的分布式随机投影法,以及提出的两种原对偶的分布式分离投影算法:
Constant RPJ:常数步长的随机投影算法,其中步长
取为常数。
Diminishing RPJ:递减步长的随机投影算法,步长
为递减的。
Deterministic PDSP:确定性原对偶分离投影算法。
Stochastic PDSP:随机性原对偶分离投影算法。
算法的性能将由最终距离最优解的相对误差来评估,第k次迭代后的误差被定义为
四种算法的性能比较结果显示在图2中。在稀疏网络中,Deterministci PDSP的参数为
;Stochastic PDSP的参数为
;Constant RPJ步长为0.02,Diminishing RPJ的步长为
,在稠密网络中的参数与稀疏网络中的参数几乎一致,除了Stochastic PDSP的
。

Figure 2. Performance comparison of the four algorithms. (a) Performance comparison of four algorithms in a dense network; (b) Performance comparison of four algorithms in sparse network
图2. 四种算法的性能比较。(a) 稠密网络中四种算法的性能比较;(b) 稀疏网络中四种算法的性能比较
从图2中可以观察到,两种原域的算法收敛速度较慢,精度较差,而提出两种原对偶算法性能在收敛速度和精度上的效果都更佳。比较两种原对偶分离算法,在稀疏网络中,确定性算法可以在700步迭代之内带到10−5的精度,而随机性算法需要4000步,可见确定性算法相比于随机性算法需要的迭代次数更少。而由于确定性算法需要在每一步迭代中处理所有的6个本地约束,而随机性算法只需要处理1个,因而随机性算法关于投影的计算代价是小于确定性算法的。同时观察到,相比于稀疏网络,确定性算法在稠密网络中得到了很好的加速,能够在300步迭代后达到10−5的精度,这是因为稠密网络中信息融合的速度更快。然而随机性算法在稀疏和稠密网络中的性能相差不大,认为这是每个节点在处理本地约束的随机性造成的。
6. 总结
在数据环境下,需要对海量数据进行分析处理,加快数据处理效率。分布式网络在处理进程任务时,通过调配网络中节点资源,分配给不同的节点处理不同计算、通信任务。无中心分布式一致优化问题大部分都是以无约束为基础,即表示每个节点的初始化节点为空。应用梯度投影法分布式方法,并提出了随机优化的策略。融合本地目标的优化操作,将融合获取的结果都投影给本地约束集,实验结果表明稠密网络中信息融合的速度更快。对于无中心分布式网络中的一致优化问题,我们在收敛性分析上只证明了确定性分离投影算法的收敛性,随机性的算法虽然在实验中显示了良好的效果,仍然需要理论上的保证。