应用子图划分策略的不确定图极大团枚举算法

An Enumeration Algorithm of the Maximal Cluster from the Uncertain Graph Using Subgraph Partition Strategy

摘要: 为了更加高效地枚举出不确定图极大团，通过对现有确定图和不确定图极大团枚举算法进行研究，结合在相同图结构下确定图极大团与不确定图极大团之间的关系，提出了一种基于相同图结构确定图极大团子图划分的高效不确定图极大团枚举算法D-MULE-D。通过在不同的真实数据集上进行实验测试，对比D-MULE-D算法和MULE算法的运行时间，验证D-MULE-D算法的可行性和高效性。

Abstract: In order to more efficiently enumerate maximal clique from the uncertain graph, by studying the existing algorithms of the maximal clique enumeration from the deterministic and uncertain graph, and according to the relationship of the maximal clique from the deterministic graph and the α-maximal clique from the uncertain graph under the same graph structure, an efficient enumeration algorithm of the α-maximal clique from the uncertain graph based on the subgraph partition of the maximal clique from the deterministic graph with the same graph structure, called D-MULE-D, is proposed in this paper. Experimental tests were carried out on different real data sets to verify the feasibility and efficiency of the D-MULE-D algorithm, by comparing the running time of the D-MULE-D algorithm with the MULE algorithm.

1. 引言

经过长年的研究发现，极大团枚举是一个NP-难问题，但通过广泛的实验验证，现有的确定图极大团枚举算法都能得到最终的极大团。然而在互联网技术的不断发展下，由于数据来源的异构性和数据描述手段的局限性，造成了图数据的不确定性，确定图的极大团枚举算法已不能满足实际生活中所获取的图数据的需求，因此不确定图极大团枚举算法已成为人们日益关注的焦点。在无线传感器网络中，由于通信信号干扰，导致通信链路的不确定性，图数据中边的连通性存在一定概率，因此无线传感器网络数据就可以模拟为不确定图；再如在蛋白质分子交互网络中，由于高通量生物实验的限制，蛋白质分子间是否存在相互作用具有不确定性，通过概率来量化这种交互关系的可能性，同样可以模拟出蛋白质分子交互的不确定图等等。在现实生活中，很多领域都对不确定图极大团枚举算法有着广泛的应用，如通信网络、生物网络、社交网络及web分析等。

近年来，随着大数据和互联网技术的快速发展，越来越多的科研人员致力于不确定图数据挖掘技术的研究，其中，不确定图极大团枚举算法的研究更是受到大家的普遍关注与重视。目前，不确定图极大团枚举算法主要有以下几类：1) 基于DFS的极大团枚举算法 [1]，此类算法是枚举极大团的基本方法，通过深度优先遍历所有顶点得到极大团，并应用回溯法过滤伪极大团，时间复杂度为O (n²·2ⁿ)；2) 基于简并顺序的极大团枚举算法 [2] [3] [4] [5]，此类算法是通过贪心思想遍历图中所有顶点后得到不确定图的简并顺序，根据此顺序来处理图中顶点得到极大团，时间复杂度为O (n²·2ⁿ)；3) 基于顶点编号升序的极大团枚举算法 [6] [7] [8]，此类算法是通过对不确定图中的顶点编号进行升序处理，通过增量计算维持两个顶点权值集合来枚举所有极大团，时间复杂度为O (n·2ⁿ)。通过比较三类极大团枚举算法，可以发现前两类算法已不适用于现实世界中超大规模的数据量，因此本文通过选择基于顶点编号升序的极大团枚举算法，并对此类算法中最典型的MULE算法 [9] 进行研究，提出了一种基于相同结构确定图极大团子图划分的高效不确定图极大团枚举算法——D-MULE-D，对于大规模数据的不确定图，应用MULE算法的时间复杂度是O (n·2ⁿ)，而应用D-MULE-D算法的时间复杂度是O (n·3^n/3)，该算法能够高效地得出最终的不确定图极大团。

本文下面的论述内容结构如下：首先通过问题定义，给出确定图极大团和不确定图极大团的定义，并根据定义，推导出在相同的结构下，确定图极大团与不确定图极大团的关系定理，并对定理正确性进行证明；其次根据推导定理，提出了基于相同结构确定图极大团子图划分的不确定图极大团枚举算法D-MULE-D，并给出了其详细的算法描述；然后通过具体实例对D-MULE-D算法实现进行说明；随后通过实验分析，在不同阈值α下，对9个不同领域的数据集分别应用D-MULE-D算法和MULE算法，比较两种算法的运行时间；最后通过比较得出结论。

2. 问题定义

定义1 (确定图)：确定图通常用一个二元组G = (V, E)表示，其中V是图的顶点集合，顶点v∈V，E是图的边集合，E = { |v, w∈V}。其中 表示图中顶点v和顶点w是联通的。

定义2 (团)：给定确定图G = (V, E)，若存在顶点集合 $\text{C}\subseteq \text{V}$，且C中每一对顶点都存在边，那么称C是图G的一个团。

定义3 (极大团)：给定确定图G = (V, E)，若存在顶点集合 $\text{M}\subseteq \text{V}$，M为团，且不存在一个顶点 $\text{v}\notin \text{M}$，使得 $\text{M}\cup \text{v}$ 是图中的团，那么称M是图G中的一个极大团。

定义4 (不确定图)：不确定图通常用一个三元组G = (V, E, P)表示，其中V是图的顶点集合，顶点v∈V，E是图的边集合，边e∈E，P是边的权值集合，0 < p < 1，p∈P表示顶点间联通的概率。

定义5 (α团)：给定不确定图G = (V, E, P)和阈值α，0 < α < 1，若存在顶点集合 $\text{C}\subseteq \text{V}$，C中每一对顶点都存在边，且C的团概率大于等于α，那么称C是一个α团。其中C的团概率是指C中顶点对在图中对应的边的权值的乘积。

定义6 (α极大团)：给定不确定图G = (V, E, P)和阈值α，0 < α < 1，若存在顶点集合 $\text{M}\subseteq \text{V}$，M为α团，且不存在一个顶点 $\text{v}\notin \text{M}$，使得 $\text{M}\cup \text{v}$ 是图中的α团，那么称M是图G中的一个α极大团。

根据以上定义，我们可以将确定图中团和极大团的定义与不确定图中α团和α极大团的定义相结合，得出以下定理：

定理1：给定不确定图G = (V, E, P)和阈值α，0 < α < 1，其任意一个α团C必然是与其结构相同的确定图G’ = (V, E)的一个团。

定理证明

给定不确定图G = (V, E, P)和阈值α，0 < α < 1，则与其相同结构的确定图G’ = (V, E)。

对于G中的任意一个α团C，

∵C是G的α团；

∴根据定义5，C中的每一对顶点间都存在边；

∵G’与G结构相同，具有相同的顶点和边；

∴在G’中， $\text{C}\subseteq \text{V}$ 且C中的每一对顶点间都存在边；

∴根据定义2，C是G’的一个团。

定理2：给定不确定图G = (V, E, P)和阈值α，0 < α < 1，其任意一个α极大团M对于其结构相同的确定图G’ = (V, E)，在G’中必然存在一个极大团 ${\mathrm{M}}^{\prime }\supseteq \text{M}$。

定理证明

给定不确定图G = (V, E, P)和阈值α，0 < α < 1，与其相同结构的确定图G’ = (V, E)。

对于G中的任意一个α极大团M，

∵M是G的α 极大团；

∴根据定义6，M是G的α团；

∵G’与G结构相同，具有相同的顶点和边；

∴在G’中， $\text{M}\subseteq \text{V}$ 且M中的每一对顶点间都存在边；

∴根据定理2，M是G’的一个团；

∴根据定义3，在G’中必然存在一个极大团 ${\mathrm{M}}^{\prime }\supseteq \text{M}$。

3. 算法描述

根据上面推导的定理3，给定不确定图G = (V, E, P)和阈值α，0 < α < 1，其任意一个α极大团M对于其结构相同的确定图G’ = (V, E)，在G’中必然存在一个极大团 ${\mathrm{M}}^{\prime }\supseteq \text{M}$。因此，如果对不确定图先进行子图划分，先得到与其结构相同的确定图的极大团，再对不确定图中这些极大团子图应用MULE算法，从而枚举出不确定图的α极大团，将大幅提高不确定图极大团枚举效率，降低时间复杂度。

基于以上不确定图子图划分策略，我们提出了一种新的不确定图极大团枚举算法D-MULE-D，该算法先通过Degeneracy算法对不确定图进行子图划分，将不确定图按其相同结构的确定图划分成极大团子图集合，然后再对这些不确定图的极大团子图分别应用MULE算法，从而枚举出其不确定图的α极大团，再通过顶点规模降序过滤策略过滤掉伪α极大团，从而得到最终的α极大团集合。其中顶点规模降序过滤策略是将极大团集合根据其每个极大团内顶点个数进行降序排列，再顺序对顶点集合间进行判断，如果前者包含后者，说明后者为伪极大团，直接将伪极大团从极大团集合中删除，直到所有顶点集合间包含关系都判断完结束。该策略能够尽早发现伪极大团，通过剔除伪极大团，从而减少验证极大团的次数，提高验证效率。

4. 数据分析

根据以上对D-MULE-D算法的描述，下面我们以具体实例对算法的实现进行说明，对于给定不确定图G，如图1所示：

Figure 1. Uncertain graph G

图1. 不确定图G

设定α = 0.1，则对于不确定图G应用D-MULE-D算法，其算法实现如图2~4所示：

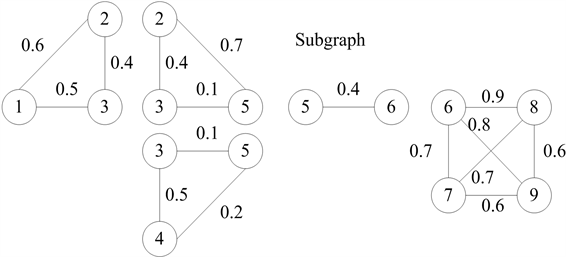
Figure 2. The subgraphs obtained by using Degeneracy algorithm

图2. 应用Degeneracy算法进行子图划分

Figure 3. The MULE algorithm is applied to subgraphs respectively

图3. 对子图分别应用MULE算法

Figure 4. The vertex size descending filtering strategy is applied

图4. 应用顶点规模降序过滤策略

5. 实验验证

实验使用的硬件平台是英特尔酷睿i7-8700K处理器，主频3.70 GHz，1TB HDD硬盘和8 GB DDR4内存，64位Windows 10操作系统；运行环境为Microsoft Visual Studio 2010；编程语言为C++。本文所使用的实验数据来源于9个不同领域的数据集，分别是Anthra、Mtbrv、Amaze、Kegg、Xmark、Nasa、Citeseer、Go和Yago数据集。对于阈值α = 0.2，0.4，0.6，0.8，分别应用MULE和D-MULE-D算法枚举极大团，两者的运行时间对比如图5~8所示。

Figure 5. The running time comparison between the MULE and D-MULE-D algorithm when α = 0.2

图5. α = 0.2时MULE和D-MULE-D算法枚举极大团运行时间对比

Figure 6. The running time comparison between the MULE and D-MULE-D algorithm when α = 0.4

图6. α = 0.4时MULE和D-MULE-D算法枚举极大团运行时间对比

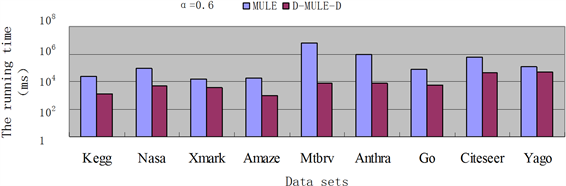
Figure 7. The running time comparison between the MULE and D-MULE-D algorithm when α = 0.6

图7. α = 0.6时MULE和D-MULE-D算法枚举极大团运行时间对比

Figure 8. The running time comparison between the MULE and D-MULE-D algorithm when α = 0.8

图8. α = 0.8时MULE和D-MULE-D算法枚举极大团运行时间对比

通过以上实验分析，我们可以发现对于大规模数据的不确定图，应用MULE算法的时间复杂度是O (n·2ⁿ)，而应用D-MULE-D算法的时间复杂度是O (n·3^n/3)，D-MULE-D算法的运行时间要明显低于MULE算法。同时，对于不同的阈值α，因MULE算法运行取决于顶点数量n，其运行时间变化不大；而由于阈值α的增大，α极大团会相应减少，α极大团内顶点个数也会减少，从而检验极大性检验次数也会减少，因此D-MULE-D算法的运行时间会随着阈值α的增大而减少。

6. 结论

本文通过对不确定图极大团枚举算法MULE进行研究，并结合确定图与不确定图在结构相同时极大团的相互关系，提出了一种新的不确定图极大团枚举算法D-MULE-D，该算法通过对不确定图进行极大团子图划分，再对极大团子图应用MULE算法枚举α极大团，随后对α极大团集合按照顶点规模倒序排列检验其极大团的正确性，尽早过滤掉其中的伪α极大团，从而得到最终正确的α极大团集合。通过实验分析，D-MULE-D算法的运行时间要明显低于MULE算法，并且对于不同的阈值α，D-MULE-D算法的运行时间会随着阈值α的增大而减少。因此，D-MULE-D算法的运行效率要明显高于MULE算法。