基于时间序列分析的福建省GDP预测研究

Forecast and Research on GDP of Fujian Province Based on Time Series Analysis

摘要: 首先基于时间序列分析原理，通过Eviews软件对福建省1978~2015年的GDP数据进行拟合分析，建立了ARIMA(4,2,2)和ARIMA(4,3,2)模型。然后应用两模型对福建省2016~2018年的GDP进行检验，发现ARIMA(4,3,2)模型的预测误差较小，所以认为该模型拟合效果较好。最后应用ARIMA(4,3,2)模型对福建省2019~2023年的GDP进行预测。

Abstract: Firstly, based on the time series analysis theory, the GDP of Fujian province from 1978 to 2015 was fitted and analyzed by Eviews software; the ARIMA(4,2,2) model and ARIMA(4,3,2) model were established. Secondly, using the two models, the GDP of Fujian province in 2016~2018 was used to test. We found the prediction error of ARIMA(4,3,2) is smaller, so it is considered that the model has a good effect. Finally using ARIMA(4,3,2) model, the GDP of Fujian province in 2019~2023 was predicted.

1. 引言

福建省是我国沿海经济带及海峡西岸经济区的重要省份，近些年随着“一带一路”等政策的逐步实施，经济得到持续提升，但是福建省经济水平和其他先进省份相比还是存在一些差距的。因此对福建省GDP的趋势做出预测，将有助于政府对未来做出更好的决策，这将有益于政府对宏观经济的调控，从而使宏观经济得到良好的发展 [1]。目前GDP的预测模型主要有多元回归模型、生产函数模型、灰色理论模型、人工神经网络模型、时间序列模型等 [2]。其中时间序列模型较为常用，近年来我国也有许多应用时间序列模型对GDP进行预测研究的例子 [3] [4] [5]。常用的时间序列模型包括自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型、求和自回归移动平均(ARIMA)模型 [6]。本文主要使用时间序列模型中的ARIMA模型，通过Eviews软件，结合1978~2015年福建省GDP数据建立时间序列模型，并应用建立的模型对2016~2018年的福建省GDP数据进行预测，通过对比预测值与真实值的差值计算出相对误差，从而来考量模型预测的准确性，选择较准确的ARIMA模型对福建省未来GDP进行预测。

2. 数据收集

为了分析和预测福建省GDP，我们在福建省统计局官网的统计年鉴收集到了1978~2018年的福建省GDP数据 [7]，如表1。

Table 1. GDP of Fujian province from 1978 to 2018

表1. 1978~2018年福建省GDP

3. ARIMA(4,2,2)模型的建立

3.1. 平稳性检验

用Excel绘制出福建省1978~2015年的GDP时序图，如图1。

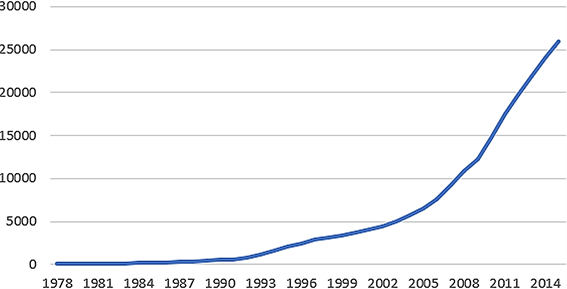
Figure 1. Sequence diagram of Fujian province’s GDP from 1978~2015

图1. 福建省1978~2015年GDP时序图

由时序图可以看出，大概从2002年开始，福建省GDP增长速度较快，从总体趋势来看，该时间序列呈明显的上升趋势，因此可认为该时间序列为非平稳序列。接下来的模型建立过程中，我们可以通过单位根检验的方法进一步对序列的平稳性进行检验，在Eviews中将福建省GDP的时间序列命名为{X}并进行平稳性检验，得到检验结果如图2。

由运行结果可知，显著水平为10%的t统计量值为−3.215267，而时间序列{X}的t值为1.419408，大于显著水平10%下的t值，所以不能拒绝原假设，序列存在单位根，即该时间序列是非平稳的。为了使非平稳序列变为平稳序列，我们应对其进行差分，但由于原始序列呈指数增长趋势，所以我们首先要对原始序列取对数，来消除可能存在的异方差问题。将取对数后的序列{LNX}进行ADF检验，结果如图3。

Figure 2. Unit root test of {X}

图2. {X}的单位根检验

Figure 3. Unit root test of {LNX}

图3. {LNX}的单位根检验

由运行结果可知，取对数后的时间序列依然不平稳，因此我们应再对其进行一阶差分，得到序列{D(LNX)}，其单位根检验结果如图4。由运行结果可知，一阶差分后显著水平为10%时的t统计量值为−3.215267，而时间序列{D(LNGX)}的t值为−2.289593，大于−3.215267，所以不能拒绝原假设，该时间序列依然是非平稳的，所以接下来我们要继续对序列进行二阶差分，得到序列{D(LNX,2)}，其单位根检验结果如图5。

由运行结果可知，二阶差分后时间序列{D(LNX,2)}的t统计量值−7.130786小于显著水平1%的临界值−4.252879，所以不存在单位根，即序列平稳。

Figure 4. Unit root test of {D(LNX)}

图4. {D(LNX)}的单位根检验

Figure 5. Unit root test of {D(LNX,2)}

图5. {D(LNX,2)}的单位根检验

3.2. 模型识别

二阶差分后的时间序列{D(LNX,2)}已经平稳，接下来我们将通过自相关图和偏自相关图来对模型进行识别，选取合适的模型并判断p,q的取值。使用Eviews绘制出序列的自相关图和偏自相关图如图6。

Figure 6. Autocorrelation diagram and partial correlation diagram of {D(LNX,2)}

图6. {D(LNX,2)}的自相关图和偏自相关图

时间序列{D(LNX,2)}的自相关图系数在k = 2以后进入二倍标准差内，偏自相关图系数在k = 4后进入二倍标准差内，且进入二倍标准差内的自相关系数和偏自相关图系数没有快速趋于0，还存在着较大的波动数值，所以认为该序列的自相关系数和偏自相关系数均为拖尾，可以尝试建立p < 4，q < 2的ARIMA(p,2,q)模型，选择符合条件的最优模型进行预测。

3.3. 参数估计

经过尝试发现，只有ARIMA(4,2,2)模型通过了检验，所以这里以ARIMA(4,2,2)模型的建模过程为例。在Eviews的运行结果中，AR(1)和AR(3)的Prob(伴随概率)值分别为0.1287和0.6662，均大于0.05，故没有通过t检验，参数不显著。剔除不显著的项再进行估计，结果发现MA(1)项的伴随概率为0.5855大于0.05，还是没有通过t检验，将其剔除再次进行估计，最终结果如图7。

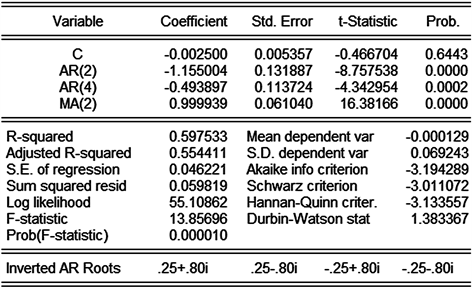
Figure 7. Modeling result of ARIMA(4,2,2) after the AR(1), AR(3), MA(1) are eliminated

图7. ARIMA(4,2,2)剔除AR(1)、AR(3)、MA(1)项的建模结果

此时Prob值均小于0.05，参数显著，且根均在在单位圆内，所以可以建立该模型，模型方程为：

$x_t=-0.0025-1.155004x_{t-2}-0.493897x_{t-4}+{\epsilon }_t-0.999939{\epsilon }_{t-2}$

3.4. 模型检验

接下来对建立的模型进行白噪声检验，检验模型的适应性。判断方法有两种，一种是观察自相关图的系数是否在二倍标准差内，如果是则为白噪声；另外一种是看伴随概率是否大于0.005，如果均大于0.005则为白噪声。在Eviews中进行白噪声检验，结果如图8。

ARIMA(4,2,2)模型残差的自相关系数均在二倍标准差内，P值也均大于0.005，所以可以认为序列之间没有任何关联，即为白噪声序列，可以用该模型进行预测。

4. ARIMA(4,3,2)模型的建立

4.1. 平稳性检验

之前我们对取对数后的时间序列{LNX}进行了二阶差分并建立了模型，现在我们来尝试进行三阶差分并建模，对比二阶差分和三阶差分的效果，选出预测效果最好的模型。在Eviews中对取对数后的时间序列{LNX}进行三阶差分得到序列{D(LNX,3)}，进行单位根检验，结果如图9。

Figure 8. Residual correlation diagram of ARIMA(4,2,2) model

图8. ARIMA(4,2,2)模型的残差相关图

Figure 9. Unit root test of {D(LNX,3)}

图9. {D(LNX,3)}的单位根检验

由单位根检验结果可知，三阶差分后序列{D(LNX,3)}的t统计量值为−4.928516小于显著水平为1%的临界值−4.284580，所以不存在单位根，该序列平稳。

4.2. 模型识别

在Eviews中做三阶差分的自相关图和偏自相关图如图10。时间序列{D(LNX,3)}的自相关图系数在k = 5以后进入二倍标准差内，偏自相关图系数在k = 4后进入二倍标准差内，且进入二倍标准差内的自相关系数和偏自相关图系数没有快速趋于0，还存在着较大的波动数值，所以认为该序列的自相关系数和偏自相关系数均为拖尾，可以尝试建立p < 4，q < 5的几个ARIMA(p,3,q)模型，选出通过检验的最优模型。

4.3. 参数估计

经过尝试，只有ARIMA(4,3,2)模型通过了检验，所以这里以建立ARIMA(4,3,2)模型为例进行操作。在Eviews的几次运行结果中，AR(1)、AR(3)和MA(1)的伴随概率均大于0.05，没有通过t检验，参数不显著，剔除不显著项重新估计，最终得到结果如图11。

此时伴随概率均小于0.05，参数显著且根均在单位圆内，所以该模型可建模，模型方程为：

$x_t=0.004544-1.272193x_{t-2}-0.605696x_{t-4}+{\epsilon }_t-0.999971{\epsilon }_{t-2}$

4.4. 模型检验

利用Eviews对ARIMA(4,3,2)模型进行白噪声检验，结果如图12。

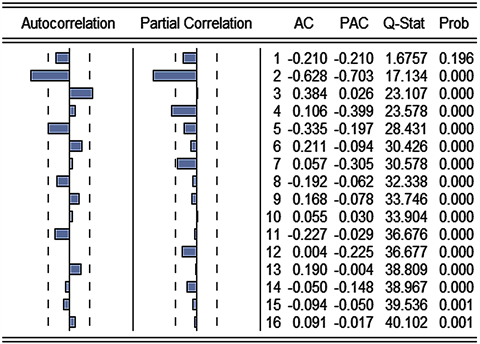
Figure 10. Autocorrelation diagram and partial correlation diagram of {D(LNX,3)}

图10. {D(LNX,3)}的自相关图和偏自相关图

Figure 11. Modeling result of ARIMA(4,3,2) after the AR(1), AR(3), MA(1) are eliminated

图11. ARIMA(4,3,2)剔除AR(1)、AR(3)、MA(1)项的建模结果

ARIMA(4,3,2)模型残差的自相关系数均在二倍标准差内，P值也均大于0.005，所以可以认为该模型序列之间没有任何关联，即为白噪声序列，所以可以用于预测。

5. 预测结果检验

利用Eviews对福建省2016~2018年的GDP进行预测，得到预测值，但此时预测后的结果是取对数后的预测值，我们需要将其还原为原序列值的形式，还原后得到的数据如表2。

通过对比可以发现，ARIMA(4,3,2)模型的平均相对误差更小，预测效果更好，所以应选择ARIMA(4,3,2)模型进行预测，得到福建省GDP预测值如表3。

预测出 2019~2023年的GDP值分别为39,077.03亿元、44,903.9亿元、52,959.35亿元、63,306.92亿元、78,094.12亿元。

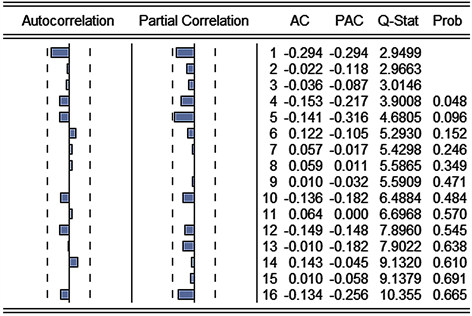
Figure 12. Residual correlation diagram of ARIMA(4,3,2) model

图12. ARIMA(4,3,2)模型的残差相关图

Table 2. Comparison of model results

表2. 模型结果比较

Table 3. GDP forecast of Fujian province

表3. 福建省GDP预测

6. 总结与展望

本文在对福建省GDP进行预测研究过程中，首先阐述了研究现状和研究方法，并介绍了研究思路和运用的几种模型。然后在福建省统计局官网上收集到了福建省的GDP数据，运用Eviews软件，基于时间序列分析原理对数据进行了平稳性检验、模型识别、参数估计、白噪声检验等一系列处理，最终建立了ARIMA(4,2,2)及ARIMA(4,3,2)两个模型，分别用它们进行预测，并对比预测结果，计算出预测误差，最终发现ARIMA(4,3,2)模型的预测效果相对于ARIMA(4,2,2)较好，所以确定ARIMA(4,3,2)是最优模型，可以对福建省未来GDP进行有效预测。

在经济全球化的今天，某个国家或地区的经济情况很容易受到自然灾害或国际形势等突发情况的影响，面对这些情况需要具体问题具体分析，预测的准确程度难免会有所降低。此外，ARIMA模型也只在短期预测中较为精确，并不适用于长期预测。即便如此，我们仍然可以使用ARIMA模型进行粗略预测，判断出未来短期内的经济走势，对已存在的问题作出适当调整，对将来有可能发生的问题做好准备，这将会有利于政府经济计划的改良并促进经济发展。