大雷诺数下串列方柱的PIV试验研究

PIV Experimental Investigation of Series Parallel Column with High Reynolds Number

摘要: 为了研究机械结构以及建筑物周围的流场特性，减小工程设计不当造成的损失。采用粒子图像测速设备PIV，对不同间距下的串列方柱，分别进行雷诺数为6.8 × 103、1.4 × 104、2.2 × 104、3.42 × 104的方柱绕流风洞实验，研究了串列方柱在大雷诺数下，方柱非定常绕流的流场特征和斯特罗哈数的变化特性。结果表明，在大雷诺数下，PIV试验能清晰观察到下游方柱的非定常流场特征，时均流场中距离方柱2倍间距以及瞬时流场中距离方柱3.5间距的范围内，受到上游方柱干扰较大，在小于3.5倍间距时，工程中应考虑上游的干扰，进行合理结构设计；下游方柱斯特罗哈数接近于常值0.12；在流体机械及建筑工程中结构的设计有着重要指导意义。

Abstract: In order to study the mechanical structure and the characteristics of the flow field around the building to reduce the loss caused by improper engineering design. Particle Image Velocimetry (PIV) was used, under different working conditions in tandem column. The wind tunnel experiments with Reynolds numbers of 6.8 × 103, 1.4 × 104, 2.2 × 104 and 3.42 × 104 were carried out. The flow field characteristics and St characteristic of unsteady flow around the square column under large Reynolds number are studied. The results demonstrate that under the large Reynolds number, the unsteady flow field characteristics of the downstream square column can be clearly observed in the PIV test. The time-averaged flow field in the distance from the square column 2D and instantaneous flow field in the range of 3.5D from the square column, the interference from the upper side column is larger. In less than 3.5D, when the project should consider the upstream interference, a reasonable structural design. The downstream column St is on the brink of a constant value of 0.12. In fluid machinery and construction design of the structure has important guiding significance.

1. 引言

方柱绕流现象广泛存在于桥梁工程、海洋工程、水电工程和流体机械等工程科学领域中，例如石油开采平台的墩柱、港口码头的桩柱、电厂的冷却塔等都存在着串列方柱结构。若处于流体快速流动的环境中，会出现旋涡分离、脱落等复杂流动现象，方柱通常由于旋涡脱落而产生振动，当振动频率接近方柱固有频率时就会引起共振，从而导致机械结构损坏、建筑物坍塌等灾难性事故。全面性地研究串列方柱，并观察周围真实的流场特性对人们解决结构设计等相关实践工程中的问题具有重要意义。

在圆柱和方柱等钝体绕流方面，国内外许多学者都进行了长时间的研究。Lyn等 [1] 率先采用LDV (laserdoppler velocimetry)给出了雷诺数为2.2 × 10⁴时单点试验结果；Durão给出了雷诺数为1.4 × 10⁴的单点试验结果 [2]，目前很多关于流体方面的动力学数值模型以及计算方法均使用他们的试验结果作为校核的基本标准。许多学者在尾流的涡脱落特性和涡致振动上也进行了研究 [3] [4] [5]；Kim和Lee等 [6] 采用热线风速仪和PIV (particle image velocimetry)技术获得在Re = 2.2 × 10⁴时单方柱绕流的斯特劳哈尔数为0.136和时均流场。研究中也发现计算域壁面和雷诺数对方柱有一定的影响 [7] [8]。在多个钝体中，周云龙 [9] 研究了双相流并列方柱的涡脱落特性；而Sohankar [10]、陈素琴 [11]、吴七二 [12]、吕启兵 [13] 等学者通过数值模拟对不同间距比下串列双方柱的绕流特征进行了分析；Liu和Chen [14] 实验研究了间距从1.5到9.0，雷诺数从2.0 × 10³到1.6 × 10⁴的情况下串列方柱的流动特性。从上述可以看出，在串列方柱方面，缺乏大雷诺数工况下，下游方柱流场受干扰时的流动特性以及流场空间结构研究。

鉴于此，本文主要应用PIV粒子图像测速仪对大雷诺数下背风向方柱的非定常绕流进行风洞试验，研究了尾流中流场受干扰时的流动特性。最后总结出斯特罗哈数与雷诺数及间隙比的关系曲线，对一些流体机械及建筑物的结构设计有着重要的意义。

2. IV试验布置

串列方柱绕流的PIV试验是在西华大学流体及动力机械教育部重点实验室的XHWT-1风洞中进行。该风洞为回流式风洞，风洞的截面尺寸为宽1.2 m，高1.2 m，试验段长3 m，风洞试验的风速范围在0~60 m/s。

流场测试装备选用美国TSI公司三维PIV粒子图像测速系统，系统中的激光器可以产生532nm波长的单一激光，单脉冲的最大能量为132 mJ，其最高频率为30 Hz，激光器产生绿色的激光照亮测试添加了示踪粒子的区域。风洞中安装的有发烟装置，试验过程中均采用烟线法，示踪粒子直径小，不会影响流场；在同步器保证激光产生时间与双CCD相机成像同步的情况下，能通过双CCD相机快速成像，瞬间“冻结”住流场，利用专业软件Tecplot等，通过互相关算法运算，得到在间隔时间内测试区域中大量示踪粒子的位移，从而获得流场中一个平面内的多点流场特性等。方柱的风洞实验台布置如图1。

Figure 1. Arrangement of wind tunnel test-bed

图1. 风洞实验台布置

串列方柱绕流试验示意图如图2。两个方柱模型均为光滑木质材料，尺寸为长100 cm，宽5 cm，宽5 cm，方柱表面对激光有部分反射。方柱宽为D，下游方柱中线距风洞试验段最左侧为30D，距最右侧为30D，试验整个过程都固定不动，上游方柱距离下游方柱为L。通过移动前方柱来改变两个方柱的间距，间距的改变会导致后方柱下游的流场特征也可能产生变化。间距比定义为G = L/D，串列方柱间距为5 cm、10 cm、20 cm、30 cm以及40 cm的间隙比分别是1、2、4、6、8。雷诺数Re = ρU₀D/v，其中U₀为来流风速，v表示运动粘性系数。试验在均匀流条件下，紊流度小于0.5%，风速分别为2 m/s、4.1 m/s、6.4 m/s和10 m/s。

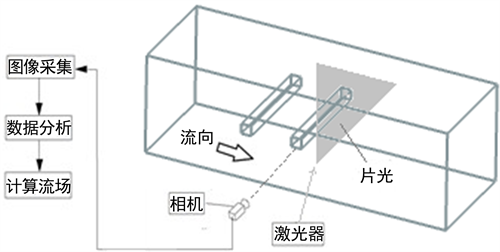
Figure 2. Schematic diagram of the flow around a square column

图2. 串列方柱绕流试验示意图

3. 实验结果及分析

实验观测到串列方柱在不同雷诺数和间距(比)工况时，下游方柱绕流流动过程。通过方柱绕流的二维流动特性和PIV测速仪的特性，对下游方柱中间水平面进行实验观测，同步器采集间隔时间最小为190 ns，采样频率为15 Hz，单租共采样840对图片。

对下游方柱在不同工况下，尾流中的时均流场流动特性以及瞬时流场的旋涡产生、脱落及发展等交替演化动态过程进行观测分析，得到了瞬时流场图、时均流场图，并比较了两种流场的结构特性；同时分析后方柱侧面和下游的时均速度特性。

3.1. 下游方柱中间断面的时均流速流动特性分析

图3是下游方柱在不同雷诺数和间距工况下的水平时均流速曲线图， $G=\infty$ 代表的是单方柱的无干扰流场特性。由图3(a)~(d) 4幅图可以观察到，同一雷诺数下，当串列方柱的间距比G ≤ 4.0时，随着间距比的增大，水平时均流速呈下降趋势，这是由于在小间距时，上游方柱尾流还未形成涡街，上游方柱高速分离的剪切层流附着在下游方柱两边面上，下游方柱尾部流速就受到一个推进的作用，故下游方柱尾部速度能较快接近风速，时均流速比也就相对较高，而随着间距的增大，上游方柱尾流逐渐开始形成半涡街状态，产生涡区并流动激烈，旋涡干扰到下游方柱的尾部流场，导致时均流速比相对较低；当间距比G > 4.0时，从图中能够看出G = 6和8的趋势与单方柱的差距不大，但是仍存在一定的影响，这是由于间距增大后，前后方柱尾部都形成涡街，距离越远，前方柱对后方柱的影响就越小，趋势也就越接近单方柱，最后都稳定在0.6左右，与Durão的实验结果趋势相吻合。

(a) Re = 6.8 × 10³ (b) Re = 1.4 × 10⁴ (c) Re = 2.2 × 10⁴ 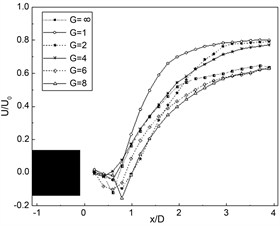(d) Re = 3.42 × 10⁴

Figure 3. Horizontal velocity profile

图3. 水平速度剖面

从图中可以观察到串列方柱在间距比大于或小于4.0时的时均流速存在较明显的区别。临界间距被定义为当L/D为一定值时，流场会有两种不同的形态，并且大于这一定值时的流动形态和小于这一定值的流动形态截然不同 [15]。因此可以得到本试验串列方柱的临界间距在G = 4.0附近。同时，得到在同一间隙比下，随着雷诺数的增大，时均流速也逐渐升高。总体看来，各工况下，在x/D < 3时，时均速度较大；而在x/D=3时，较远区域速度略小，流速逐渐都趋于稳定。

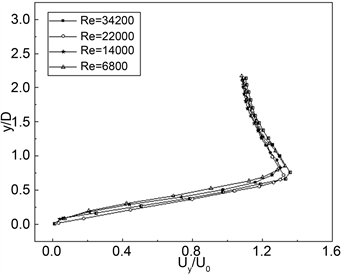
图4给出了G = 4和G = 6时，后方柱竖向时中线均速度曲线图，图中可以了解到本文试验检测到的风速偏小，从图4(a)、图4(b)中可以观察到不同雷诺数不同间距下方柱侧面的时均流速趋势一致，图4(b)中加入单方柱试验作比较，趋势大致相同，而在时均流速的拐角点与稳定流速上，单方柱试验与串列方柱试验存在一定的区别，这是由于串列方柱中后方柱受到前方柱所形成的涡区的影响，干扰到侧面的流场，导致达到时均流速最大值和稳定流速也就相对距离方柱侧面较远，整体差别不大。由于实验条件的限制，近壁拍摄效果不佳，以致于方柱壁面流动状态在试验中没有检测到好的效果。

(a) G = 4.0 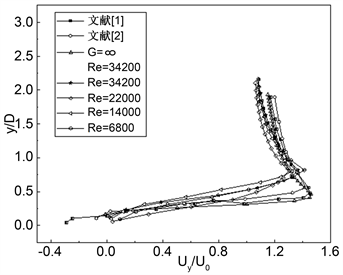(b) G = 6.0

Figure 4. Vertical velocity profile

图4. 竖向速度剖面

3.2. 下游方柱绕流瞬时流场分析

图5中图5(a)是在G = 1.0，Re = 6.8 × 10³工况下时的瞬时流场，方柱尾部下方形成了明显的旋涡，旋涡直径与方柱特征长度差不多大，旋涡逐渐脱落完成后，延顺风向逐渐发展和扩散到远处，紧接着在方柱上方也逐步形成漩涡并完成脱落，旋涡总是不断交替产生的，然后发展和扩散大约在距方柱约3D的位置，流场受旋涡的影响也慢慢减小，流线也逐渐趋于平稳。

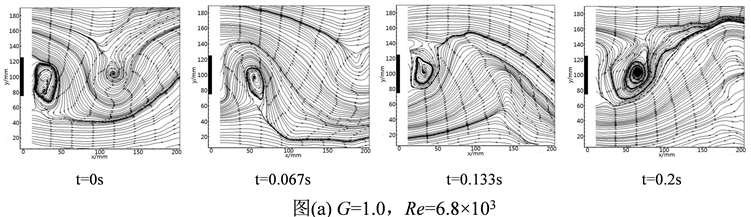
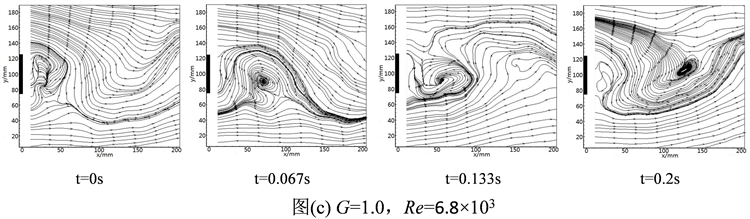
Figure 5. Transient flow field under different clearance ratio and Reynolds number

图5. 不同间隙比和雷诺数工况下的瞬时流场图

图5(b)与图5(a)是在同一间距下，增大雷诺数的瞬时流场图，将不同时刻下的流场进行比较得到，随着雷诺数的增大，旋涡的形成和脱落频率增大，涡波动的幅度也逐渐增大，旋涡对流场的影响也越远，在距离方柱3.5D的地方存在涡的扰动。

图5(c)与图5(a)是在同一雷诺数下，不同间距比的瞬时流场图，两组图片互相对比可以得到，随着间距比的增大，形成的旋涡在同一时刻下对流场的干扰扩大，流动幅度波动也较大，同时整个流场也受到影响，变得不均匀。

3.3. 下游方柱绕流时均流场分析

同间距，不同雷诺数的各工况下，从时均流场图6可以看出，由于流体速度的改变，方柱两边的压力大于方柱尾部的压力，形成了压差，随着雷诺数的增大，尾流区逐渐开始形成旋涡，产生的两个旋涡，旋转方向相反，大小大致相等。此后在尾流区末尾处两个旋涡将交汇于一点，然后向下游流动，并随着距离方柱越远，旋涡的干扰也逐步减小，尾流区后面部分的流线从弯曲逐渐趋于水平。对于同雷诺数，不同间距的工况下，随着间距的逐渐增大，尾流区也慢慢开始形成漩涡，特征一样。总体上我们可以观察到时均流场都是趋于对称结构的，不完全对称是由于实验采集的数据量不够导致。

图7是在临界间距G = 4.0时方柱侧面的时均流场图，可以看出随着雷诺数的增大，对方柱侧面的流场影响并不大，由于近壁拍摄效果不佳，所以根据采样的区域可以推算出，下游方柱在约0.7D的范围内有一定的影响，这与上述侧面的时均流速曲线相符合。

图8是各工况下时均流场中汇流点长度变化曲线图，h表示汇流点到方柱的距离。从图中可以观察出，串列方柱同雷诺数下，后方柱下游的尾流区长度随间距的增大而增大；而在同一间距的工况下，汇流点的长度会随雷诺数的增大而逐步减小。整体上流量的增大对回流区的长度影响较小，回流区长度都在约一倍D的距离波动。

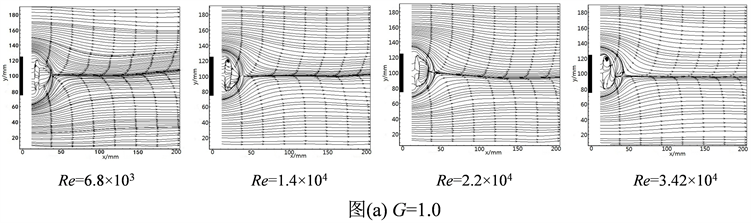
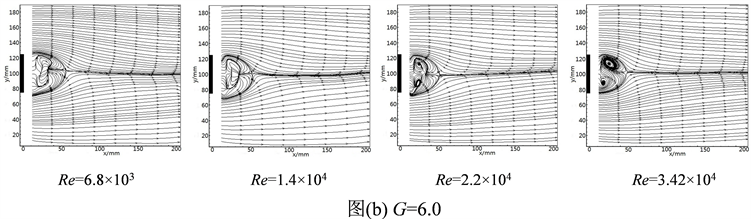
Figure 6. Time-averaged flow fields of different Reynolds number and gap ratio downstream

图6. 不同雷诺数和间隙比下方柱下游的时均流场图

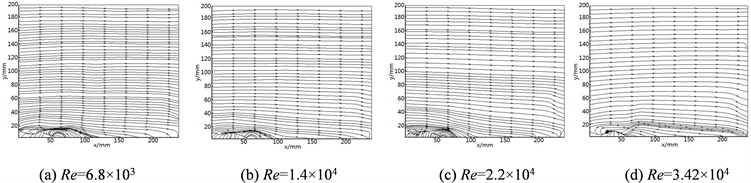
Figure 7. G = 4.0, Time-averaged flow field of the side column under different Reynolds numbers

图7. G = 4.0，不同雷诺数下方柱侧面的时均流场图

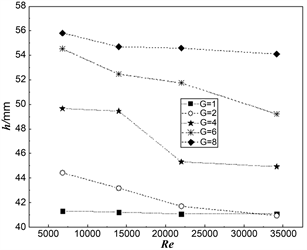
Figure 8. Relationship between length of confluence under different Reynolds numbers and different clearance ratios

图8. 不同间隙比、不同雷诺数下与汇流长度的关系

3.4. 瞬时流场与时均流场的比较

大雷诺数下，时均流场中的方柱会在下游逐渐形成两个大小相等，方向相反的旋涡，并且有一个较明显的汇流点，流场远处趋于水平，整个流场都处于比较对称的状态，而且能够较快得到流场的一个平均流速，找出与理论流速的误差。从图中可以看出时均曲线在距离方柱约2D的地方接近水平，大于2D时流场比较均匀，而在小于2D的范围内，流场受干扰严重。

对于瞬时流场，方柱下游的旋涡交替出现，不断向远处移动，流场随时间在不断地变化，每个位置的特性不同，却能最能反映出流场真实的非定常流动特性。但是瞬时流场中在距离方柱3.5D的范围内流场流动剧烈。两者流场各有优势，实际工程设计时，小于3.5D时要考虑上游柱体对下游的影响。

3.5. 不同间距比时旋涡脱落St与Re的关系

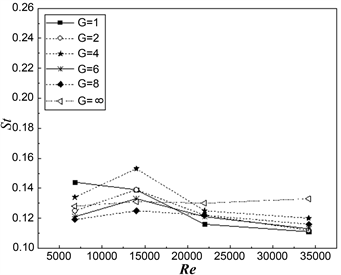
St在圆柱、方柱等钝体绕流研究领域中有着重要的作用，其表达公式为：St = fD/U₀ (f表示涡脱落频率)。图9是在几种间隙比的工况下，Re分别为6.8 × 10³、1.4 × 10⁴、2.2 × 10⁴、3.42 × 10⁴时的St数。

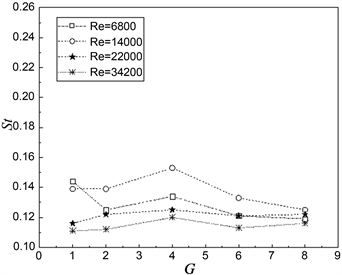(a) (b)

Figure 9. The relationship between Reynolds number and St of different clearance ratio

图9. 不同雷诺数、间距比与St的变化关系

从图9(a)可以看出， $G=\infty$ 是表示单方柱的St曲线，St随Re的不断变化并接近于常值0.13；而串列方柱的下游方柱St是在0.11~0.16的范围内变化。雷诺数较小时，St波动规律不明显；随着雷诺数的逐渐增大，St慢慢减小并最终趋于稳定并接近常值约0.12，比单方柱的St略小。可以理解为串列方柱间的风速小于无穷远处的风速，所以后方柱的涡脱落频率相对于单方柱要小，则St比单方柱的略偏小。从图9(b)中我们可以得到，在同一雷诺数下，G ≤ 4.0时，St随间距的增大而缓慢增大；而G > 4.0时，St随间距的增大逐渐减小。

4. 结论

1) 通过PIV风洞试验，观察到大雷诺数下，上游方柱对下游方柱周围非定常流场的干扰特征，时均流场中在距离方柱小于2D时受影响较大，相比单方柱的流场更加剧烈，大于2D则干扰较小。而瞬时流场在小于约3.5D的范围内影响较大。在小于3.5D的条件下，流体机械或者建筑结构工程中不应忽略上游方柱的干扰。

2) G ≤ 4时，下游方柱的水平时均流速随间距的增大而减小；当G > 4时，时均流速特性与单方柱趋于一致。时均流速随着Re的增大也逐渐增大。

侧面时均流速在不同工况下大致相同，在时均流速曲线的拐角点上，由于串列方柱间的涡区影响，与单方柱有一定的区别。

3) 方柱下游回流区的长度随间距的增大逐渐增大，随雷诺数的增大而逐渐减小，整体上接近于方柱的特征长度。

4) 小于临界间距时，St随间距增大而缓慢增大；大于临界间距时，St随间距增大而逐渐减小。St随雷诺数增大介于0.11~0.16之间变化，最终接近于常值0.12，相对单方柱的St略小。

基金项目

流体及动力机械教育部重点实验室开放基金(NO. szjj2014-045)；四川省科技厅项目(NO. 2016JY0187)。

NOTES

^*通讯作者。