1. 引言
设G是一个n阶图,G的邻接矩阵的特征值的全体构成G的谱。图的谱在分子轨道、量子化学和电子工程等领域内有着广泛的应用,其研究是代数图论的一项重要内容,其成果已经形成多部专著。在图的谱中正特征根的个数、负特征根的个数和零特征根的个数分别称为G的正惯性指数、负惯性指数和零度 [1] [2],并分别记作
、
、
。易知
;G的秩代表着非零特征根的个数;正特征根与负特征根的个数之差称为G的符号差。在化学中,用图可以表示一个共轭烃分子,称其为该分子的分子图。分子图的零度(或秩)在化学中有许多重要的应用。例如,一个分子化学性质的稳定性的一个满足条件之一就是其图的零度等于零。在1957年,Collatz和Sinogowitz在文献 [3] 中首次引入刻画所有奇异图的问题,这个问题引起了很多数学家和化学家的兴趣。在数学中,由著名的Graham-Pollak定理 [4] 知,图的负惯性指数不大于图的完全二部图分解数。因此,图的惯性在图的二部分解和星分解方面有很多应用。许多图论学者对各类图的正负惯性指数和零度做过大量的研究 [5] - [11],并取得出了很多结论。文献 [2] 讨论了树、单圈图、双圈图的正负惯性指数和零度,并给出了它们的计算方法,与此同时作者首次提出了图符号差的猜想。文献 [10] [11] 对于三类三圈图的正负惯性指数和零度进行了研究,并验证了关于图的符号差猜想对这三类图成立。本文讨论了另一类结构相对复杂的三圈图(即
)的正负惯性指数和零度,并给出了计算这类三圈图的正负惯性指数和零度的方法,此外检验了这类三圈图对于图的符号差猜想是成立的。
文章中出现的图都是简单无向图。设
是n阶图,
表示
图G的顶点集,
是图G的边集。设W是图G的一个非空点子集,用
表示由点子集W导出的子图,用
表示从G中删去W中的点以及与W中的点相关联的所有边后得到的图。用
表示两个顶点集不相交,称边数等于顶点数加上—1(0, 1, 2)的连通图为树(单圈图,双圈图,三圈图)。
三条内部不相交的路
的两个端点分别黏结成两个点后得到的图叫
-图,记为
,这里的
,且最多有一个等于2。由一条长为
的路两端上分别黏结图
的一个3度点和一个圈
上的一个点构成的图称为
-图,记作
(如图1),这里的
。根据所含的圈的类型,三圈图可分为15类,
= {所有只包含一个
—图作为导出子图的三圈图}是其中的一类。对于给定的三圈图
,将G的导出子图
-图称作图G的核,记作
。
2. 若干引理
引理1 [2] 若图
,其中
是图G的连通分支。则

Figure 1. Tricyclic graphs
图1. 三圈图
引理2 [2] 设图G中包含一条4个内点的度均为2的长为5的路,将用一条边来替换图G的这条路后得到的图记为H,则
引理3 [4] 设T是一棵阶数为n的树,那么
其中,
为树T的匹配数(即T的最大独立边数)。
设T是一棵树,
,如果存在树T的一个极大匹配不覆盖点v,则称点v为树T的一个未匹配点;否则,称v为树T的一个匹配点。若树T仅由一个点组成,约定该点是T的未匹配点。
设图
和n阶图
不相交,
,在
中把点u和
的任意k个点连接后得到的图称为
和
的关于点u的一个k-连图(
),记为
。由定义易知,当
时,图
不唯一。
引理4 [2] 设G为n阶图,树T含有一个可匹配点u,则对每一个正整数
有:
引理5 [2] 设G为n阶图,树T含有一个不可匹配点u,则对每一个正整数
有
引理6 [2] 设图G的每个分支是树,单圈图或是双圈图,则
并且在文献 [2] 中,作者提出了下面的猜想:
猜想:设G是一个图,则
引理7:设
,且
,
,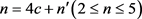 ,
,
,则
,
,
,则
证明:根据引理2,压缩三圈图
的内部路即得。
3. 主要结果
对于点数相对少的
-图
(不妨设
,其中最多有一个等于2,
),我们利用Matlab软件可计算出它的正负惯性指数和零度(见表1) (此处将图
均简记为G,
,
,
分别简记为p,n,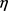 )。
)。



Table 1. Positive and negative inertia indexes and nullity of tricyclic graph ψ ( l , m , n , q , r ) ( 2 ≤ l , q ≤ 5, 3 ≤ m , n , r ≤ 6, l ≤ m ≤ n )
表1. 三圈图
的正负惯性指数和零度(2 ≤ l , q ≤ 5, 3 ≤ m , n , r ≤ 6, l ≤ m ≤ n)
设
-型的三圈图G (即
),三圈图G的核表示为
,对每一个点
,记
为包含点v且不包含
上的其他点的图G的最大连通导出子图,易知
是一棵树,假如存在点
使得点v是
的匹配点,则称图G是I—型的,否则称图G是II—型的。
定理1:设三圈图
,其中
为图G的核。
1)若G为I-型的,且点v是
的一个可匹配点则
其中
是树,
是一些双圈图,单圈图和树的并。
2) 若图G为II-型的,则
证明:1) 若G是I-型的,点v是
的可匹配点,则存在一个正整数
使得
成立,由引理4知
其中
是树,
是双圈图,单圈图和树的并。
2) 若G是II-型且G不是
-图,所以H有悬挂点或树,点v为
的未匹配点,由引理5有
反复运用引理1和引理5有
从而结论得证。
文献 [2] 中作者提出了一个猜想:设G是一个图,则
接下来的推论验证次猜想对本文所研究的一类三圈图成立。
推论1:设三圈图
,则
证明:设
是三圈图G的核,
1) 若G是I-型的且点v是
的匹配点,则
其中
是树,
是双圈图,单圈图和树的并,由引理6知对于树和双圈图,单圈图和树的并成立,从而对于三圈图G结论成立。
2) 若G为II-型的,由定理1知
因为
是森林,根据树的正负惯性指数相等,得
等于它的核的正负惯性指数之差,由引理7和表1中所含图的正负惯性指数之差,可检验
满足结论中的不等式,从而推论成立。
4. 结束语
本文受文献 [2]、文献 [10] 和文献 [11] 研究思路的启发,在15类三圈图中选取了结构相对复杂的一类(即
),讨论了其正负惯性指数和零度。详细数据可在本文给出的表格中查询(即表1)。最后在前人研究的基础上,验证了图的符号差猜想对于本文所研究的这类三圈图也成立。
基金项目
国家自然科学基金(11561056, 11661066),青海省自然科学基金(2016-ZJ-914)资助。