某些“积不出”函数的定积分近似计算方法及其原函数的近似曲线

The Approximate Calculation Method and Curve of Some “Beyond Element” Definite Integrals

摘要: 通常所说的“求不定积分”是指用初等函数的形式把这个不定积分表示出来，如果函数的原函数不是初等函数，则称此函数为“积不出”函数。“积不出”函数的定积分计算时“Newton-Leibniz”公式失效。本文用无穷级数理论和含参变量积分理论给出部分“积不出”函数的定积分近似计算方法，用Matlab编程数值计算部分“积不出”函数的定积分近似值，并与讨论的其广义积分值加以比较，又利用变上限函数绘制了部分“积不出”函数的原函数近似曲线。

Abstract: In general, “Calculating definite integral” is that we show the definite integral using elementary function, whereas, if the primitive function is not elementary function, then definite integral is “Beyond Element”. At this point, the “Newton-Leibniz” formula can not apply to calculate “Beyond Element” definite integral. In this paper, we apply theory of infinite series and integral depending on a parameter to calculate some “Beyond Element” definite integral. We obtain approximate value of definite integral by applying Matlab of mathematical software, and compare with analytical result of generalized integral. Subsequently, we apply variable upper limit function to plot the ap-proximate curve of primitive function.

1. 引言

在高等数学教材中，定积分的计算一般要用“Newton-Leibniz”公式，即求出被积函数的原函数，再把上下限的值代入原函数并做减法。同时，大多高等数学教材也指出，有些初等函数的原函数是非初等

函数，即我们无法用初等函数把这些函数的原函数表示出来，比如函数 ${\text{e}}^{-x^2}$ 、 $\frac{sinx}{x}$ 、 $\frac{1}{lnx}$ 、 $\frac{1}{\sqrt{1+x^4}}$ 等 [1]。

通常所说的“求不定积分”是指用初等函数的形式把这个不定积分表示出来，在这个意义下，以上函数的不定积分是求不出来的，这种函数也称为“积不出”函数。这是否意味着这些函数的定积分及广义积分我们完全计算不出来呢？否则，这些函数的定积分及广义积分该如何得到其值呢？不少同学有此疑问。本文利用无穷级数和含参变量积分的理论逐一给出以上函数的定积分的近似计算方法，并用Matlab软件计算出部分定积分的近似值，便于学生从数值上把握这些积分，也可以把该方法和程序应用到其他类似

定积分的计算中。同时，把函数 $\frac{sinx}{x}$， ${\text{e}}^{-x^2}$ 等广义积分的精确值与定积分的值放在一起，加以比较。

2. 正文

2.1. 基本引理 [2]

引理2.1：幂级数 ${\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{a}_n{x}^n$ 的和函数 $s\left(x\right)$ 在其收敛域上可积，并且逐项可积。

引理2.2：如果交错级数 ${\displaystyle \underset{n\mathrm{<mo>\; =\; </mo>1}}{\overset{\infty }{\sum }}}{\left(-1\right)}^{n-1}{u}_n$ 满足条件：

$u_n\ge u_{n+1}$ ；

$\underset{n\to \infty }{\lim }{u}_n=0$，

则级数收敛，且其和 $s\le u_1$，其余项 $r_n$ 的绝对值 $\left|r_n\right|\le u_{n+1}$。

引理2.3：若函数 $f\left(x\mathrm{,}\mu \right)$ 与 ${f^{\prime }}_{\mu }\left(x\mathrm{,}\mu \right)$ 在区域D： $a\le x<+\infty ,\alpha \le \mu \le \beta$ 上连续且无穷积分 $\phi \left(\mu \right)={\displaystyle {\int }_a^{+\infty }}f\left(x,\mu \right)\text{d}x$ 在区间 $\left[\alpha \mathrm{,}\beta \right]$ 上收敛，且无穷积分 ${\displaystyle {\int }_a^{+\infty }}{f^{\prime }}_{\mu }\left(x\mathrm{,}\mu \right)\text{d}x$ 在区间 $\left[\alpha \mathrm{,}\beta \right]$ 上一致收敛，则函数 $\phi \left(\mu \right)$ 在区间 $\left[\alpha \mathrm{,}\beta \right]$ 上可导，且 ${\phi }^{\prime }\left(\mu \right)={\displaystyle {\int }_a^{+\infty }}{f^{\prime }}_{\mu }\left(x\mathrm{,}\mu \right)\text{d}x$。

引理2.4：设函数 $f\left(x\right)$ 在区间 $\left(a\mathrm{,}b\right]$ 上连续，且 $f\left(x\right)\ge 0,x=a$ 为 $f\left(x\right)$ 的瑕点，如果存在常数 $0<q<1$ 使得

$\underset{x\to a^{+}}{\lim }{\left(x-a\right)}^{q}f(\; x\; )$

存在，则反常积分 ${\displaystyle {\int }_a^b}f\left(x\right)\text{d}x$ 收敛；

如果 $\underset{x\to a^{+}}{\lim }\left(x-a\right)f\left(x\right)=d>0$，（或 $\underset{x\to a^{+}}{\lim }\left(x-a\right)f\left(x\right)=+\infty$ )，则反常积分 ${\displaystyle {\int }_a^b}f\left(x\right)\text{d}x$ 发散。

引理2.5：设函数 $f\left(x\right)$ 在区间 $\left[a,+\infty \right)\left(a>0\right)$ 上连续，且 $f\left(x\right)\ge x$，如果存在常数 $M>0$ 且 $p>0$，使得 $f\left(x\right)\le \frac{M}{x^p}\left(a\le x<+\infty \right)$，则反常积分 ${\displaystyle {\int }_a^{+\infty }}f\left(x\right)\text{d}x$ 收敛；如果存在常数 $N>0$，使得 $f\left(x\right)\ge \frac{N}{x}$ $\left(a\le x<+\infty \right)$，则反常积分 ${\displaystyle {\int }_a^{+\infty }}f\left(x\right)\text{d}x$ 发散。

2.2. “积不出”函数的定积分的近似值与广义积分的值

例2.1：计算定积分 $I\left(y\right)={\displaystyle {\int }_0^y}{\text{e}}^{-x^2}\text{d}x$ $\left(y>0\right)$ 的近似值。

解：函数 ${\text{e}}^{-x^2}$ 的幂级数展开式为：

${\text{e}}^{-x^2}=1-x^2+\frac{x^2}{2!}-\frac{x^3}{3!}+\cdots +{\left(-1\right)}^n\frac{x^n}{n!}+\cdots \left(-\infty <x<+\infty \right)$

由引理(2.1)

$\begin{array}{c}I\left(y\right)=y-\frac{y^3}{3\cdot 1!}+\frac{y^5}{5\cdot 2!}-\frac{y^7}{7\cdot 3!}+\cdots +\frac{{\left(-1\right)}^n{y}^{2n+1}}{\left(2n+1\right)\cdot n!}+\cdots \\ ={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}}{\left(-1\right)}^n\frac{y^{2n+1}}{\left(2n+1\right)\cdot n!}\left(0<y<+\infty \right)\end{array}$

由引理(2.2)， $I\left(y\right)$ 的近似值 $I^{*}\left(y\right)={\displaystyle \underset{n=0}{\overset{k}{\sum }}}{\left(-1\right)}^n\frac{y^{2n+1}}{\left(2n+1\right)\cdot n!}$，误差 $\left|r_{2k+1}\right|<\frac{y^{2k+3}}{\left(2k+3\right)\left(k+1\right)!}$。

用Matlab计算得 $I^{*}\left(\frac{\sqrt{2}}{2}\right)=0.60501$， $I^{*}\left(\sqrt{2}\right)=0.84590$， $I^{*}\left(\frac{3\sqrt{2}}{2}\right)=0.88622$，其中 $\left|r\right|<{10}^{-5}$。且有函数图像如图1所示：

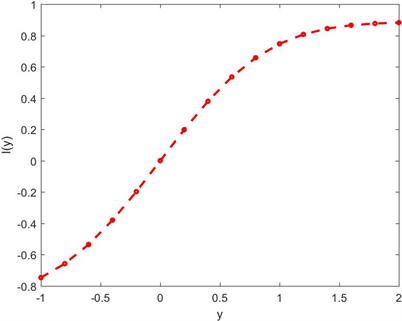
Figure 1. The graph of $I^{\mathrm{<mo>\; *\; </mo>}}(\; y\; )$

图1. $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像

因为广义积分 $I={\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-x^2}\text{d}x=\frac{\sqrt{\pi }}{2}$，注意到$ $\left|I\left(\frac{3\sqrt{2}}{2}\right)-I\right|<{10}^{-5}$，我们从数值上验证了正态分布的“ $3\sigma$ 定律” [3]。

例2.2：计算定积分 $I\left(y\right)={\displaystyle {\int }_0^y}\frac{\sin x}{x}\text{d}x$ 的近似值，讨论广义积分 $I={\displaystyle {\int }_0^{+\infty }}\frac{\sin x}{x}\text{d}x$ 的敛散性并求其值。

解：1^° $\because$ $\underset{x\to 0}{\lim }\frac{\sin x}{x}=1$ $\therefore$ $I\left(y\right)$ 不是瑕积。

$\because$ $\frac{sinx}{x}$ 是偶函数，不妨设 $y>0$，函数 $\frac{sinx}{x}$ 的幂级数展开式为：

$\frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots +{\left(-1\right)}^n\frac{x^{2n}}{\left(2n+1\right)}+\cdots \left(-\infty <x<+\infty \right)$

由引理(2.1)

$I\left(y\right)=y-\frac{y^3}{3\cdot 3!}+\frac{y^5}{5\cdot 5!}-\frac{y^7}{7\cdot 7!}+\cdots +{\left(-1\right)}^n\frac{y^{2n+1}}{\left(2n+1\right)\cdot \left(2n+1\right)!}+\cdots \left(-\infty <y<+\infty \right)$

由引理(2.2)， $I\left(y\right)$ 的近似值 $I^{*}\left(y\right)={\displaystyle \underset{n=0}{\overset{k}{\sum }}}{\left(-1\right)}^n\frac{y^{2n+1}}{\left(2n+1\right)\left(2n+1\right)!}$，误差 $\left|r_{2k+1}\right|<\frac{y^{2k+3}}{\left(2k+3\right)\left(2k+3\right)!}$。

2^°判定广义积分 $I={\displaystyle {\int }_0^{+\infty }}\frac{\sin x}{x}\text{d}x$ 的敛散性，并求其值。

$\because$ $\left|{\displaystyle {\int }_0^a}\sin x\text{d}x\right|\le 2$， $\frac{1}{x}\to 0\left(x\to +\infty \right)$ 且 $\frac{1}{x}$ 递减，由Dirichlet判别法 [4] 知I是收敛的，

由Abel判别法 [4] 知含参量积分 $I\left(t\right)={\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-tx}\frac{\sin x}{x}\text{d}x$ 在 $t\in \left[\mathrm{0,}+\infty \right)$ 上一致收敛。

$I=I\left(0\right)=\underset{t\to 0^{+}}{\lim }I\left(t\right)$，由Weierstrass判别法 [4] 知 ${\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-tx}\frac{sinx}{x}\text{d}x$ 在 $\left[t_0\mathrm{,}+\infty \right)$ 上一致收敛 $\left(t_0>0\right)$。

根据引理(2.3)利用Dirichlet判别法 [4]，考虑 $I\left(u\right)={\displaystyle {\int }_a^u}f\left(x\right)\text{d}x$ 在 $\left(a\mathrm{,}+\infty \right)$ 上有界， $g\left(x\right)$ 在 $\left[a\mathrm{,}+\infty \right)$ 上

当 $x\to +\infty$ 时单调趋于0，则 ${\displaystyle {\int }_a^{+\infty }}f\left(x\right)g\left(x\right)\text{d}x$ 收敛。

$I^{\prime }\left(t\right)=-{\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-tx}\sin x\text{d}x={\frac{{\text{e}}^{-tx}\left(t\sin x+\cos x\right)}{1+t^2}|}_0^{+\infty }=-\frac{1}{1+t^2}$，则 $I\left(t\right)=-\arctan t+C$。

又 $\left|I\left(t\right)\right|=\left|{\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-tx}\frac{\sin x}{x}\text{d}x\right|\le {\displaystyle {\int }_0^{+\infty }}{\text{e}}^{-tx}\text{d}x=\frac{1}{t}\to 0\left(t\to +\infty \right)$，即 $\underset{t\to +\infty }{\lim }I\left(t\right)=0$， $C=\frac{\pi }{2}$，

故 $I\left(t\right)=-\arctan t+\frac{\pi }{2}$， $I=I\left(0\right)=\frac{\pi }{2}$。

用Matlab计算得 $I^{\mathrm{<mo>\; *\; </mo>}}\left(\pi \right)=1.85193$， $I^{\mathrm{<mo>\; *\; </mo>}}\left(2\pi \right)=1.41815$， $I^{\mathrm{<mo>\; *\; </mo>}}\left(3\pi \right)=1.67476$， $I^{\mathrm{<mo>\; *\; </mo>}}\left(4\pi \right)=1.49216$，这里 $\left|r\right|<{10}^{-5}$，并给出了 $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像，如图2所示。

例2.3：计算定积分 $I\left(y\right)={\displaystyle {\int }_{\text{e}}^y}\frac{1}{\ln x}\text{d}x$ 的近似值 $\left(y>\text{e}\right)$，讨论广义积分 $I_1={\displaystyle {\int }_{\text{e}}^{+\infty }}\frac{1}{\ln x}\text{d}x$， $I_2={\displaystyle {\int }_0^1}\frac{1}{\ln x}\text{d}x$， $I_3={\displaystyle {\int }_1^2}\frac{1}{\ln x}\text{d}x$ 的敛散性。

解：1^° $I\left(y\right)={\displaystyle {\int }_{\text{e}}^y}\frac{1}{\ln x}\text{d}x\stackrel{t=\ln x}{{\displaystyle =}}{\displaystyle {\int }_1^{\ln y}}\frac{1}{t}\cdot {\text{e}}^t\text{d}t$，

$\frac{{\text{e}}^t}{t}$ 的幂级数展开式为：

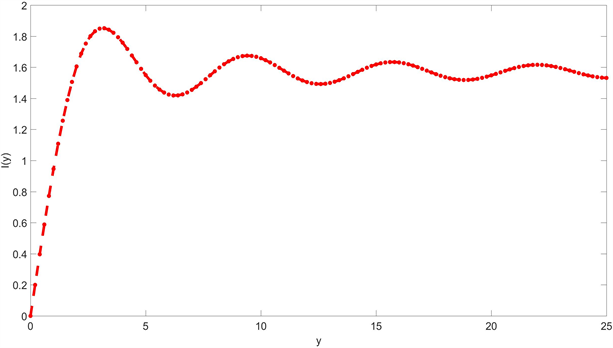
Figure 2. The Graph of $I^{\mathrm{<mo>\; *\; </mo>}}(\; y\; )$

图2. $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像

$\frac{{\text{e}}^t}{t}=\frac{1}{t}+1+\frac{t}{2}+\frac{t^2}{3!}+\cdots +\frac{t^{n-1}}{n!}+\cdots$ ( $-\infty <t<0$ 或 $0<t<+\infty$ )。

由(2.1)

$\begin{array}{c}I\left(y\right)={\displaystyle {\int }_1^{\ln y}}\left(\frac{1}{t}+1+\frac{t}{2!}+\frac{t^2}{3!}+\cdots +\frac{t^{n-1}}{n!}+\cdots \right)\text{d}t\\ =\ln \ln y+\left(\ln y-1\right)+{\displaystyle \underset{n=2}{\overset{\infty }{\sum }}}\frac{{\left(\ln y\right)}^n-1}{n\cdot n!}\left(\text{e}<y\right)\end{array}$

$I^{*}\left(y\right)=\ln \ln y+\left(\ln y-1\right)+{\displaystyle \underset{n=2}{\overset{k}{\sum }}}\frac{{\left(\ln y\right)}^n-1}{n\cdot n!}$ 不能估算误差。

用Matlab计算得到 $I^{\mathrm{<mo>\; *\; </mo>}}\left(\text{e}\right)=0$， $I^{\mathrm{<mo>\; *\; </mo>}}\left({\text{e}}^2\right)=3.059116$， $I^{*}\left({\text{e}}^3\right)=8.038714$， $I^{\mathrm{<mo>\; *\; </mo>}}\left({\text{e}}^4\right)=17.735756$，从计算结果可以看出 $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的值增大速度较快，导致 ${\displaystyle {\int }_{\text{e}}^{+\infty }}\frac{1}{lnx}\text{d}x$ 发散。以下为 $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像，如图3所示。

2^° 讨论 $\begin{array}{l}{I}_1\mathrm{,}{I}_2\mathrm{,}{I}_3\hfill \end{array}$ 的敛散性， $\frac{1}{\ln x}>\frac{1}{x}$ $\left(\text{e}\le x<+\infty \right)$，由引理(2.5)知， $I_1$ 发散。

$\because$ $\underset{x\to 0}{\lim }\frac{1}{lnx}=0$， $\underset{x\to 1}{\lim }\frac{1}{\ln x}=\infty$， $\therefore$ $I_2$ 中仅 $x=1$ 为瑕点。而 $\underset{x\to 1^{-}}{\lim }\left(1-x\right)\frac{1}{\ln x}=1>0$，由引理(2.4)知 $I_2$ 发散。类似地，由引理(2.4)知 $I_3$ 发散。

例2.4：计算定积分 $I\left(y\right)={\displaystyle {\int }_0^y}\frac{1}{\sqrt{1+x^4}}\text{d}x$ 的近似值，并讨论广义积分 $I={\displaystyle {\int }_0^{+\infty }}\frac{1}{\sqrt{1+x^4}}\text{d}x$ 的敛散性。

解：1^° 函数 $\frac{1}{\sqrt{1+x^4}}$ 的幂级数展开式为：

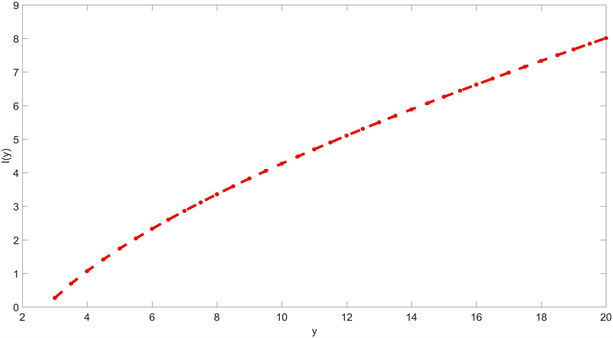
Figure 3. The Graph of $I^{\mathrm{<mo>\; *\; </mo>}}(\; y\; )$

图3. $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像

$\frac{1}{\sqrt{1+x^4}}=1-\frac{1}{2}{x}^4+\frac{1\cdot 3}{2\cdot 4}{x}^8-\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}{x}^{12}+\frac{1\cdot 3\cdot 5\cdot 7}{2\cdot 4\cdot 6\cdot 8}{x}^{16}+\cdots +{\left(-1\right)}^n\frac{\left(2n-1\right)!!}{\left(2n\right)!!}{x}^{4n}+\cdots \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\left(x\in \left[0,1\right]\right)$

由引理(2.1) $I\left(y\right)=y+{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}\frac{{\left(-1\right)}^n\left(2n-1\right)!!}{\left(4n+1\right)\left(2n\right)!1}{y}^{4n+1}$ $\left(0\le y\le 1\right)$，由引理(2.2) $I\left(y\right)$ 的近似值 $I^{*}\left(y\right)=y+{\displaystyle \underset{n=1}{\overset{k}{\sum }}}\frac{{\left(-1\right)}^n\left(2n-1\right)!!}{\left(4n+1\right)\left(2n\right)!1}{y}^{4n+1}$，误差 $\left|r_{4k+1}\right|\le \frac{\left(2k+1\right)!!}{\left(4k+5\right)\cdot \left(2k+2\right)!!}{y}^{4k+5}$。用Matlab计算得 $I^{*}\left(\frac{1}{2}\right)=0.49695$， $I^{*}\left(1\right)=0.92778$，这里 $\left|r\right|<{10}^{-5}$，且有 $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的图像，如图4所示。

Figure 4. The Graph of $I^{\mathrm{<mo>\; *\; </mo>}}(\; y\; )$

图4. $I^{\mathrm{<mo>\; *\; </mo>}}\left(y\right)$ 的函数图像

2^° $\because$ $\frac{1}{\sqrt{1+x^4}}<\frac{1}{x^2}$ $x\in \left(\mathrm{0,}+\infty \right)$

由引理(2.4)广义积分 ${\displaystyle {\int }_0^{+\infty }}\frac{1}{\sqrt{1+x^4}}\text{d}x$ 收敛。令 $I_1={\displaystyle {\int }_0^1}\frac{1}{\sqrt{1+x^4}}\text{d}x$， $I_2={\displaystyle {\int }_1^{+\infty }}\frac{1}{\sqrt{1+x^4}}\text{d}x$，由定积分估值定理知 $\frac{\sqrt{2}}{2}<I_1<1$，由不等式性质得 ${\displaystyle {\int }_1^{+\infty }}\frac{\sqrt{2}}{2}\cdot \frac{1}{x^2}\text{d}x<I_2<{\displaystyle {\int }_1^{+\infty }}\frac{1}{x^2}\text{d}x$，即 $\frac{\sqrt{2}}{2}<I_2<1$。

故 $\sqrt{2}<I=I_1+I_2<2$。

3. 总结

对于“积不出”函数的定积分和广义积分，可以借助无穷级数和含参量积分以及估值等方法得到其近似值，甚至精确值。利用变上限函数的性质借助MATLAB画出原函数的大致图像，综合数学分析的知识，可用此方法研究这类“积不出”函数的定积分近似值及原函数图像。

基金项目

中国石油大学(北京)克拉玛依校区科研启动基金资助(No.XQZX20160024)“Supported by Research Foundation of China University of Petroleum-Beijing at Karamay (No.XQZX20160024)”。

参考文献