一种基于ALD和AEP分布的贝叶斯分位数回归

A Bayesian Quantile Regression Based on ALD and AEP Distribution

摘要: 本文采用非对称指数幂分布(AEP)与非对称拉普拉斯分布(ALD)对分位数回归模型的误差项进行假定，对此进行贝叶斯分位数回归的参数估计。针对参数后验密度的复杂性，采用吉布斯抽样算法，对ALD分布和AEP分布进行后验参数抽样。通过数值模拟结果可知，服从AEP分布的误差假定对数据的适应性比ALD分布的要强。

Abstract: In this paper, the asymmetric exponential power distribution (AEP) and asymmetric Laplace distribution (ALD) are used to make assumptions about the error terms of the quantile regression model, and the parameters of Bayesian quantile regression are estimated for this. Aiming at the complexity of the posterior density of parameters, the Gibbs sampling algorithm is used to sample the posterior parameters of the ALD distribution and AEP distribution. According to the numerical simulation results, the error following the AEP distribution is assumed to be more adaptable to the data than the ALD distribution.

1. 引言

分位数回归模型传承于经典最小二乘回归模型，相比于经典最小二乘回归模型，分位数回归模型提供了更多的信息，有利于解释因变量与自变量之间的关系。近年来，分位数回归在各个领域得到广泛的应用，很多学者越来越关注因变量在任意分位数水平下与自变量的关系。

1978年Koenker首次提出“分位数回归”概念 [1]，用于解释因变量与自变量之间的关系。1999年Koenker和Machado研究了非对称拉普拉斯分布和分位数回归之间的关系 [2]。2001年Keming Yu [3] 介绍了一种贝叶斯分位数回归思想，采用基于非对称拉普拉斯分布对参数进行估计，并证实无论数据的原始分布如何，使用非对称拉普拉斯分布对贝叶斯分位数回归建模是一种非常自然且有效的方法。自此，贝叶斯估计方法在分位数回归中有越来越多的应用。

目前，对于分位数回归模型的研究，基本集中在贝叶斯分位数估计、离散选择分位数回归估计、分位数处理效应模型以及无条件分位数回归方法的研究。针对贝叶斯分位数回归估计，它的关键在于将误差项设定为服从某种分布，由于非对称指数幂分布的优良性质比非对称拉普拉斯分布较好，而且非对称拉普拉斯分布还是非对称指数幂分布的一个特例，本文利用这一思想，使用非对称指数幂分布的似然函数来进行贝叶斯分位数回归参数估计。

2. 非对称拉普拉斯分布与非对称指数幂分布

对贝叶斯分位数回归模型进行参数估计，需要假定分位数回归中的误差项服从非对称拉普拉斯分布或者非对称指数幂分布。根据概率密度函数构建极大似然函数，依据贝叶斯定理，从参数先验分布中求解后验分布。两种分布的概率密度函数如下：

非对称拉普拉斯分布(Asymmetric Laplace Distribution, ALD)的概率密度函数为：

$f\left(y;\mu ,\sigma ,p\right)=\frac{p\left(1-p\right)}{\sigma }\exp \left\{-\frac{y-\mu }{\sigma }\left[p-I\left(y\le \mu \right)\right]\right\},y\in \left(-\infty ,+\infty \right)$ (1)

其中， $0<p<1$ 为偏度参数， $\sigma >0$ 为尺度参数， $-\infty <\mu <+\infty$ 为位置参数。

非对称指数幂分布(Asymmetric Exponential Power Distribution, AEPD)是由Zhu Dongming [4] 等提出的，其概率密度函数为：

$f_{\text{AEP}}\left(y|\mu ,\sigma ,\alpha ,p_1{p}_2\right)=\{\begin{array}{l}\frac{1}{\sigma }\exp \left(-{\left|\frac{y-\mu }{\alpha \sigma /\Gamma \left(1+p_1\right)}\right|}^{p_1}\right),y\le \mu \\ \frac{1}{\sigma }\exp \left(-{\left|\frac{y-\mu }{\left(1-\alpha \right)\sigma /\Gamma \left(1+p_2\right)}\right|}^{p_2}\right),y>\mu \end{array}$ (2)

其中， $\text{Γ}\left(x\right)$ 为gamma函数， $0<\alpha <1$ 为偏度参数， $\sigma >0$ 为尺度参数， $p_1>0$ 和 $p_2>0$ 分别控制左尾和右尾参数， $-\infty <\mu <+\infty$ 为位置参数。当 $\alpha =\frac{1}{2}$ 和 $p_1=p_2$ 时，AEPD分布为对称的指数幂分布；当 $\alpha =\frac{1}{2}$ 和 $p_1=p_2=2$ 时，AEPD分布为标准的正态分布；当 $p_1=p_2=1$ 时便是ALD分布； $p_1\left(p_2\right)$ 值越小，则左尾(右尾)越厚， $\alpha$ 值越大，则分布呈现为左偏。

3. 贝叶斯分位数回归

在进行贝叶斯分位数回归模型的参数估计时，需要构建一般线性回归模型，假定回归模型中的误差项服从ALD分布与AEP分布，对此构建相应的似然函数。通过贝叶斯定理、参数先验分布求解该分布的后验分布。由于似然函数的复杂性，为了更快的求解后验分布，采用吉布斯抽样算法的思想。

3.1. 设线性回归模型

$y_i={\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_k{x}_{ik}+{\epsilon }_i,i=1,\cdots ,n;k=1,\cdots ,n$ (3)

其中， $x_i$ 为自变量， $y_i$ 为因变量， ${\beta }_k$ 为未知参数向量，误差项 ${\epsilon }_i~\text{ALD}\left(0,1,\tau \right)$ 和 ${\epsilon }_i~\text{AEP}\left(0,\sigma ,\alpha ,p_1,p_2\right)$。

3.2. 非对称拉普拉斯分布似然函数(ALD)

根据假设分位数回归模型的误差项服从ALD分布，其似然函数为：

$L\left(y_i|x_i^{\text{T}}\beta ,\sigma ,p\right)=\frac{p^n{\left(1-p\right)}^n}{{\sigma }^n}\exp \left\{-\frac{1}{\sigma }{\displaystyle \underset{i}{\sum }{\rho }_p\left(y_i-x_i^{\text{T}}\beta \right)}\right\}$ (4)

其中， ${\rho }_{\tau }\left(u\right)=u\left(p-I\left(u<0\right)\right)$。

为了在分位数回归中采用吉布斯算法，因此参考2011年Kozumi和Kobayashi [5] 在文章中给出的吉布斯抽样方法，对此进行贝叶斯分位数回归参数估计。

3.3. 非对称指数幂分布似然函数(AEPD)

Naranjo在2012 [6] 和2015 [7] 年对SEP分布和AEP分布进行相关的研究，提出了关于非对称指数幂相关的理论和方法。

设 $Y|\left[U_1=u_1\right]~U\left(\mu -\frac{\alpha \sigma }{\Gamma \left(1+\frac{1}{p_1}\right)}{u}_1^{\frac{1}{p_1}},\mu \right)$， $U_1~Ga\left(1+\frac{1}{p_1},1\right)$，且概率为 $\alpha$，和 $Y|[U_2=u_2]~U\left(\mu ,\mu +\frac{\left(1-\alpha \right)\sigma }{\Gamma \left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}\right)$， $U_2~Ga\left(1+\frac{1}{p_2},1\right)$，且概率为 $\left(1-\alpha \right)$，则 $Y~\text{AEP}\left(\mu ,\sigma ,\alpha ,p_1,p_2\right)$。

根据假设分位数回归模型的误差项服从AEPD分布，其似然函数为：

$\begin{array}{l}L\left(y,x,u_1,u_2|\beta ,\sigma ,\alpha ,p_1,p_2\right)\\ =\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\frac{1}{\sigma }\{\exp \left(-u_1\right)I\left[x_i^{\text{T}}\beta -\frac{\alpha \sigma }{\Gamma \left(1+\frac{1}{p_1}\right)}{u}_1^{\frac{1}{p_1}}<y_i<x_i^{\text{T}}\beta \right]\\ +\exp \left(-u_2\right)I\left[x_i^{\text{T}}\beta <y_i<x_i^{\text{T}}\beta +\frac{\left(1-\alpha \right)\sigma }{\Gamma \left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}\right]\}\end{array}$ (5)

其中， $y={\left(y_1,\cdots ,y_n\right)}^{\text{T}}$， $u_1={\left(u_{11},\cdots ,u_{1n}\right)}^{\text{T}}$， $u_2={\left(u_{21},\cdots ,u_{2n}\right)}^{\text{T}}$， $x={\left(x_1,\cdots ,x_n\right)}^{\text{T}}$， $\beta ={\left({\beta }_1,\cdots ,{\beta }_n\right)}^{\text{T}}$。

根据贝叶斯定理，参数的联合后验密度为：

$\begin{array}{l}P\left(u_1,u_2,\beta ,\sigma ,\alpha ,p_1,p_2|y,x\right)\\ \propto f\left(\beta \right)f\left(\sigma \right)f\left(\alpha \right)f\left(p_1\right)f\left(p_2\right){\sigma }^{-n}\\ \times \underset{i=1}{\overset{n}{{\displaystyle \sum }}}(\exp \left(-u_1\right)\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\frac{1}{\sigma }\{\exp \left(-u_1\right)I\left[x_i^{\text{T}}\beta -\frac{\alpha \sigma }{\Gamma \left(1+\frac{1}{p_1}\right)}{u}_1^{\frac{1}{p_1}}<y_i<x_i^{\text{T}}\beta \right]\\ +\exp \left(-u_2\right)I\left[x_i^{\text{T}}\beta <y_i<x_i^{\text{T}}\beta +\frac{\left(1-\alpha \right)\sigma }{\Gamma \left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}\right]\})\end{array}$ (6)

其中， $f\left(\beta \right),f\left(\sigma \right),f\left(\alpha \right),f\left(p_1\right),f\left(p_2\right)$ 均为待估参数的先验密度函数。

设定参数的先验分布为：

$\{\begin{array}{l}{u}_1,u_2~Exp\left(1\right)\\ \sigma ~IG\left(a_{\sigma },b_{\sigma }\right)\\ \alpha ~Beta\left(a_{\alpha },b_{\alpha }\right)\\ p_1,p_2~N\left(a_{p_i},b_{p_i}\right)\\ \beta ~N_k\left(b,B\right)\end{array}$ (7)

其中， $Exp\left(1\right)$ 为参数为1的指数分布，IG为逆伽玛分布，Beta为贝塔分布，N为正态分布， $N_k$ 为多元正态分布。

根据贝叶斯定理可得参数的待估后验密度为：

1) $u_1,u_2$

$\begin{array}{l}P\left(u_{1i}|y,x,\beta ,\sigma ,\alpha ,p_1,p_2\right)\\ \propto f\left(u_{1i}\right)I\left[u_{1i}>{\left(\frac{\left(x_i^{\text{T}}\beta -y_i\right)\text{Γ}\left(1+\frac{1}{p_1}\right)}{\alpha \sigma }\right)}^{p_1}\right]\left(y_i<x_i^{\text{T}}\beta \right)\\ \propto Exp\left(1\right)I\left[u_{1i}>{\left(\frac{\left(x_i^{\text{T}}\beta -y_i\right)\text{Γ}\left(1+\frac{1}{p_1}\right)}{\alpha \sigma }\right)}^{p_1}\right]\left(y_i<x_i^{\text{T}}\beta \right)\end{array}$ (8)

$\begin{array}{l}P\left(u_{2i}|y,x,\beta ,\sigma ,\alpha ,p_1,p_2\right)\\ \propto f\left(u_{2i}\right)I\left[u_{2i}>{\left(\frac{\left(y_i-x_i^{\text{T}}\beta \right)\Gamma \left(1+\frac{1}{p_2}\right)}{\left(1-\alpha \right)\sigma }\right)}^{p_2}\right]\left(y_i>x_i^{\text{T}}\beta \right)\\ \propto Exp\left(1\right)I\left[u_{2i}>{\left(\frac{\left(y_i-x_i^{\text{T}}\beta \right)\Gamma \left(1+\frac{1}{p_2}\right)}{\left(1-\alpha \right)\sigma }\right)}^{p_2}\right]\left(y_i>x_i^{\text{T}}\beta \right)\end{array}$ (9)

其中， $I(\cdot )$ 为指示函数。

2) $\sigma$

$\begin{array}{l}P\left(\sigma |y,x,u_1,u_2,\alpha ,\beta ,p_1,p_2\right)\\ \propto f\left(\sigma \right)\frac{1}{{\sigma }^n}I\left[\sigma >\underset{\_}{\sigma }\right]\\ \propto IG\left(n-1+a_{\sigma },b_{\sigma }\right)I\left[\sigma >\underset{\_}{\sigma }\right]\end{array}$ (10)

当 $u_{1i}>0$ 时， $x_i^{\text{T}}\beta -\frac{\alpha \sigma }{\Gamma \left(1+\frac{1}{p_1}\right)}{u}_{1i}^{\frac{1}{p_1}}<y_i$，化简为：

$\sigma >\frac{\left(x_i^{\text{T}}\beta -y_i\right)\Gamma \left(1+\frac{1}{p_1}\right)}{\alpha u_{1i}^{1/p_1}}$

当 $u_{2i}>0$ 时， $y_i<x_i^{\text{T}}\beta +\frac{\left(1-\alpha \right)\sigma }{\Gamma \left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}$，化简为：

$\sigma >\frac{\left(y_i-x_i^{\text{T}}\beta \right)\Gamma \left(1+\frac{1}{p_2}\right)}{\left(1-\alpha \right)u_{2i}^{1/p_2}}$

由此可得： $\underset{\_}{\sigma }=\max \{\frac{\left(x_i^{\text{T}}\beta -y_i\right)\text{Γ}\left(1+\frac{1}{p_1}\right)}{\alpha u_{1i}^{1/p_1}},\frac{\left(y_i-x_i^{\text{T}}\beta \right)\text{Γ}\left(1+\frac{1}{p_2}\right)}{\left(1-\alpha \right)u_{2i}^{1/p_2}}\}$。

3) $\alpha$

$P\left(\alpha |y,x,u_1,u_2,\sigma ,\beta ,p_1,p_2\right)\propto f\left(\alpha \right)I\left[\underset{\_}{\alpha }<\alpha <\bar{\alpha }\right]\propto Beta\left(a_{\alpha },b_{\alpha }\right)I\left[\underset{\_}{\alpha }<\alpha <\bar{\alpha }\right]$ (11)

当 $u_{1i}>0,u_{2i}>0$ 时，有 $x_i^{\text{T}}\beta -\frac{\alpha \sigma }{\text{Γ}\left(1+\frac{1}{p_1}\right)}{u}_{1i}^{\frac{1}{p_1}}<y_i<x_i^{\text{T}}\beta +\frac{\left(1-\alpha \right)\sigma }{\text{Γ}\left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}$

化简可得： $\max \left\{0,\frac{\left(x_i^{\text{T}}\beta -y_i\right)\text{Γ}\left(1+\frac{1}{p_1}\right)}{\sigma u_{1i}^{1/p_1}}\right\}<\alpha <\min \left\{0,1-\frac{\left(y_i-x_i^{\text{T}}\beta \right)\text{Γ}\left(1+\frac{1}{p_2}\right)}{\sigma u_{2i}^{1/p_2}}\right\}$

$\underset{\_}{\alpha }=\max \left\{0,\frac{\left(x_i^{\text{T}}\beta -y_i\right)\text{Γ}\left(1+\frac{1}{p_1}\right)}{\sigma u_{1i}^{\frac{1}{p_1}}}\right\}$

$\bar{\alpha }=\min \left\{0,1-\frac{\left(y_i-x_i^{\text{T}}\beta \right)\text{Γ}\left(1+\frac{1}{p_2}\right)}{\sigma u_{2i}^{1/p_2}}\right\}$

4) $p_1,p_2$

$\begin{array}{l}P\left(p_1|y,x,u_1,u_2,\alpha ,\sigma ,\beta ,p_2\right)\\ \propto f\left(p_1\right)I\left[\frac{x_i^{\text{T}}\beta -y_i}{\alpha \sigma }<\frac{u_{1i}^{1/p_1}}{\text{Γ}\left(1+\frac{1}{p_1}\right)}\right]\left(u_{1i}>0\right)\\ \propto N\left(a_{p_1},b_{p_1}\right)I\left[\frac{x_i^{\text{T}}\beta -y_i}{\alpha \sigma }<\frac{u_{1i}^{1/p_1}}{\text{Γ}\left(1+\frac{1}{p_1}\right)}\right]\left(u_{1i}>0\right)\end{array}$ (12)

$\begin{array}{l}P\left(p_2|y,x,u_1,u_2,\alpha ,\sigma ,\beta ,p_1\right)\\ \propto f\left(p_2\right)I\left[\frac{y_i-x_i^{\text{T}}\beta }{\left(1-\alpha \right)\sigma }<\frac{u_{2i}^{1/p_2}}{\text{Γ}\left(1+\frac{1}{p_2}\right)}\right]\left(u_{2i}>0\right)\\ \propto N\left(a_{p_2},b_{p_2}\right)I\left[\frac{y_i-x_i^{\text{T}}\beta }{\left(1-\alpha \right)\sigma }<\frac{u_{2i}^{1/p_2}}{\text{Γ}\left(1+\frac{1}{p_2}\right)}\right]\left(u_{2i}>0\right)\end{array}$ (13)

5) $\beta$

设 ${\beta }_{-j}^{\text{T}}=\left({\beta }_1,\cdots ,{\beta }_{j-1},{\beta }_{j+1},\cdots ,{\beta }_k\right)$ 为不含第j个参数的向量， $\beta$ 的先验分布服从多元正态分布，根据贝叶斯定理和多元正态分布性质可得：

$\begin{array}{l}P\left({\beta }_j|y,x,u_1,u_2,{\beta }_{-j},\alpha ,\sigma ,\beta ,p_1,p_2\right)\\ \propto f\left({\beta }_j\right)I\left[{\beta }_j\in \left({\underset{\_}{\beta }}_j,{\bar{\beta }}_j\right)\right]\propto N\left(b_j^{*},B_j^{*}\right)I\left[{\beta }_j\in \left({\underset{\_}{\beta }}_j,{\bar{\beta }}_j\right)\right]\end{array}$ (14)

其中， $j=1,\cdots ,k$， $b_j^{\text{*}}=b_j-B_{j\left(-j\right)}{B}_{\left(-j\right)\left(-j\right)}^{-1}\left({\beta }_{\left(-j\right)}-b_{\left(-j\right)}\right)$， $B_j^{\text{*}}=B_{jj}-B_{j\left(-j\right)}{B}_{\left(-j\right)\left(-j\right)}^{-1}{B}_{\left(-j\right)j}$；由似然函数可知：

$x_i^{\text{T}}\beta -\frac{\alpha \sigma }{\text{Γ}\left(1+\frac{1}{p_1}\right)}{u}_1^{\frac{1}{p_1}}<y_i<x_i^{\text{T}}\beta +\frac{\left(1-\alpha \right)\sigma }{\text{Γ}\left(1+\frac{1}{p_2}\right)}{u}_2^{\frac{1}{p_2}}$

当 $x_{ij}>0$ 时，化简为：

$\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}-\frac{\left(1-\alpha \right)\sigma u_{2i}^{1/p_2}}{x_{ij}\text{Γ}\left(1+1/p_2\right)}<{\beta }_j<\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}+\frac{\alpha \sigma u_{1i}^{1/p_1}}{x_{ij}\text{Γ}\left(1+1/p_1\right)}$

当 $x_{ij}<0$ 时，化简为：

$\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}+\frac{\alpha \sigma u_{1i}^{1/p_1}}{x_{ij}\text{Γ}\left(1+1/p_1\right)}<{\beta }_j<\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}-\frac{\left(1-\alpha \right)\sigma u_{2i}^{1/p_2}}{x_{ij}\text{Γ}\left(1+1/p_2\right)}$

由此可得：

${\underset{\_}{\beta }}_j=\left\{\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}-\frac{\left(1-\alpha \right)\sigma u_{2i}^{\frac{1}{p_2}}}{x_{ij}\text{Γ}\left(1+\frac{1}{p_2}\right)},\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}+\frac{\alpha \sigma u_{1i}^{1/p_1}}{x_{ij}\text{Γ}\left(1+1/p_1\right)}\right\}$

${\bar{\beta }}_j=\left\{\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}+\frac{\alpha \sigma u_{1i}^{\frac{1}{p_1}}}{x_{ij}\text{Γ}\left(1+\frac{1}{p_1}\right)},\frac{y_i-x_{i\left(-j\right)}^{\text{T}}{\beta }_{\left(-j\right)}}{x_{ij}}-\frac{\left(1-\alpha \right)\sigma u_{2i}^{1/p_2}}{x_{ij}\text{Γ}\left(1+1/p_2\right)}\right\}$

4. 数据模拟分析

针对一般化的形式，数据由以下设定生成：

$\{\begin{array}{l}{y}_i={\beta }_1{x}_1+{\beta }_2{x}_2+{\epsilon }_i,i=1,2,\cdots ,n\\ x_i~unif\left(0,100\right)\\ {\beta }_1=3,{\beta }_2=2,\end{array}$ (15)

由于不同的误差项分布会影响分位数回归系数的变化，本文将讨论误差项 ${\epsilon }_i~\text{ALD}\left(0,1,p\right)$ 和 ${\epsilon }_i~\text{AEP}\left(0,\sigma ,\alpha ,p_1,p_2\right)$，生成两种不同的模拟数据。

图1给出了标准化非对称拉普拉斯分布的密度图。从中可以看到，随着偏度参数(p)不断的变化，该分布也呈现出不同的变化：当 $p=0.1$ 时，ALD密度图的取值集中在中右尾，当 $p=0.3$ 时，ALD密度图呈现左偏现象，取值偏在右尾，当 $p=0.5$ 时，两侧分布是对称的。

Figure 1. Normalized asymmetric Laplace distribution (ALD) density map

图1. 标准化非对称拉普拉斯分布(ALD)密度图

图2给出了非对称指数幂分布(AEPD)随偏度参数( $\alpha$ )变化密度图。从图中可以看到，随着偏度参数 $\alpha$ 不断的增大，该图呈现左偏现象。

Figure 2. Density diagram of asymmetric exponential power distribution (AEPD) with skewness parameter (α)

图2. 非对称指数幂分布(AEPD)随偏度参数(α)变化密度图

图3给出了非对称指数幂分布(AEPD)随着左尾参数( $p_1$ )变化密度图。从图中可以看出，随着左尾参数 $p_1$ 不断的减小，该分布呈现左尾厚重的现象。

Figure 3. Density diagram of asymmetric exponential power distribution (AEPD) as a function of the left tail parameter ( p 1 )

图3. 非对称指数幂分布(AEPD)随着左尾参数( $p_1$ )变化密度图

图4给出了非对称指数幂分布(AEPD)随着左尾参数( $p_2$ )变化密度图。从图中可以看出，随着左尾参数 $p_2$ 不断的减小，该分布呈现右尾厚重的现象。

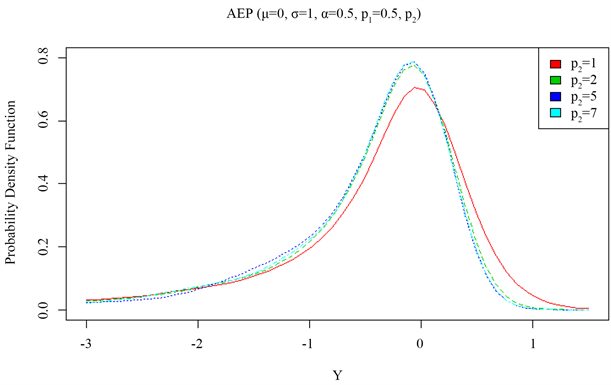
Figure 4. Density diagram of asymmetric exponential power distribution (AEPD) with the right tail parameter ( p 2 )

图4. 非对称指数幂分布(AEPD)随右尾参数( $p_2$ )变化密度图

针对模型(15)产生相应的分布数据，ALD分布随机数可由R语言中ald包中的rALD函数生成；对于AEPD分布随机数可由3.3节中生成。采用Gibbs抽样算法对两种分布进行参数抽样，在对非对称指数幂分布进行参数抽样时，可依据(8)、(9)、(10)、(11)、(12)、(13)和(14)进行贝叶斯条件后验密度参数抽取。从条件后验密度中可以看出，对每种共轭分布进行参数抽样时，都必须进行截断处理，可使用R语言中的LaplacesDemon包，对常见的截断分布进行随机数抽样。

Table 1. Comparison table of estimated simulated values and true values following ALD distribution and AEP distribution

表1. 服从ALD分布和AEP分布的估计模拟值与真值对照表

从上表1中可以看出，非对称指数幂分布对于贝叶斯分位数回归来说是非常适应的，由于非对称指数幂的优势，在处理数据的偏度和重尾时，非对称拉普拉斯分布就稍逊一些，ALD分布只能处理偏度问题，对于拖尾的数据，ALD分布并没有参数对其进行控制，所以AEP分布相对处理起来就比ALD分布灵活一些，也更适合现在的数据。在低分位点和高分位点可以看出，对于未知参数的估计有所变化，ALD分布的参数估计使得参数值在变小，而AEP分布的参数估计却在变大。也可以看到，AEP分布在其他未知参数的估计也比较接近真实值；在样本量为25时，AEP分布的模拟结果更加接近真实真；在样本量为100时，各分位点下，AEP分布的模拟结果都稍接近真实值。

图5中给出了样本量为100时，迭代5000次，去掉前500次，服从ALD分布的 ${\beta }_1$， ${\beta }_2$ 在0.25分位点的MCMC抽样轨迹图，可以看出，均在设定值上下波动，因此抽样构成的马尔科夫链收敛。

Figure 5. Traces of MCMC sampling values of ${\beta }_1$ and ${\beta }_2$ following ALD distribution

图5. 服从ALD分布的 ${\beta }_1$， ${\beta }_2$ 的MCMC抽样值轨迹图

图6中给出了样本量为100时，迭代5000次，去掉前300次，服从AEP分布的 ${\beta }_1$， ${\beta }_2$ 在0.25分位点的MCMC抽样轨迹图，可以看出，均在设定值上下波动，因此抽样构成的马尔科夫链收敛。

Figure 6. Traces of MCMC sampled values of ${\beta }_1$ and ${\beta }_2$ following AEP distribution

图6. 服从AEP分布的 ${\beta }_1$， ${\beta }_2$ 的MCMC抽样值轨迹图

5. 结束语

本文对贝叶斯分位数回归的参数估计，从以往的ALD分布扩展到AEP分布，并对ALD分布和AEP分布进行Gibbs算法抽样。从ALD分布和AEP分布的密度图可以看出，AEP分布相对于ALD分布来说对于数据的适应性更强。从模拟的情况来看，AEP分布针对数据在低分位和高分位时，参数的估计值会比较接近真值，这也体现了它的优势。由于AEP分布的特点，AEP分布在金融数据中会得到更好的运用，由于金融数据的复杂性，ALD分布在厚尾状况下，无法对数据进行处理，而AEP分布刚好能处理这方面的问题。