1. 引言
本科教育承担着教导学生如何做人以及培养学生专业技能的重任,其对学生的品性修养、政治态度以及专业技能的培养与训练对学生将来能否适应社会以及实现个人价值产生着深远的影响。因此,国家对于本科教育的重视程度非常之大。而随着中国的改革开放,国家的综合实力不断增强,中国高等教育发展整体也已经进入了世界中上水平。
众所周知,江苏省的教育一直是全国的典范,其本科教育的发展在全国名列前茅。然而,由于地域和历史的影响,江苏省13个地级市的本科教育发展并不平衡,这种不平衡具体体现在本科院校数量、招生人数、师资队伍与结构、生师比、教学条件与利用、专业建设与教学改革、学生就业、科技投入与产出以及双一流学科建设等9个指标上。
2. 基于改进的主成分分析方法的综合评价模型
本文主要围绕9个关于本科教育质量的衡量指标建立综合评价模型,并进行进一步的分析与处理。主要涉及到数据的搜集和量化,综合评价模型的建立,指标的合理删除,关键指标的确定以及政策建议等五个方面。
2.1. 指标选取及量化处理
在查阅相关文献 [1] 以及百度百科 [2] [3] 的基础上,我们制定了如下的量化处理表1。



Table 1. Index quantization processing table
表1. 指标量化处理表
2.2. 数据初步分析
搜集到足够且有效的数据后 [4] 按照表1对数据做了一些量化处理,我们从原始数据的均值、方差、相关性分析以及作图等方面进行数据分析。

Table 2. Sum, mean and variance of data of each index number
表2. 各指标数数据的求和,均值和方差
由表2中的平均值和方差均可看出,各个指标的数据不在一个数量级,因此下面模型建立的时候要对这些数据进行无量纲化处理。


Table 3. The correlation coefficient matrix of the original data of each index
表3. 各指标原始数据的相关系数矩阵
由表3可知本科院校数量和招生人数,教学条件与利用和科研投入与产出,本科院校数量和双一流学科建设的相关性较强。
接下里,我们用Excel做出各市在不同指标的比较图,由于篇幅原因以及绘图简单,这里不再给出。而从图中可以看出,南京在本科院校数量上有绝对的优势,师资队伍和师资结构上有较大优势,并且其生师比例在13个市中也是比较低(也低越好),所以从这些数据直观上来看南京的本科教学质量在十三个市中是很高的。
假设进行主成分分析的指标变量有m个(这里,m = 9),分别为
,共有n个评价对象(这里n = 13),第i个评价对象的第j个指标的取值为aij,由此构成矩阵
。传统主成分分析的步骤为:
1) 对原始数据进行标准化处理,将各指标值aij转化为标准化指标值
,得到矩阵A*
其中,
,分别为第j个指标的样本均值和样本标准差。
2) 计算A*的样本协方差矩阵S。
3) 求出S的特征值为
,相应于
的正交化单位特征向量为
,则A*的第i个主成分为
,其中x为m维观测向量,即
,
。
4) 选择主成分,计算综合评价值。
a) 计算特征值
的信息贡献率bi。其中
(2.1)
b) 累积贡献率βk足够大(一般取βk = 0.85, 0.90, 0.95)时,则选择前k个主成分。其中
(2.2)
c) 最后计算出综合得分,并据此进行测评
(2.3)
2.3. 基于改进的主成分分析方法的评价模型的建立
下面针对传统主成分分析的两个误区进行改进 [5]。
2.3.1. 原始数据的预处理方法的改进1——原始数据的均值化
在实际应用主成分分析时,为了消除变量的量纲或数量级影响,需要对原始数据标准化,但同时也去除了各变量变异程度的差异信息。为了解决这一问题,有学者提出数据的均值化处理方法 [6],即用各指标的均值除相应的原始数据,令
(2.4)
于是得到均值化矩阵
。可以证明,均值化处理不改变各指标间的相关系数,均值化后的协方差矩阵不仅消除了指标量纲或数量级的影响,还能包含原始数据的全部信息,因此这里应用主成分分析时,使用均值化处理对原始数据进行预处理,也就是,将其中传统主成分分析的步骤里的矩阵A*换成均值化矩阵C即可。
2.3.2. 原始数据的预处理方法的改进2——数据的一致化处理
在9个指标中,存在两种类型的数据,一种是“正比型”,即数据的量化值越大,代表该市本科教育质量越好,比如教学条件与利用、双一流学科建设等指标,而另一种“反比型”则相反,量化值越大,说明教育质量越差,如生师比,科研投入与产出等指标。因此,为了方便对这两种数据同时进行主成分分析,我们将数据进行一致化处理,将全部数据都转化成“正比型”。
按照前面数据的量化处理方式,9个指标中,量化值是“反比型”的指标只有生师比。对于这个指标,令
(2.5)
其中,max(cj)是第j个指标中的最大值。而其余指标的数据不变,即
于是得到均值化矩阵C的一致化矩阵C*,实际处理时,将6.2.1中主成分分析的步骤里的矩阵C换成均值化矩阵C* 即可。
2.3.3. 综合评价方法的改进——熵值法
传统的主成分分析中,使用各主成分的方差贡献率作为权重,这显然带有主观成分 [7]。假设提取了r个主成分,经过计算各个样本在这r个主成分的得分,可得到具有n个样本,m项指标的主成分得分矩阵
。为得到更合适更客观的综合评价,可以采用熵值法进行改进。若某个变量的信息熵越小(大),就表明该变量的变异程度越大(小),在评价中的作用越大(小),权重也越大(小)。熵值法的计算步骤是:
a) 计算第j个主成分下第i个样本的比重:
, (2.6)
b) 计算第j个主成分的熵值:
, (2.7)
c) 计算第j个主成分的权重:
, (2.8)
d) 计算样本的综合值:
,最后按综合值对样本进行排序即可。
在第1步中,为防止矩阵中有的数据为负,可以将所有数据加上一个最小负数的绝对值, 这样平移不会改变结果,然后按平移后的矩阵进行上述的步骤。
至此,已经建立了基于改进的主成分分析方法的综合评价模型,下面应用该评价模型,对江苏省13个地级市的本科教育质量进行评估,并给出排名。
2.4. 模型应用——江苏省地级市的本科教育质量的评估与排名
按照前文中建立的改进的主成分分析模型,利用搜集的数据,分别计算常州、淮安、连云港、南京、南通、宿迁、苏州、泰州、无锡、徐州、盐城、扬州、镇江的本科教育质量的综合得分。
首先,利用Matlab软件对9个指标进行改进的主成分分析,相关系数矩阵的前几个特征根及其贡献率见表4。

Table 4. Improved principal component analysis results
表4. 改进主成分分析结果
可以看出,前4个特征根的累积贡献率就达到了94.5%以上,主成分分析效果很好。下面选取前4个主成分进行综合评价。前4个特征根对应的特征向量见表5。

Table 5. The eigenvectors corresponding to the first four principal components of the meanized variable
表5. 均值化变量的前4个主成分对应的特征向量
注:yi代表第i个主成分,xj代表示表1中第二指标列自上至下第j个指标。
接着按照上文对改进主成分分析方法的论述,可得到主成分得分矩阵D、熵值以及权重,见表6。


Table 6. Principal component score matrix
表6. 主成分得分矩阵
由此可构建基于改进的主成分分析方法的综合评价模型,即
(2.9)
将各城市的4个主成分值代入上式,可以得到各城市本科教育质量的综合评价值以及排序结果,见表7和图1。

Table 7. The comprehensive evaluation value and ranking result of undergraduate education quality in each city
表7. 各城市本科教育质量的综合评价值和排序结果
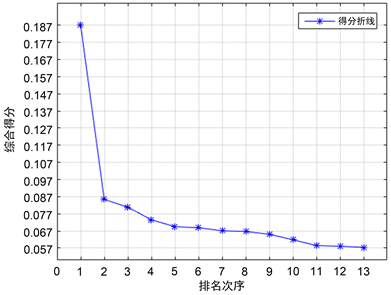
Figure 1. The comprehensive evaluation value and ranking result
图1. 各城市本科教育质量的综合评价值和排序结果图
从上面我们可以看出,南京市以0.1870的得分位列本科教学质量城市的第一位,且与排名第二的徐州市相比有较大领先优势,分差大于0.1,说明南京市的本科教学质量很好,而实际上也的确如此。从这里的理论排名和实际情况的比较中,我们也可以发现,基于改进的主成分分析方法建立的评级模型具有较好的合理性、准确性和客观性,将该模型作为评估城市本科教学质量的工具有其实际意义。
3. 基于相关性分析和权重的指标删除模型
3.1. 指标的初步删除
3.1.1. 指标间的相关性
若两个指标的相关性较大,则可以认为指标对本科教育质量评估的影响会产生较大的重叠部分,这无疑会在最终评测中加大重叠部分的影响,导致评估结果不太准确。而根据实际经验,题目中给出的9个指标或多或少是有着一些联系的,因此,我们计算这些指标的pearson相关系数,研究其相关性,且规定相关系数大于0.95的两个指标具有极强的相关性。
对于p, q两指标间的相关系数rp,q,计算公式为:
(3.1)
其中,n为13,
,
分别为p, q指标第i个城市均值化、一致化后的数据,其相关系数矩阵为:
由表8,得到本科院校数量和招生人数,教学条件与利用和科研投入与产出,本科院校数量和双一流学科建设的相关性极极强,分别为0.9614,0.9793,0.9908。
3.1.2. 指标的权重
我们可以根据式
(3.2)
算出每个指标对于本科教育质量评估模型的权重,结果如表9。

Table 9. The weight of each index to the comprehensive evaluation of urban undergraduate education quality
表9. 各个指标对城市本科教育质量综合评价的权重

Figure 2. The weight of each index to the comprehensive evaluation of urban undergraduate education quality
图2. 各个指标对城市本科教育质量综合评价的权重
如图2所示,可以看出,教学条件与利用的权重最小,仅为0.0160,而双一流学科建设权重较大,为0.1866。
3.1.3. 指标的初步删除
由表8和表9可以看出,双一流学科建设的权重较大,且与本科院校数量的相关性极大,所以重叠部分对最终综合得分的影响被严重放大,因此考虑去掉双一流学科建设这一指标;而教学条件与利用的权重极小,说明对最终得分的影响微乎其微,所以也可以去掉。下面我们利用改进的主成分分析对去掉这两个指标后的城市本科教学质量进行评估,以验证删除的合理性。评估结果如下:

Table 10. The ranking after deleting the double top discipline
表10. 删除双一流学科之后的排名

Table 11. The ranking after deleting teaching conditions and utilization
表11. 删除教学条件与利用之后的排名

Table 12. The ranking after deleting the construction and teaching condition and utilization of double top disciplines
表12. 删除双一流学科建设与教学条件与利用之后的排名
由表10和表11可知,删除双一流学科建设排名和教学条件与利用后,排名上基本上没有发生变化。
由表12可知,删除教学条件与利用与双一流学科建设后,排名有不小的变化。这说明可以单独删除两者中的任一个,但不能同时删去。由于上面的分析并未涉及到定量表示,所以删除的理由不是很充分,因此在下文,我们将进行比较精确的定量分析。
3.2. 指标删除与关键指标提取模型的建立
3.2.1. 虚拟控制城市的引入
至此,我们已经初步删除了一些对评价结果影响较小的指标,但准确性依然难以令人信服。下面,我们引入虚拟控制量,即虚拟控制城市来进一步定量研究各指标对于本科教育质量的影响大小。
令该控制城市的各项指标的数据为其余城市指标(均值化、一致化后的数据)的均值,即
(3.3)
其中,
为虚拟控制城市的第j个指标数据。
接着,将14个城市(包括虚拟控制城市)的指标的数据再次均值化,又根据虚拟控制城市数据的计算式,14个城市均值化后的数据不需要再进行一致化处理了。
数据处理完毕后,使用6.2建立的改进后的主成分分析评价模型对这14个城市的本科教育质量进行评估,设13个实际存在的地级市的得分向量为:
。
下面,通过改变虚拟控制城市各指标的数值,来定量研究每个指标对于最终评估得分的影响大小。具体操作方式为:分别将控制城市的指标
增加20%后重复上述的均值化和综合评价过程,从而得到调节虚拟控制城市第j个指标后产生的13个的地级市的综合得分向量:
。
3.2.2. 指标灵敏度的定量计算
这里,指标的灵敏度是指:指标对于综合评价得分的影响大小,也可以认为是普遍改善该指标后,城市间的本科教育质量差距能够减少的程度。灵敏度越大,说明影响越大,差距减少的程度越大。
得到综合得分Gj后,若直接通过排名变化来判断指标的灵敏度,一方面难以定量得到灵敏度的值,一方面由于排名变化较大以及一些信息会被隐藏起来,使得灵敏度的判断难度增大且准确度不高。因此,我们将指标调节前后的综合得分向量Gj与G0的欧氏距离作为该指标的灵敏度。基本步骤如下:
1) 综合得分的均值化处理
为了消除Gj间可能存在的量纲或数量级的影响,同时包含原始数据的全部信息,我们对改变第j个指标后的综合得分Gj进行均值化处理,公式如下:
(3.4)
其中,
, n = 13, m = 9。
2) 计算灵敏度
依照前面的分析,我们将第j个指标的灵敏度定义为改变虚拟控制城市的这个指标后得到的综合得分Gj与G0的欧氏距离Dj,即
(3.5)
其中,Dj可视为灵敏度,n = 13。
3.3. 指标删除与关键指标提取模型的求解
按模型的建立过程,我们首先插入一个虚拟控制城市,其各项指标的数据为表13:
其次,将14个城市的指标数据均值化,利用改进的主成分分析模型进行综合得分的计算,结果为表14:

Table 14. The comprehensive evaluation value and ranking result of undergraduate education quality in each city after inserting virtual city
表14. 插入虚拟城市后各城市本科教育质量的综合评价值和排序结果
接着,分别调节9个指标的值,通过改进的主成分分析模型得到综合得分Gj,再计算灵敏度Dj,这里以本科院校数量为例,使虚拟城市的本科院校数量增加20%,然后得到每个城市的得分如表15:

Table 15. The overall score of each city after changing the number of universities in the virtual controlled city
表15. 改变虚拟控制城市的本科院校数量后的各城市的综合得分
最后,结合表16中数据求得指标本科院校数量的灵敏度为0.0014。重复上述过程,可以分别得到9个指标的灵敏度。结果如表16:
由表16可知指标8即科研投入与产出的灵敏度远高于其余指标,所以科研投入与产出可作为关键指标。同时,指标双一流学科建设与教学条件与利用的灵敏度也较小说明上面对这些指标的删除是合理的。
4. 对江苏省本科教育的政策与建议
至此,本文的主要研究工作已经完成,在这一部分,我们将对本文成果进行总结,以此为基础,有针对性地给出能够有效提升江苏省本科教育质量的政策建议。以帮助江苏省的有关部门更好地做出相关决策。
4.1. 江苏省的本科教育现状
在基于改进的主成分分析方法的综合评价模型中,我们得到:南京市的综合得分要远远大于其他各市的得分,而其余几个地级市的差距均较小,并以徐州为首,苏州次之,最后是泰州,但徐州与泰州的得分也相差了0.03,大约是泰州总得分的3/5,所以这说明江苏省的本科教育质量在地域上是严重不均衡的。
在删除不必要指标以及选取关键指标的建模中,我们发现双一流学科建设对于综合得分的影响很小,可以从指标中删去,这说明双一流学科建设与其余指标有较大的重合,而且双一流学科建设目前并不是各市本科教育质量有差别的主要原因。在这一阶段的建模中,我们利用灵敏度找到了关键指标:科研投入与产出,通过观察各市在该指标的数据,可以发现,各市的差距还是很大的,南京市的得分尤其高,这也导致了在综合得分上体现出的较大差异。
4.2. 政策建议
根据江苏省本科教育质量地域分布不均的缺点,我们建议江苏省应该加大对南京以外的城市本科教育的重视程度以及政策支持。可以采取如下措施:
a) 在保持南京市本科教育优势的同时,鼓励南京市高校对省内其余各市的援助与指导,提高各市高校的科研投入与产出比,这样可以起到均衡教育资源的作用。
b) 江苏省有关部分应该加大对南京市以外各市高校的科研、校园建设等资金的投入,使其得以在科研经费、人才引进、学生培养等方面有更多的资本。
c) 江苏省各高校要重视双一流学科的建设,抓住双一流学科建设对本科教育质量影响较小的机会,努力建设好双一流学科。双一流学科是国家重点关注对象,所以日后的影响必然会增大。因此未来本科教育质量的评估也会有所改变。
以上便是我们对江苏本科教育质量现状的分析以及据此给出的几点建议,希望这些建议能够对江苏省本科教育的进一步提高提供一些有用的思路和帮助。
附录
指标数据表