土钉墙支护及其应力特征数值模拟分析——以长沙中建梅溪湖项目基坑支护为例

Numerical Simulation Analysis of Soil Nailing Wall Support and Its Stress Characteristics—Taking the Foundation Pit Support of Meixi Lake Project of Changsha Zhongjian as an Example

摘要: 本文以长沙中建梅溪一号(3B地块)基坑工程为例，通过前期的地质调查、多方案论证，确定了初步的土钉墙支护结构和放坡挂网素喷的基坑支护方案，应用FLAC3D对支护方案模拟，模拟分析了采用土钉墙支护条件下，基坑开挖过程中基坑土体的应力场分布规律、支护结构受力状况，模拟结果显示：1) 从土钉受力情况来看，土钉轴力基本为拉力。同时，随着开挖工程的开展，土钉受力情况是随之而发生变化的，数值模拟结果显示，开挖过程中，土钉所承受的最大轴力为5.2 t。2) 土钉在长度方向上轴力分布遵循“中性点”原则，即中间数值大、两边数值小。最大轴力位置在潜在滑移面处。靠近坡面土钉段的轴力大于土钉深部段轴力这说明，土钉除了承受土体变形后施加的动力外，还受到喷射混凝土面层施加在土钉上的抗拔力作用。3) 随着开挖的进行，土钉受力逐渐增大。这主要是由于开挖深度增加，基坑边坡土体变形增加，将土体的位移力和土体膨胀力传递给土钉所致。

Abstract: In this paper, taking the foundation pit project of No. 1 Meixi (3b block) of Changsha Zhongjian as an example, through the preliminary geological investigation and multi scheme demonstration, the preliminary soil nailing wall supporting structure and the foundation pit supporting scheme of sloping hanging net and plain spraying are determined. The FLAC3D is used to simulate the supporting scheme, and the stress field distribution rule and supporting structure of the foundation pit soil during the excavation are simulated and analyzed. The results show that: 1) The axial force of soil nail is tensile force. At the same time, with the development of excavation engineering, the stress of soil nails changes accordingly. The numerical simulation results show that the maximum axial force of soil nails is 5.2 t. 2) The axial force distribution of soil nail in the length direction follows the principle of “neutral point”, that is, the middle value is large and the two sides value is small. The maximum axial force is located at the potential slip surface. The axial force of the soil nail near the slope is greater than that of the deep part of the soil nail, which indicates that the soil nail is not only subjected to the force exerted by the deformation of the soil, but also to the pull-out force exerted by the shotcrete surface on the soil nail. 3) With the progress of excavation, the stress of soil nail increases gradually. This is mainly due to the increase of excavation depth and soil deformation of foundation pit slope, which transfers the displacement force and expansion force of soil to soil nails.

1. 引言

土钉是一种基于新奥隧道法原理发展起的一种基坑支护技术 [1] - [8]。新奥隧道法(The New Austrian Tunneling Method)最早见于六十年代初期，到六十年代中期，随着经验施工观测资料的积累与施工经验的丰富，陆续将此法从硬质岩层推广到含软岩层、粉土、砾石和砂石的隧道施工当中 [9] [10]。随着计算机技术的发展及数学理论的不断提升，有关土钉支护的研究方法主要有以下四种：1) 试验方法 [11]；2) 极限平衡法 [12] [13] [14]；3) 有限元法 [15]；4) 有限差分法 [16] [17] [18]。试验方法的开展大量的资金投入，对于一般的科研机构由于资金不足而不能够系统的展开试验研究，尤其是大型足尺试验的开展更为不现实，而对于生产单位则为了追求经济效益，一般也不愿意将资金投入到此方面。极限平衡分析法在土钉有关变形信息与内力精确分布两大方面存在一定的不足，从而难以全面评估土钉支护的工作性能及安全性。计算机技术的发展，既节约了大量的资金，又能够通过计算获得土钉支护内力、变形等较全面详细的数据分析，因此通过计算机数值模拟可以为基坑工程的设计和施工提供指导性依据 [19] [20] [21] [22] [23]。而利用有限元开发的大型通用软件ANSYS和利用有限差分原理开发的FLAC3D软件相比，后者运算速度快，是专门的岩土模拟程序，针对性强 [24] [25] [26]。

本文长沙中建梅溪一号(3B地块)基坑支护方案为例，利用FLAC3D程序对其位移场及稳定性进行数值模拟分析，并与现场实测数据结果进行比较，以期得到一些有参考意义的结论，为以后本地区及相似工程地质条件的基坑支护研究工作提供一定的参考。

2. 地质条件概述

2.1. 场地地层条件

场地内共涉及11层土，分别为第1层：杂填土(Q_4-3^m1)；第2层：新近沉积粉土(Q_4-3^a1)；第3层：新近沉积粉质粘土夹粉土(Q_4-3^a1)；第4层：新近沉积粉质粘土(Q_4-3^a1)；第5层(Q_4-2¹)：粉土；第6层：粉质粘土(Q_4-2¹)；第7层：粉土(Q_4-2¹)；第8层：粉质粘土(Q_4-2¹)；第8夹层：粉土(Q_4-2¹)；第9层：粉土(Q_4-2¹)；10-1层：粉砂(Q_4-1^a1)；第10层：细砂(Q_4-1^a1)；第11层：粉质粘土(Q₃^a1)。

2.2. 场地水文地质条件

前期工程勘查资料表明，勘探深度范围内场地的地下水可分为两层，上层为潜水，下部为承压水，两者被相对隔水层第8层粉质粘土隔开。场地内自然水位约为地表下1.5 m。根据规范要求以及周边工程施工经验，建议上部潜水含水层的综合渗透系数取K = 0.5 m/d，下部承压水含水层的综合渗透系数取K = 8.0 m/d。

2.3. 主要土层物理力学指标

场地内各主要土层的物理力学指标见表1。

Table 1. Physical and mechanical indicators of major soil layers

表1. 主要土层物理力学指标

3. 基坑支护设计

本工程的基坑支护对三个1-1’、2-2’、3-3’剖面(图1，图2，图3)采用土钉支护的方案，对4-4’剖面采用放坡挂网素喷的支护方式，土钉支护方案的支护参数见表2，表3，表4；素喷坡面的设计参数见图4。

4. 应力–应变规律

当各个三角形内的应变张量确定以后，然后初始设定的本构规律计算相应的应力。在此之前，需要对原有的应力进行两个方面的修正：1) 转动应力作修正；2) 扣除孔隙压力。应变与应力间的本构关系给成增量形式：

$\Delta {\sigma }_{ij}=f\left(\Delta {\mathcal{l}}_{ij},{\sigma }_{ij},\cdots \right)$ (1)

式中： $\Delta {\sigma }_{ij}$ ——应力增量张量， $i,j=1,2$ ；

$f\left(\right)$ ——包含有增量应变，现存总应力状态，材料常数等的本构方程。

Figure 1. Diagram of 1-1’ profile

图1. 剖面1-1’示意图

Figure 2. Diagram of 2-2’ profile

图2. 剖面2-2’示意图

Figure 3. Diagram of 3-3’ profile

图3. 剖面3-3’示意图

Table 2. Soil nailing support parameters of 1-1’ profile

表2. 剖面1-1’土钉支护参数

Table 3. Soil nailing support parameters of 2-2’ profile

表3. 剖面2-2’土钉支护参数

Table 4. Soil nailing support parameters of 3-3’ profile

表4. 剖面3-3’土钉支护参数

4.1. 网点处不平衡力的确定

一旦四边形域内的应力张量已经求得，便可以用它来计算各网点处的不平衡力。重写运动方程式 [24] [27]：

$p\left[\frac{\partial {\stackrel{\dot{}}{u}}_i}{\partial \tau }\right]=\frac{\partial {\sigma }_{ij}}{\partial x_j}+p{g}_i$ (2)

其结果为

$p\left[\frac{\partial {\stackrel{\dot{}}{u}}_i}{\partial \tau }\right]=\frac{1}{A}{\displaystyle \sum {\sigma }_{ij}{\epsilon }_{jk}\Delta x_k}+p{g}_i$ (3)

或

$\frac{\partial {\stackrel{\dot{}}{u}}_i}{\partial \tau }=\frac{F_i}{m}+g_i$

式中：

$F_i={\displaystyle \sum {\sigma }_{ij}{\epsilon }_{jk}\Delta x_k},m=pA$

因此网点力变为：

$F_i={\sigma }_{ij}^a{\epsilon }_{jk}\left(x_k^{\left(1\right)}-x_k^{\left(4\right)}\right)+{\sigma }_{ij}^b{\epsilon }_{jk}\left(x_k^{\left(2\right)}-x_k^{\left(1\right)}\right)+{\sigma }_{ij}^c{\epsilon }_{jk}\left(x_k^{\left(3\right)}-x_k^{\left(2\right)}\right)+{\sigma }_{ij}^d{\epsilon }_{jk}\left(x_k^{\left(4\right)}-x_k^{\left(3\right)}\right)$ (4)

这个力在所有应力和坐标，在时刻t，t + Δt等时都是已知的。在下一个半时间步长时的网点速度为：

${\stackrel{\dot{}}{u}}_i\left(t+\frac{\Delta t}{2}\right)={\stackrel{\dot{}}{u}}_i\left(t-\frac{\Delta t}{2}\right)+\frac{F_i^t}{m}\Delta t+g_i$ (5)

应该指出，如果域中出现任何一个错误，那么出现错误的域中的各项将由式(4)中直接省略掉。

如果模拟过程中，选择尺度较大的应变模型，则把修正以后的网格坐标用于式(5)的，求得各新速度：

$x_i^{\left(t+\Delta t\right)}=x_i^{\left(t\right)}+{\stackrel{\dot{}}{u}}_i^{\left(t+\frac{\Delta t}{2}\right)}\Delta t$ (6)

4.2. 应力转动修正项

当利用代码中的大应变逻辑时，由于物体的转动，必须修正应力。应力的正规转动方程式为：

${\bar{\sigma }}_{ij}={\sigma }_{\alpha \beta }{J}_{i\alpha }{J}_{j\beta }$ (7)

$J_{ij}=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$ (二维)

式中： ${\bar{\sigma }}_{ij}$ ——大应变转动时修正了的应力张量。

当角度 $\Delta \theta$ 非常小的条件下，因为 $\cos \theta \approx 1,\sin \theta \approx \Delta \theta$，则

$J_{ij}=\left[\begin{array}{cc}1& \Delta \theta \\ -\Delta \theta & 1\end{array}\right]$ (二维)

因此，

$\begin{array}{l}{\bar{\sigma }}_{11}={\sigma }_{11}{J}_{11}{J}_{11}+{\sigma }_{21}{J}_{12}{J}_{11}+{\sigma }_{12}{J}_{11}{J}_{12}+{\sigma }_{22}{J}_{12}{J}_{12}\\ ={\sigma }_{11}+{\sigma }_{21}\Delta \theta +{\sigma }_{12}\Delta \theta +{\sigma }_{22}\Delta {\theta }^2\\ \Delta {\sigma }_{11}=2{\sigma }_{12}\Delta \theta \left(因为{\sigma }_{21}={\sigma }_{12},\Delta \theta 很小时,\Delta {\theta }^2=0\right)\end{array}$ (8)

特殊条件下， ${\sigma }_{11}$ 的修正项为

$\Delta {\sigma }_{11}=-2{\sigma }_{12}\Delta \theta$ (9)

同理，有

$\begin{array}{c}{\bar{\sigma }}_{22}={\sigma }_{11}{J}_{21}{J}_{21}+{\sigma }_{21}{J}_{22}{J}_{21}+{\sigma }_{12}{J}_{21}{J}_{22}+{\sigma }_{22}{J}_{22}{J}_{22}\\ ={\sigma }_{11}\Delta {\theta }^2-{\sigma }_{21}\Delta \theta -{\sigma }_{12}\Delta \theta +{\sigma }_{22}^2\\ ={\sigma }_{22}-2{\sigma }_{12}\Delta \theta +{\sigma }_{11}\Delta {\theta }^2\end{array}$ (10)

反号并略去 $\Delta {\theta }^2$ 项后，有

$\Delta {\sigma }_{22}=-2{\sigma }_{12}\Delta \theta$ (11)

还有

$\begin{array}{c}{\bar{\sigma }}_{12}={\sigma }_{11}{J}_{11}{J}_{21}+{\sigma }_{21}{J}_{12}{J}_{21}+{\sigma }_{12}{J}_{11}{J}_{22}+{\sigma }_{22}{J}_{12}{J}_{22}\\ =-{\sigma }_{11}\Delta \theta -{\sigma }_{21}\Delta {\theta }^2+{\sigma }_{12}+{\sigma }_{22}\Delta \theta \end{array}$ (12)

$\Delta {\sigma }_{12}=\left({\sigma }_{11}-{\sigma }_{22}\right)\Delta \theta$ (13)

当采用大应变逻辑时，把这些修正项加到各应力中。

5. 基坑模型及参数设置

5.1. 模拟边界设置

本基坑位于长沙市岳麓区梅溪湖片区境内，南邻梅溪湖路，东邻E2路，场地交通便利，地理位置优越。实际基坑为长方形，基坑外轴线面积约102 × 371.9 m²，南北侧开挖深度为地表下6 m，中部为8 m。根据场地工程地质条件，基坑支护方案拟采用以下两种形式：1) 土钉墙支护；2) 放坡挂网素喷支护方案。据工程经验与现场实际情况，本次数值模拟模型尺寸设置为30 m × 20 m × 20 m。

5.2. 模型参数设置

模型中岩土物理力学参数按基坑支护方案设计中参数取值。

5.3. 计算模型

本次共建立三个力学模型，分别是工况一基坑开挖6 m (设计方案剖面2，位于基坑北侧)、工况二基坑开挖深8 m (设计方案剖面1，位于基坑东侧)、工况三基坑开挖深8 m (设计方案剖面3，位于基坑西侧)。各剖面数值模拟模型图分别见图4~6。

Figure 4. Section 2 model diagram

图4. 剖面二模型图

Figure 5. Section 1 model diagram

图5. 剖面一模型图

Figure 6. Section 3 model diagram

图6. 剖面三模型图

5.4. 支护结构的模拟

土钉采用FLAC3D中的锚索结构(cable)，喷射混凝土用壳结构(shell-type)。土钉及混凝土层面的参数如表5和表6所示。

Table 5. Soil nail material parameters

表5. 土钉材料参数

Table 6. Concrete parameters

表6. 混凝土参数

6. 数值模拟结果及分析

6.1. 土层初始应力状态模拟

在长期自重应力作用下，基坑在开挖施工前，施工区的地层土体已经处于稳定状态。所以在模型过程中，需要对模型进行应力初始化。开挖计算前，位移场和速度场需要清零，以避免出现误差。见图7所示。

从模拟结果来看，研究区基坑深度范围内土体垂直应力呈现由上至下呈递增分布的规律，在地表附近约为−0.05 MPa (负号表示为压力)，直至基坑深处时，其数值大约为−0.38 MPa。模拟结果与现场土层的应力分布状态基本吻合。

6.2. 土钉轴力分析

1) 剖面1土钉轴力(图8~13)

Figure 7. Stress initialization cloud chart

图7. 应力初始化云图

Figure 8. Excavation 1.5 m soil nail axis diagram

图8. 开挖1.5 m土钉轴力图

Figure 9. Excavation 3 m soil nail axis diagram

图9. 开挖3 m土钉轴力图

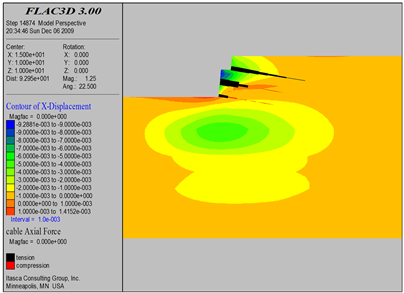
Figure 10. Excavation 4.5 m soil nail axis diagram

图10. 开挖4.5 m土钉轴力图

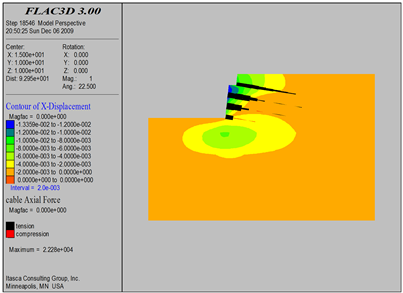
Figure 11. Excavation 6 m soil nail axis diagram

图11. 开挖6 m土钉轴力图

Figure 12. Excavation 8 m soil nail axis diagram

图12. 开挖8 m土钉轴力图

Figure 13. Excavation after stabilization of soil nail axial force curve

图13. 开挖稳定后土钉轴力曲线

2) 剖面2土钉轴力(图14~18)

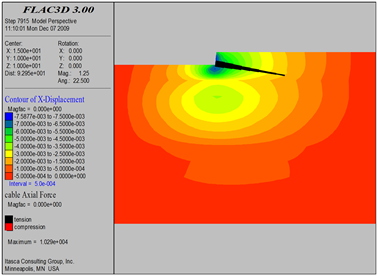
Figure 14. Excavation 1.5 m soil nail axis diagram

图14. 开挖1.5 m土钉轴力图

Figure 15. Excavation 3 m soil nail axis diagram

图15. 开挖3 m土钉轴力图

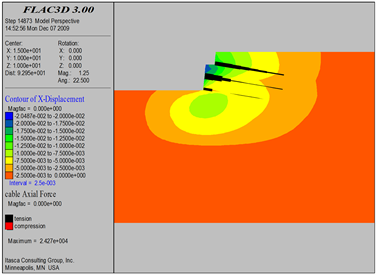
Figure 16. Excavation 4.5 m soil nail axis diagram

图16. 开挖4.5 m土钉轴力图

Figure 17. Excavation 6 m soil nail axis diagram

图17. 开挖6 m土钉轴力图

Figure 18. Axial force curve of soil nail after excavation stability

图18. 开挖稳定后土钉轴力曲线

3) 剖面3土钉轴力(图19~24)

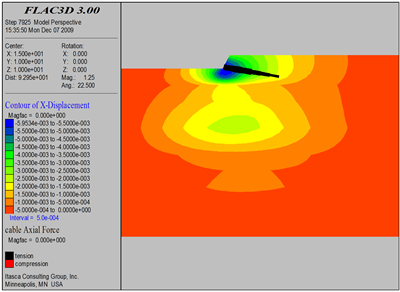
Figure 19. Excavation 1.5 m soil nail axis diagram

图19. 开挖1.5 m土钉轴力图

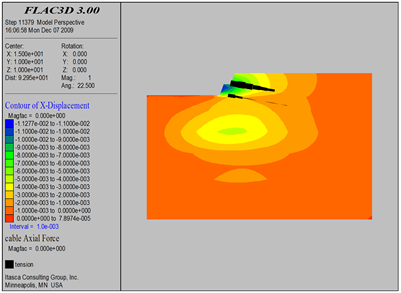
Figure 20. Excavation 3 m soil nail axis diagram

图20. 开挖3 m土钉轴力图

Figure 21. Excavation 4.5 m soil nail axis diagram

图21. 开挖4.5 m土钉轴力图

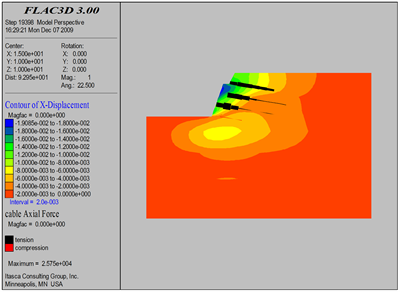
Figure 22. Excavation 6 m soil nail axis diagram

图22. 开挖6 m土钉轴力图

Figure 23. Excavation 8 m soil nail axis diagram

图23. 开挖8 m土钉轴力图

Figure 24. Axial force curve of soil nails after excavation stability

图24. 开挖稳定后土钉轴力曲线

对基坑开挖过程中土钉受力进行了实时监测如图8~24所示，得出如下结论：

1) 从土钉受力情况来看，土钉轴力基本为拉力。同时，随着开挖工程的开展，土钉受力情况是随之而发生变化的，数值模拟结果显示，开挖过程中，土钉所承受的最大轴力为5.2 t。

2) 土钉在长度方向上轴力分布遵循“中性点”原则，即中间数值大、两边数值小。最大轴力位置在潜在滑移面处。靠近坡面土钉段的轴力大于土钉深部段轴力这说明，土钉除了承受土体变形后施加的动力外，还受到喷射混凝土面层施加在土钉上的抗拔力作用。

3) 随着开挖的进行，土钉受力逐渐增大。这主要是由于开挖深度增加，基坑边坡土体变形增加，将土体的位移力和土体膨胀力传递给土钉所致。

7. 结论

1) 从土钉受力情况来看，土钉轴力基本为拉力。数值模拟结果显示，开挖过程中土钉所承受的最大轴力为5.2 t。

2) 土钉在长度方向上轴力分布遵循“中性点”原则，即中间数值大、两边数值小。

3) 随着开挖的进行，土钉受力逐渐增大。