1. 引言
我国是煤炭生产和消费大国,历年来,煤炭消费占能源消费总量的59%以上。“富煤、贫油、少气”是我国的能源现状,煤炭是我国的主体能源和重要工业原料,在能源生产和消费中处于主导地位,在我国国民经济中具有重要的战略地位。党的十八大以来,煤炭供给侧结构性改革取得显著进展,煤炭行业经济效益显著提高。我国经济发展对煤炭高度依赖,煤炭价格波动对我国经济的影响较为深远 [1],研究我国煤炭价格指数的波动具有重要意义。
我国煤炭价格波动的研究一直是时间序列统计分析的热点。刘畅通过构建一个基于总供给、经济需求、库存需求、运输量和特异性冲击的五变量SVAR模型对2003~2018年中国煤炭价格指数的波动因素进行深入分析,认为中国煤炭价格是多种因素共同作用的结果,煤炭供给冲击和经济需求冲击分别对煤炭价格产生负向和正向影响 [2]。邹绍辉、张甜以秦皇岛大同优混煤2003年3月~2017年5月现货价格为实证研究对象,分别采用普遍最小二乘法和GARCH模型对煤炭价格时序进行拟合,建立拟合效果较优的GARCH(1,1)模型,得出外部冲击会加剧煤炭价格波动,煤炭价格时间序列具备长期记忆性,煤炭价格波动的持续性较强等结论 [3]。张艳芹从金融要素和煤炭价格波动关系的角度对我国煤炭价格的波动展开研究,从需求冲击、供给冲击和替代效应三个方面,运用定性和定量分析的分析方法,使用协整方程以及误差修正模型从静态角度研究了影响我国煤炭价格波动的金融因素 [4]。张建英选取2009年~2012年煤炭价格和对其产生影响的相关月度数据,运用单位根检验、协整检验、Granger因果检验及VAR模型对影响我国煤炭价格的因素进行了研究,指出煤炭价格主要受自身波动的影响,其次受大宗商品价格、宏观经济景气指数和煤炭产量影响 [5]。王文琦运用协整分析构建煤炭价格的Var模型,从宏观因素、行业因素、国际市场因素、微观因素四个层次对新常态下中国煤炭价格波动影响因素进行了研究 [6]。
2006年开始我国煤炭价格全面开放,由市场进行定价,2012年开始煤炭供给侧改革,煤炭行业经济效益显著提高。本文以2006年1月开始的中国煤炭价格指数为研究对象,对2012年1月以后的中国煤炭价格指数进行着重分析。
中国煤炭价格指数(简称CCPI)由中国煤炭工业协设会从2006年1月1日开始发布,以周作为发布周期。该价格指数通过了中国煤炭工业协会和中国设煤炭运销协会组织的设国内外专家设的充分论证 [7]。
2. 描述性统计
本文选取2006年1月~2020年5月每月对应周次相应煤炭价格指数(全国综合)的平均值作为研究对象(数据来自wind数据库)。图1为我国煤炭价格指数的时序图,可以看出,在2008年之前我国煤炭价格呈现小幅上升,2008年迅速上升并达到最高点,之后价格回落,煤炭价格整体出现疲软。从图中的变动趋势来看,煤炭价格具有明显的随机波动趋势。我国煤炭价格指数的统计特征:平均值为153.67,标准差为27.41,最高值出现在2008年8月为220.4,2008年以后最低值出现在2016年1月为124.75,最高峰出现在2011年11月为203。煤炭价格指数的时间序列峰度为2.629503 < 3,偏度为−0.125018 < 0,说明煤炭价格指数时间序列呈现非正太分布,在1%的显著性水平下,JB统计量也拒绝煤炭价格指数时间序列服从正态分布的假设。
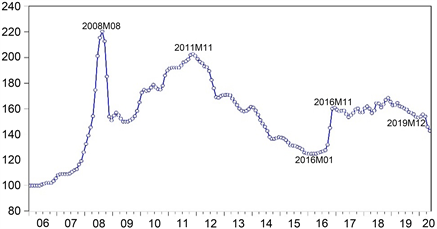
Figure 1. Time series chart of CCPI
图1. 我国煤炭价格指数时序图
图2为通过X-11方法提取的我国煤炭价格指数的季节指数:2012年之前煤炭价格季节指数波峰出现在6月份,波谷出现在11月份;从2012年开始煤炭价格季节指数波峰出现在1,2月份,波谷出现在5,8月份。季节指数波动最大值出现在06年,差距皆为0.062,最小值出现在2011年,差距为0.03,近5年来季节指数波动稳定在0.33。
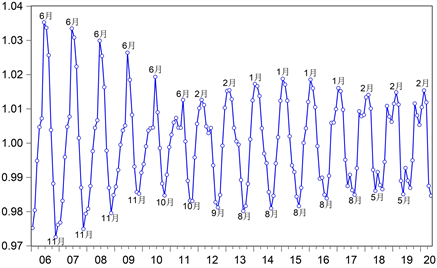
Figure 2. Seasonal factors of CCPI
图2. 我国煤炭价格指数季节指数
序列存在季节变化,且季节效应的大小随着时间连续变化,近7年的季节波动指数较稳定,这里截取2012年1月至2019年6月我国煤炭价格指数数据,通过Holt-winters三参数乘法指数平滑法对我国煤炭价格指数做出预测,平滑系数α = 1.00,β = 0.29,γ = 0.00,预测结果如图3,2020年下半年价格持续下降,9月份后下降放缓。
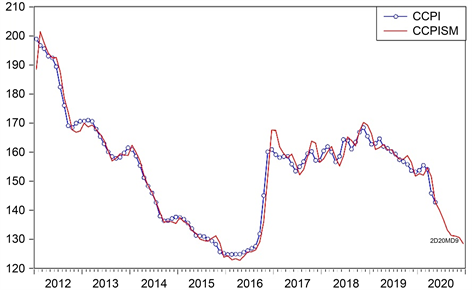
Figure 3. Exponential smoothing forecast result of CCPI
图3. 我国煤炭价格指数光滑预测结果
3. 基于ARIMA-ARCH模型的研究
基于2012年1月~2020年5月我国煤炭价格指数数据进行ARIMA-ARCH建模 [8]。
1) 时序图、自相关图和单位根检验都显示该序列为非平稳序列,对原时序进行一阶差分处理后,经过单位根及白噪声检验,对应时序为平稳白噪声序列,即原时序为1阶单整非纯随机时序。
2) 对差分后时序进行ARMA模型建模,根据样本自相关和偏自相关系数进行模型定阶,结合AIC、SBC信息准则,最终选定ARIMA(0,1,2)模型,拟合结果如下:
.
该模型都通过了回归系数显著性检验和残差白噪声检验,且AIC = 4.54,SC = 4.62,DW = 1.98。
3) 基于ARCH-LM检验、ARCH-QLB检验和残差正态性检验对上述中两个均值方程的残差平方进行ARCH效应检验,结果显示残差序列都具有显著条件异方差性,经过一系列尝试,最终对ARIMA(3,1,0)模型残差序列拟合ARCH(1)-正态分布模型,拟合结果如下:
且AIC = 4.27,SC = 4.39,DW = 1.86,所有系数都通过了显著性检验。
4) 经过ARCH-QLB检验,ARCH(1)模型标准化残差平方不再存在ARCH效应,说明我国煤炭价格指数序列均值方程加入ARCH模型后,消除了残差序列中存在的自回归条件异方差性,ARCH(1)模型已将残差序列平方的相关性提取完全。
从以上拟合结果可以看到:① ARCH系数通过显著性检验,说明均值方程的残差确实存在条件异方差性;GARCH模型相对均值模型,AIC、SBC显著减小,说明ARCH模型较ARIMA模型对我国煤炭价格指数时序的拟合效果更好,考虑条件异方差与不考虑条件异方差的模型预测结果见图4,通过对比可明显发现,考虑条件异方差情形下的模型预测结果更为精确,2020年我国煤炭价格最高值将出现在7月。② ARCH系数为0.56,GARCH系数为0,说明不存在非对称效应,好消息和坏消息对波动性的冲击一样大;同时说明我国煤炭价格受外在事件或政策影响时反应强烈,但对系统内部造成的影响反应可忽略。这些结论与张艳芹 [9]、邹绍辉 [3] 不一致。
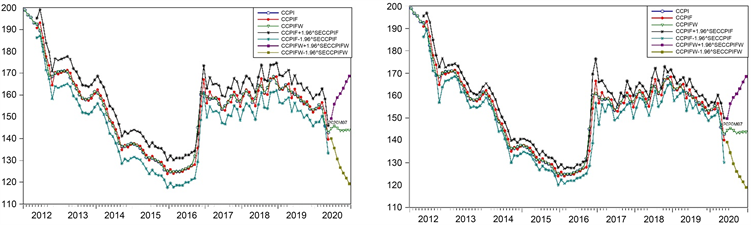
Figure 4. Forecast result of ARIMA model (left) and ARCH model (right)
图4. 不考虑异方差(左)和考虑条件异方差(右)下的预测结果
4. 基于协整–误差修正模型的研究
煤炭作为一种特殊商品,其价格必然受多种因素影响。本文欲建立我国煤炭价格指数与国际WTI原油价格、我国原煤产量、原煤销售量、原煤进口量、原煤出口量、火力发电量、钢材产量、居民消费价格指数cpi、零售物价指数rpi之间的回归模型以期量化它们之间的动态关系。通过时序图可确定我国煤炭价格指数只与WTI石油价格存在明显同变关系所以,这里选用WTI原油价格作为影响煤炭价格的因素进行实证分析。
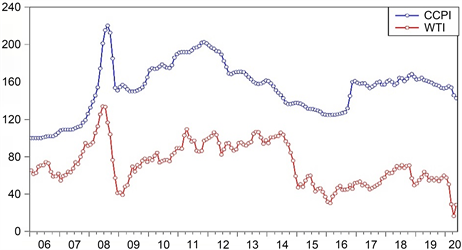
Figure 5. Time series chart of CCPI and WTI
图5. 我国煤炭价格指数与WTI原油价格时序图
1) 通过图5可确定我国煤炭价格指数
与WTI原油价格
存在明显的同变关系,接下来对两者之间协整关系的存在性进行检验,并进一步构建误差修正模型。
2) 通过单位根检验可知我国煤炭价格指数
与WTI原油价格
皆为1阶单整非白噪声序列。结果见表1和表2。构造我国煤炭价格指数序列
与WTI原油价格序列
的回归模型:
,
该模型回归系数通过了显著性检验。
3) 对以上模型残差序列进行单位根检验,检验结果见表3:可判定残差具有平稳性,进而我国煤炭价格指数序列
与WTI原油价格序列
之间的协整关系成立。

Table 1. Correlogram of d (WTI)
表1. WTI原油价格一阶差分序列非白噪声检验结果

Table 2. Augmented dickey-fuller unit root test on d (WTI)
表2. WTI原油价格一阶差分序列单位根检验

Table 3. Augmented dickey-fuller unit root test on model residuals
表3. 回归模型残差序列的单位根检验结
4) 协整关系的确立,说明我国煤炭价格指数与WTI原油价格之间存在着长期稳定的均衡关系,这是从整体上来说,但在时序观测的局部时间段内,可能会在局部时间段内单整时序之间距离的比较近或比较远,不再同步,意味着这种均衡关系有可能被打破。为了测度这种局部不均衡状态,进一步构建误差修正模型:
,其中
。
误差修正模型显示,WTI原油价格指数当期波动对我国煤炭价格指数当期波动有显著影响,上期误差对当期波动的影响也高度显著;同时,从回归系数的绝对值大小可以看出WTI原油价格指数的当期波动对我国煤炭价格指数的当期波动调整幅度很大,WTI原油价格指数每增加1个单位,我国煤炭价格指数便会增加0.28个单位,上期误差对当期我国煤炭价格指数的当期波动调整幅度较小,单位调整比例为−0.04。
5. 总结
本文基于指数平滑法、ARIMA-ARCH模型、协整–误差修正模型多个时间序列分析方法对我国煤炭价格指数进行了系统研究。
1) 基于指数平滑方法,可以发现我国煤炭价格指数周期性的表现在2012年前后是不相同的,且最近7年周期性趋于稳定。运用Holt-Winters三参数乘法指数平滑法,可以预测2020年我国煤炭价格持续走低。
2) 基于ARIMA-ARCH模型结果,ARCH系统通过了显著性检验,说明均值方程的残差平方确实存在条件异方差性;ARCH模型相对于均值模型,AIC,SC都显著减小,说明ARCH模型较均值方程对应模型对我国煤炭价格指数时序的拟合效果更好,考虑条件异方差的模型预测结果明显比不考虑异方差的模型预测结果更为精确。两个预测结果均显示,2020年我国煤炭价格最高值将出现在7月。ARCH系数大于GARCH系数说明我国煤炭价格受外在事件或政策影响反应强烈,但对系统内部造成的影响可忽略,且不存在非对称效应,好消息和坏消息对波动性的冲击一样大。
3) 基于协整–误差修正模型结果,可以看出WTI原油价格指数当期波动对我国煤炭价格指数当期波动有显著影响,上期误差对当期波动的影响也高度显著;同时WTI原油价格指数的当期波动对我国煤炭价格指数的当期波动调整幅度很大,上期误差对当期我国煤炭价格指数的当期波动调整幅度较小。
基金项目
本文受中国矿业大学(北京)“课程思政”示范课程建设项目:时间序列分析的支持。
NOTES
*通讯作者。