具有逃逸阶段的HIV模型的稳定性研究

Study on the Stability of HIV Model with Escape Stage

摘要: HIV病毒动力学的数学模型用于描述病毒和寄主细胞之间是相互作用，研究人类免疫缺陷病毒(HIV)病毒动态变化的数学模型。这个模型的一个主要特征是，包含一个感染单元的逃逸阶段，代表感染的T细胞尚未开始产生新病毒的阶段，利用分数阶微分方程稳定性理论，建立一个由四个非线性常微分方程组成的模型。首先，考虑模型只有在非负解和正解存在的情况下才有意义，讨论分数阶常微分方程正解的存在性问题。其次，将分数阶引入HIV感染CD4⁺ T细胞的模型，通过分析，得到方程的正解的存在性和平衡点渐近稳定性条件。最后借助MATLAB进行数值模拟，提供了一个更加完整的系统动力学，同时也验证模型结果是否正确。

Abstract: A mathematical model of HIV dynamics is used to describe the interaction between the virus and the host cell, study the mathematical model of dynamic change of human immunodeficiency virus (HIV) virus. One of the main features of this model is that it contains an escape phase of the infection unit, a phase in which infected T cells have not yet begun to produce new viruses, using the fractional differential equation stability theory, build a model of four Linear differential equation. First, we consider that the model is meaningful only if non-negative solutions and positive solutions exist, and discuss the existence of fractional ordinary differential equation positive solutions. Secondly, the fractional order is introduced into the model of HIV infected CD4⁺ T cells. Through analysis, the existence of positive solution and the asymptotic stability of equilibrium point are obtained. Finally, MATLAB is used to carry out numerical simulation to provide a more complete System dynamics, and also verify the correctness of the model results.

1. 引言

1.1. 研究背景

艾滋病是危害人类身体的一种慢性传染病，它逐步毁坏人体的免疫系统，使患者受到一系列威胁到生命的传染病、神经系统疾病等。艾滋病的传播 [1] 可以理解为一定体量的体液交换。在体内的流动的液体甚至能在分泌物中进行传播。其需要满足三个条件：液体交换主要是身上有开放性伤口，同时也可能是和HIV患者发生有液体交换的行为，包括性行为、输血、纹身等；液体交换必须达到一定的量，才能感染。人们熟知的性、血液、母婴传播其根本的原因就是：同时满足了体液交换量大、时间够长、交换环境够隐秘三个条件。但是若在没有及时采取有效的干预措施的前提下，将会有15%~30%的HIV，也就是一种能攻击人体免疫系统的病毒所引起慢性传染病，使孕妇不管是在分娩前还是分娩期间甚至能通过产后母乳喂养的形式将艾滋病传染给下一代 [2]。

1.2. 国内外研究成果

2007年Rong等人研究了HIV-1感染基本模型的推广：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=b-\beta x\left(t\right)v\left(t\right)-dx\left(t\right)+\delta w\left(t\right),\\ \frac{\text{d}y}{\text{d}t}=kw\left(t\right)-\mu y\left(t\right),\\ \frac{\text{d}w}{\text{d}t}=\beta x\left(t\right)v\left(t\right)-\left(\delta +\eta +k\right)w\left(t\right),\\ \frac{\text{d}v}{\text{d}t}=\sigma y\left(t\right)-\gamma v\left(t\right),\end{array}$ (1)

模型(1)中 $x\left(t\right)$、 $y\left(t\right)$、 $w\left(t\right)$ 和 $v\left(t\right)$ 分别表示是未感染CD4⁺ T细胞、生产性感染细胞和游离病毒

在t时刻的密度。b表示未受感染的细胞以速度b产生， $\beta x\left(t\right)v\left(t\right)$ 表示游离的病毒的速率，k表示非生产性感染细胞的速率以k的速率生产性感染细胞。

近年来，分数阶微积分是微积分其中的一类，其主要研究任意阶积分和导数的理论和应用，其概念最早是由Leiblilz在1695年提出。分数阶模型逐渐切合实际情况，能进行更深入的研究。

1.2. 模型的建立及其意义

我们考虑了Rong等人 [3] 中介绍的HIV-1病毒动力学的数学模型(1)。其模型只能反映随着时间变化的流行病学和人口学过程。但在实际实验中，由于我们无法确认病毒所产生的速率是多少，还需要考虑和病毒有一定关系的其他因素，增强模型的可行性。因此，在原模型(1)上考虑一个感染单元的逃逸阶段，这个阶段中的单元可能还原为未感染的类。

本文引入HIV感染CD4⁺ T细胞模型：

$\{\begin{array}{l}{D}_{\ast }^{\kappa }x=\lambda -\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}-\mu x\left(t\right)+\delta w\left(t\right),\\ D_{\ast }^{\kappa }y=\varphi w\left(t\right)-\alpha y\left(t\right),\\ D_{\ast }^{\kappa }w=\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}-\left(\delta +\eta +\varphi \right)w\left(t\right),\\ D_{\ast }^{\kappa }v=\sigma y\left(t\right)-\gamma v\left(t\right),\end{array}$ (2)

$x\left(0\right)=x_0>0$， $y\left(0\right)=y_0>0$， $w\left(0\right)=w_0>0$， $v\left(0\right)=v_0>0$，其中 $0<\kappa \le 1$ 表示方程的阶数，变量 $x\left(t\right)$、 $y\left(t\right)$、 $w\left(t\right)$ 和 $v\left(t\right)$ 分别表示是未感染CD4⁺ T细胞、生产性感染细胞、逃逸阶段感染细胞和游离病毒的浓度。并且为了解释这些参数，我们记 $\lambda$ 为未感染CD4⁺ T细胞的补充率， $\mu$ 表示CD4⁺ T细胞的自然死亡率。而 $\beta x\left(t\right)v\left(t\right)/1+\alpha v\left(t\right)$ 表示健康CD4⁺ T细胞感染HIV的发生率，其中 $\beta$ 是感染率。参数 $\varphi$ 表示在逃逸阶段受感染细胞变成有生产力的受感染细胞的速率，这些细胞以速度 $\eta$ 死亡， $D_{\ast }^{\kappa }$ 表示Caputo型 $\gamma$ 阶的分数阶导数。

2. 模型有界性、基本再生数和平衡点存在性

2.1. 分数阶导数的定义

$J_0^{\kappa }f\left(x\right)=\frac{1}{\Gamma \left(\kappa \right)}{\displaystyle \underset{0}{\overset{x}{\int }}{\left(x-t\right)}^{\kappa -1}f\left(t\right)\text{d}t}$ (3)

函数 $f\left(x\right)$ 的 $\kappa$ 阶Riemann-Liouville分数阶导数定义为：

$D_0^{\kappa }f\left(x\right)={\left(\frac{\text{d}}{\text{d}x}\right)}^n{J}_0^{n-\kappa }f\left(x\right)=\frac{1}{\Gamma \left(n-\kappa \right)}{\left(\frac{\text{d}}{\text{d}x}\right)}^n{\displaystyle \underset{0}{\overset{x}{\int }}{\left(x-t\right)}^{n-\kappa -1}f\left(t\right)\text{d}t}$ (4)

其中 $n=\left[\kappa \right]+1$

函数 $f\left(x\right)$ 的 $\kappa$ 阶Caputo分数阶导数定义为：

$D_{\ast 0}^{\kappa }f\left(x\right)=J_0^{\kappa }{\left(\frac{\text{d}}{\text{d}x}\right)}^{n}f\left(x\right)=\frac{1}{\Gamma \left(n-\kappa \right)}{\left(\frac{\text{d}}{\text{d}x}\right)}^n{\displaystyle \underset{0}{\overset{x}{\int }}{\left(x-t\right)}^{n-\kappa -1}f\left(t\right)\text{d}t}$ (5)

其中 $n=\left[\kappa \right]+1$

由于 $f\left(t\right),f^{\left(1\right)}\left(t\right),f^{\left(2\right)}\left(t\right),\cdots$ 更贴合实际，所以接下来采用定理2.3。

定理2.2 设 $C^{\ast }\left[0,T\right]$ 是列向量 $x\left(t\right)$ 的连续空间，其中 $x\left(t\right)$ 的分量 $x_1,x_2,x_3\in C\left[0,T\right]$，则任意的 $x\left(t\right)\in C^{\ast }\left[0,T\right]$，其范数定义 [5] 如下：

$\Vert x\Vert ={\displaystyle \underset{i=1}{\overset{4}{\sum }}\underset{t}{\sup }}\left|x_i\left(t\right)\right|$

定理2.3 设矩阵 $A={\left(a_{ij}\right)}_{4\times 4}$，列向量 $\eta ={\left(a_{ij}\right)}_{4\times 1}$

$A=\underset{i}{\max }{\displaystyle \underset{i=1}{\overset{4}{\sum }}\left|a_{ij}\right|},\Vert \eta \Vert =\max \left|a_{ij}\right|$。

2.2. 模型的有界性

证明 首先，证明非负轨道 $R_{+}^4$ 是正不变的。由模型(2)有

$\{\begin{array}{l}{D_{\ast }^{\gamma }x|}_{x=0}=\lambda +\delta w\left(t\right)\ge 0,\\ {D_{\ast }^{\gamma }y|}_{y=0}=\varphi w\left(t\right)\ge 0,\\ {D_{\ast }^{\gamma }w|}_{w=0}=\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}\ge 0,\\ {D_{\ast }^{\gamma }v|}_{v=0}=\sigma y\left(t\right)\ge 0,\end{array}$

由推论 $f\left(x\right)\in C\left[a,b\right]$ 且 $D_a^{\kappa }f\left(x\right)\in C\left[a,b\right]$， $0<\kappa \le 1$。

若 ${D_a^{\kappa }f\left(x\right)|}_{x=a}\ge 0$， $\forall x\in \left(a,b\right)$，则对 $\forall x\in \left(a,b\right]$， $f\left(x\right)\ge f\left(a\right)$ ；

若 ${D_a^{\kappa }f\left(x\right)|}_{x=a}\le 0$， $\forall x\in \left(a,b\right)$，则对 $\forall x\in \left(a,b\right]$， $f\left(x\right)\le f\left(a\right)$。

可知模型(2)的解在 $R_{+}^4$ 中，进一步有：

$D_{\ast }^{\kappa }{x}_{tot}=\lambda -\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}-\mu x\left(t\right)+\delta w(\; t\; )$

其中 $x_{tot}=x+y$，由感染的CD4⁺ T细胞发生的死亡快于自然死亡，有 $\alpha >d$ 有：

$D_{\ast }^{\kappa }{x}_{tot}<\lambda -\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}-\mu x(\; t\; )$

这就完成了证明。

2.3. 模型平衡点的存在性

定义系统(1)的可行域(3)。应用类似文献 [6] 的方法，计算模型的基本再生数为

$R_0=\frac{\beta \lambda \sigma \varphi }{\left(\delta +\eta +\varphi \right)\alpha \gamma \mu }$，

经过计算，模型(2)有如下平衡点。

定理2.3 对于系统(2)，考虑其中复杂的生物过程的情况易得到以下平衡点：

为了得到模型(2)的平衡点，根据文献 [7] 计算平衡点的方法，令

$\{\begin{array}{l}{D_{\ast }^{\gamma }x|}_{x=0}=\lambda +\delta w\left(t\right)=0,\\ {D_{\ast }^{\gamma }y|}_{y=0}=\varphi w\left(t\right)=0,\\ {D_{\ast }^{\gamma }w|}_{w=0}=\frac{\beta x\left(t\right)v\left(t\right)}{1+\alpha v\left(t\right)}=0,\\ {D_{\ast }^{\gamma }v|}_{v=0}=\sigma y\left(t\right)=0,\end{array}$

解方程组(3)，易得模型(2)的平衡点。若 $\alpha =0$，则有平衡点

$E_0\left(0,0,0,0\right),E_1=\left(\frac{\lambda }{\mu },0,0,0\right),E_2=\left(0,\frac{\beta }{\alpha },0,1\right),E_3=\left(\frac{\lambda }{\mu },0,1,0\right),$

若 $\alpha \ne 0$，则有平衡点 $E^{\ast }=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$。

(1) 如果 $R_0<1$，则存在未感染平衡点

$E\left(0,0,0,0\right),E_0=\left(\frac{\lambda }{\mu },0,0,0\right),E_2=\left(0,\frac{\beta }{\alpha },0,1\right),E_3=\left(\frac{\lambda }{\mu },0,1,0\right),$

(2) 如果 $R_0>1$，则存在感染免疫平衡点 $E^{\ast }=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$，

其中

$x^{\ast }=\frac{\lambda }{\mu R_0},y^{\ast }=\frac{\varphi }{\partial }{w}^{\ast },w^{\ast }=\frac{\lambda }{\eta +\varphi }\left(1-\frac{1}{R_0}\right),v^{\ast }=\frac{\sigma \varphi }{\partial \gamma }{w}^{\ast }.$

证明 (1) $\frac{\text{d}v}{\text{d}t}=0$，即可得证。

(2) $\frac{\text{d}v}{\text{d}t}\ne 0$ 时，平衡点 $E_1=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$ 可由方程(3)所确定。

由上面方程的第四个式子得到

$v^{\ast }=\frac{\sigma \varphi }{\partial \gamma }{w}^{\ast },$

将 $v^{\ast }$ 的值代入上式子化简可得到

$x^{\ast }=\frac{\lambda }{\mu R_0},y^{\ast }=\frac{\varphi }{\partial }{w}^{\ast },w^{\ast }=\frac{\lambda }{\eta +\varphi }\left(1-\frac{1}{R_0}\right),$

所以 $R_0>1$，则存在感染免疫平衡点 $E^{\ast }=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$。

3. 平衡点的稳定性分析

3.1. 无病毒平衡的全局稳定性

作为推论，该区域将吸引方程(2)开始的所有解，并且它在方向上也是正不变的系统。我们通过观察模型(2)，方程的解 $E^{\ast }=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$ 称为模型的平衡点。

通常，在宿主种群中持续存在感染的一个充分条件是 $R_0>1$，这个条件对于大量的传染病模型(没有出现向后分叉现象的模型 [8]，对于 $R_0$ 低于单位数的模型也可能存在传染病传播)也是必要的。因此 $R_0=1$ 通常是介于流行病和疾病根除之间的一个阈值。正如我们将要展示的，这是模型(2)的情况。观察如果 $R_0>1$，那么存在一个唯一的感染均衡，即一个含有正成分的均衡： $E^{\ast }=\left(x^{\ast },y^{\ast },w^{\ast },v^{\ast }\right)$，且

$x^{\ast }=\frac{\lambda }{\mu R_0},y^{\ast }=\frac{\varphi }{\partial }{w}^{\ast },w^{\ast }=\frac{\lambda }{\eta +\varphi }\left(1-\frac{1}{R_0}\right),v^{\ast }=\frac{\sigma \varphi }{\partial \gamma }{w}^{\ast },$

在这一节中，我们证明如果 $R_0\le 1$，那么无病毒平衡是全局稳定的。因此，都在 $R_{+}^4$ 范围内求平衡点 $E^0$。

定理3.1 如果 $R_0\le 1$，那么无病毒平衡 $E^0$ 在 $R_{+}^4$ 中是全局渐近稳定的。

证明 定义全局李雅普诺夫函数

$L\left(t\right)=\left(x-x^0-x^0\ln \frac{x}{x^0}\right)+\frac{\delta }{2\left(\mu +\eta +\varphi \right)x^0}{\left[\left(x-x^0\right)+w\right]}^2+\frac{\left(\delta +\eta +\varphi \right)}{\varphi }y+w+\frac{\partial \left(\delta +\eta +\varphi \right)}{\sigma \varphi }v$

且W是 $R_{+}^4$ 内部的 $C^1$， $E^0$ 是 $R_{+}^4$ 上W的全局最小值， $W\left(x^0,0,0,0\right)=0$，其中 $x^0=\lambda /\mu$。

很明显，如果 $R_0\le 1$，对所有 $x,y,w,v>0$ 都有 $\text{d}W/\text{d}t\le 0$。因此，无病毒平衡 $E^0$ 是稳定的 [9]。更进一步， $\text{d}W/\text{d}t=0$，当 $x=x^0$ 和 $w=v=0$。设M是集合中最大的不变集

$E=\left\{\left(x,y,w,v\right)\in R^4:\text{d}W\left(x,y,w,v\right)/\text{d}t=0\right\}=\left\{\left(x,y,w,v\right)\in R^4:x=x^0,y\ge 0,w=0,v=0\right\}$

从(1)的第四个方程得出 $M=\left\{E^0\right\}$，根据LaSalle的不变性原理 [10]，无病毒平衡 $E^0$ 是全局渐近稳定的。

3.2. 感染平衡点的全局稳定性

接下来讨论感染病平衡点 $E^{\ast }$ 的全局渐近稳定性。首先构造函数，证明 $E^{\ast }$ 全局渐近稳定定理3.2。

定理3.2 $R_0>1$，如果

$1<R_0\le 1+\frac{\eta +\varphi }{\delta },$

那么唯一的感染平衡 $E^{\ast }$ 在 $R_{+}^4$ 内部是全局渐近稳定的。

证明 定义全局李雅普诺夫函数 [11]： $L:\left\{\left(x,y,w,v\right)\in R^4:x,y,w,v>0\right\}\to R$。这样：

$\begin{array}{c}L\left(x,y,w,v\right)=\left(x-x^{\ast }-x^{\ast }\ln \frac{x}{x^{\ast }}\right)+\frac{\beta x^{\ast }{v}^{\ast }}{\left(1+\alpha v^{\ast }\right)\varphi w^{\ast }}\left(y-y^{\ast }-y^{\ast }\ln \frac{y}{y^{\ast }}\right)\\ +\frac{\delta }{2\left(\mu +\eta +\varphi \right)}{\left[\left(x-x^{\ast }\right)+\left(w-w^{\ast }\right)\right]}^2+\left(w-w^{\ast }-w^{\ast }\ln \frac{w}{w^{\ast }}\right)\\ +\frac{\beta x^{\ast }{v}^{\ast }}{\left(1+\alpha v^{\ast }\right)\sigma y^{\ast }}\left(v-v^{\ast }-v^{\ast }\ln \frac{v}{v^{\ast }}\right)\end{array}$

如果 $\mu x^{\ast }-\delta w^{\ast }\ge 0$ 那么所有 $x,y,w,v>0$ 都是 $\text{d}L/\text{d}t\le 0$。因此，受感染的平衡点 $E^{\ast }$ 是稳定的，有 $\text{d}L/\text{d}t=0$，只有 $x=x^{\ast },y=y^{\ast },w=w^{\ast },v=v^{\ast }$ 成立，其中最大的不变集 $\left\{\left(x,y,w,v\right)\in R^4:\text{d}L/\text{d}t=0\right\}$ 是单独的 $\left\{E^{\ast }\right\}$。因此，受感染的平衡点 $E^{\ast }$ 是全局渐近稳定的，当 $R_0>1$ 时，LaSalle不变性原理 [12] 内部得到了验证。

4. 数值模拟4.1纸型、页边距与版式

在这一部分，用MATLAB数值模拟来验证系统(2)平衡点处的渐近稳定性。因此，令参数 $\varphi =\text{0}\text{.5}{\text{d}}^{-1}$， $\eta =0.7{\text{d}}^{-1}$， $\gamma =18{\text{d}}^{-1}$，初始条件设 $\lambda ={10}^4{\text{ml}}^{-1}\cdot {\text{d}}^{-1}$ ； $1/\mu =100\text{d}$ ； $\beta =1.5\times {10}^{-8}\text{ml}\cdot {\text{d}}^{-1}$ ； $1/\alpha =1\text{d}$ ； $\sigma =2000{\text{d}}^{-1}$，则基本再生数 $R_0=0.0628<1$ 取初值 $x\left(0\right)={10}^6{\text{ml}}^{-1}$， $y\left(0\right)=0$， $w\left(0\right)=0$，。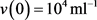用MATLAE软件进行数值模拟，得到系统的解的渐近状态，表明无病平衡点是全局渐近稳定的，如图1。

同理，带入不同的初值，得到系统的解的渐近状态，表明地方平衡点是全局渐近稳定的。如图2。数值模拟如下：

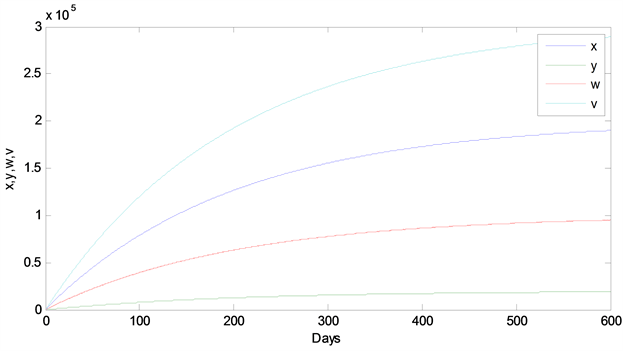
Figure 1. Global asymptotic stability of (2) disease-free equilibrium

图1. 系统(2)无病平衡点的全局渐近稳定性

Figure 2. Global asymptotic stability of the endemic equilibrium of the system (2)

图2. 系统(2)地方病平衡点的全局渐近稳定性

5. 结束语

本文得到了两个主要结果。首先，建立了带有HIV感染CD4⁺ T细胞的分数阶微分方程，证明模型存在正解。其次，证明了无病毒和感染平衡点全局渐近稳定的充分条件。感染平衡点的全局稳定性给出了以系统参数表示的条件，在此条件下病毒不能被消灭。通过李雅普诺夫函数，可以证明病毒自由平衡在基本再生数大于1时是全局渐近稳定的，并且在不等式存在的情况下，病毒自由平衡是全局渐近稳定的，我们确信确保被感染平衡的全局稳定性的参数值的范围比我们的条件所表明的要大。事实上，进行了一些数值模拟，表明被感染者当HIV感染模型存在时，它的平衡点是全局渐近稳定的。

项目编号

项目编号是X2018053。

参考文献