1. 引言
多项式因式分解是多项式基本运算的主要研究问题之一,也是Maple,Mathematica等计算机代数系统的主要功能之一。国内外很多学者对多项式因式分解问题进行了大量的研究。Lenstra和Lovasz [1] 首先提出了关于一元多项式因式分解的时间算法。该算法使用Berlekamp算法并结合Hensel引理对有限域上的多项式进行因式分解。Kaltofen和Von zur Gathen [2] [3] 给出了多元多项式因式分解的时间算法,并对该算法的时间复杂性进行了严格的证明。目前,精确的二元多项式因式分解时间复杂性最低的算法是由Lecerf [4] 提出的。Gao [5] 在Ruppert [6] 针对多项式微分形式相关结论的启发下,提出了一种新的因式分解算法。该算法首先利用Hilbert不可约定理,将多项式由多元降为二元,并提出了二元多项式任意域上的因式分解方法。
众所周知,多项式其系数微小的摄动都有可能改变其因式分解的结构。因此,对于系数有扰动的多项式,其因式分解计算是不连续的。于是当一个多项式系数的精确度有限时,其因式分解计算就显得十分困难。随着对多项式因式分解研究的逐步深入,学者们将研究工作从符号计算扩展到数值计算。Sasaki [7] 通过矩阵运算尽可能多的得到零和关系,提出了一种有效算法改进了多项式的近似因式分解算法。Gao、Kaltofen、May、Yang和Zhi [8] [9] 基于Ruppert和Gao针对多元多项式微分形式的研究成果,利用奇异值分解,结构总体最小二乘以及高斯–牛顿算法来计算多元多项式近似因式分解。Corless、Galligo和Giesbrecht等人 [10] [11] [12] 从几何角度研究了多项式因式分解问题。他们基于参数空间中的投影和随机环上的延拓法,从一个具有扰动的多项式中重建一个近似多项式及其不可约因子,通过建立因式分解的分层复解析流形及其管状邻域,设计了多项式因式分解的数值算法。Kahan [13] 发现了对于不适定代数问题不连续解的流形上隐藏的连续性,解决了对数据微小变化敏感的多项式因式分解的计算问题。Wu和Zeng [14] 提出了基于多项式空间几何和因式分解流形分层的数值分解概念,证明了多项式数值因式分解的存在性、唯一性、李普希茨连续性和收敛性,并提出了多项式数值因式分解算法。该算法消除了传统因式分解的病态性,将数值计算中的不适定因式分解问题完全正则化。
本文利用区间算法,在文献 [14] 工作的基础上设计了在确定因式分解流形结构下,与给定多项式残差向量2-范数最小的多项式的可信计算方法。
2. 预备部分
本文分别用
、
和
表示非负整数集合、实数集合和正实数集合。用
来表示
上的乘积顺序,对于
,
,
当且仅当
,
。用
表示
上的字典序,若向量
的最左边的非零项是正的,记为
。假设向量
的分
量为变量,
是一个
维矩阵,该矩阵的每一个分量都是关于变量
的函数,
表示分量为
的矩阵,其中
,
,
。
表示
维单位矩阵,
表示
维零矩阵。
令
是关于变量
的r元多项式环。令
为
中的单项,其中
。多项式
是单项式的有限线性组合,即f可以写成以下形式
令
表示多项式f关于变量
的次数,则多项式f的次数定义为
。令
表示
维向量,其分量是由多项式
f的系数按字典序降序排列而成的向量。文献 [8] [9] [15] 引入了多项式w关于次数
的卷积矩阵
,对于一个
的多项式w,矩阵
乘以
得到的向量为多项式w乘以多项式f所得的多项式其系数按照字典序排列而成的向量。
令
表示所有区间
构成的集合。区间向量
是一个分量为区间的n维向量组,且满足条件
区间矩阵
是具有区间项的矩阵,如果区间矩阵A中的任意实矩阵是满秩的,则称区间矩阵A满秩。如果属于区间矩阵
的任意实矩阵M,对所有的
,
满足条件
,则称区间矩阵M是区间对称矩阵。如果区间对称矩阵M中的每一个对称矩阵都为正定矩阵,则称区间对称矩阵M为区间对称正定矩阵。对于一个区间对称矩阵M,INTLAB工具箱 [16] 中的isspd函数可以验证M的正定性,即命令isspd (M)返回值为1,说明区间对称矩阵M为对称正定矩阵。
定理1 (见 [17]):设
,
,
是连续可微函数。对于
和区间向量
,其中
,令
表示
在区间
处的区间雅可比矩阵。给定
和满足条件
的区间矩阵
,若
则存在唯一的
,使得
,其中
表示
的内部。
3. 多项式近似因式分解
假设
是多项式
的近似因式分解,其中
,
,
,
是成对互质的无平方多项式,且对于任意的
,
。Wu和Zeng在文献 [14] 中提出了基于多项式空间几何和分解流形分层的数值多项式分解的概念,并且定义多项式全体近似因式分解的子集
(1)
Wu和Zeng称子集
中任意一个多项式的因式分解流形结构为
,并引入了以下向量
(2)
其中向量
的分量是按照关于
的字典序降序排列。然后,Wu和Zeng将求解因式分解流形结构
上的近似因式分解问题转换成计算下述超定方程组的最小二乘解
(3)
4. 主要结果
4.1. 数值部分
数值部分利用文献 [8] 中的数值多项式因式分解算法来计算因式分解流形结构
。然后,求超定方程组(3)的最小二乘解,得到该因式分解流形结构上高精度的近似解,记作
我们引入扰动向量
(4)
其中向量
的分量关于
的字典序降序排列。定义扰动多项式
为
为了简化表达式,令
,定义非线性函数
(5)
定义
非线性函数
的梯度为
(6)
其中
是多项式
关于次数
的卷积矩阵。关于变量
,有
对
的偏导数如下
(7)
注1:数值部分的主要工作是计算下列优化问题的稳定点
(8)
¨
通过引入拉格朗日算子
,定义拉格朗日函数
(9)
则有
(10)
由于
的Hession矩阵不包含变量
,
,为了方便起见将
写作
,显然,
(11)
注2:通过选择零向量作为初始值,数值部分采用数值牛顿迭代法
(12)
计算非线性系统
的近似解
。 ¨
4.2. 验证部分
验证部分分为两个阶段,第一阶段验证非线性系统
近似解的可信误差界,第二阶段验证优化问题(8)的稳定点是否为其局部最优解。
注 3:对于满足
的区间向量
,使用区间运算和式(6) (7) (11)计算区间雅克比矩阵
。利用定理1和verifynlss函数计算区间向量
和
,其满足条件存在实向量
和实向量
,使得
。 ¨
对每个
,令
表示
的维数,令
。记
,其中
。向量
,
和
的最后一项分别用
,
和 表示,令
表示,令 ,
, 和
和 分别表示向量
分别表示向量 ,
, 和
和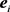 删除最后一项所得的向量。
删除最后一项所得的向量。
不失一般性,我们假设

对每一个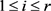 ,存在一个关于变量
,存在一个关于变量 的线性函数
的线性函数 ,其满足条件
,其满足条件
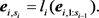
显然,

定义非线性函数

则有约束优化问题(8)可以转化为下面无约束优化问题
 (13)
(13)
验证部分第二阶段使用isspd函数验证区间Hession矩阵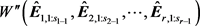 的正定性。当isspd函数返回值为1时,满足条件
的正定性。当isspd函数返回值为1时,满足条件 的实向量
的实向量 为问题(8)的局部最优解。
为问题(8)的局部最优解。
5. 主要算法
算法1
输入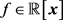
输出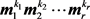 ,
,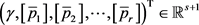 ,
,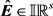 ,或“Failure”。
,或“Failure”。
步骤1 数值部分
步骤1.1 计算多项式f的因式分解流形结构 ;
;
步骤1.2 计算系统(3)的近似解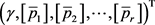 ;
;
步骤1.3 计算系统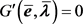 的近似解
的近似解 。
。
步骤2 验证部分
步骤2.1 初始化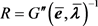 ,
, ,
, 和
和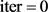 ;
;
步骤2.2 当 进行以下操作:
进行以下操作:
令 ;
;
 ;
;
计算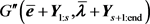 ;
;
令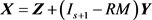 ;
;
若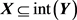 ,则令
,则令

如果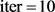 ,则返回“Failure”并停止。
,则返回“Failure”并停止。
步骤2.3 计算区间Hession阵 ,若isspd
,若isspd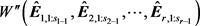 返回值为1,则输出
返回值为1,则输出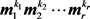 ,
, 和
和 ,否则,返回“Failure”。 ¨
,否则,返回“Failure”。 ¨
注4:在算法1中,给定实数x,则intval(x)输出区间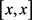 。给定实数a,b,其中
。给定实数a,b,其中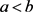 ,则
,则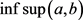 输出实区间
输出实区间 。给定
。给定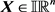 ,则
,则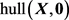 输出包含
输出包含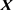 和零向量的最小的区间向量。 ¨
和零向量的最小的区间向量。 ¨
通过以上分析可以得到下述定理。
定理2:假设算法1成功输出因式分解流形结构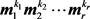 ,系数向量
,系数向量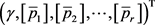 和摄动区间向量
和摄动区间向量 ,则存在一个实向量
,则存在一个实向量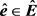 ,它是优化问题(8)的局部最优解。
,它是优化问题(8)的局部最优解。
6. 算例
例1 考虑多项式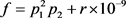 ,其中多项式
,其中多项式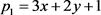 ,
, ,
,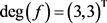 。摄动多项式r与f的次数相同且r的系数是[−5, 5]上随机的一个数。应用算法1可得
。摄动多项式r与f的次数相同且r的系数是[−5, 5]上随机的一个数。应用算法1可得

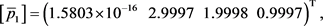
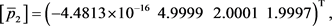

因此根据定理2,存在一个实向量 ,它是优化问题(8)的局部最优解。
,它是优化问题(8)的局部最优解。
例2 [14] 考虑多项式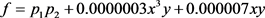 ,其中多项式
,其中多项式 ,
, ,
,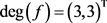 。应用算法1可得
。应用算法1可得



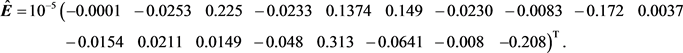
因此根据定理2,存在一个实向量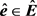 ,它是优化问题(8)的局部最优解。
,它是优化问题(8)的局部最优解。
例3考虑单变量多项式 ,其中多项式
,其中多项式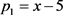 ,
, ,
, 。摄动多项式r与f的次数相同且r的系数是[−5, 5]上随机的一个数。应用算法1可得
。摄动多项式r与f的次数相同且r的系数是[−5, 5]上随机的一个数。应用算法1可得
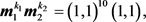


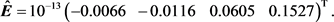
因此根据定理2,存在一个实向量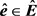 ,它是优化问题(8)的局部最优解。
,它是优化问题(8)的局部最优解。
基金项目
吉林省自然科学基金(批准号:11601039)。
NOTES
*通讯作者。