稀疏耦合神经网络的重构

Reconstruction of Sparse Coupled Neural Networks

摘要: 结合实际中神经网络的稀疏耦合特性，基于等式约束的L1优化方法下，本文发展了一类描述神经网络不规则放电动力学模型中耦合矩阵的重构方法，并通过数值模拟验证了该方法的有效性。与先前的基于SVD分解的重构方法相比较，本文的方法能在更短的观测时间内达到更高的重构精度。

Abstract: Considering the sparse coupling characteristic of real neural network, a method based on the L1 optimization method with equality constraints is developed to reconstruct the coupling matrix of the dynamic model of neural networks with irregular firing rate. The effectiveness of proposed method is verified by numerical simulation. Compared with the previous reconstruction method based on SVD decomposition, the proposed method can achieve higher reconstruction accuracy in a shorter observation time.

1. 引言

基于观测数据的网络重构是一个具有挑战性的问题，它在物理学、生态学、流行病学、遗传调控、生物化学和生物动力学等许多学科中有着重要的应用 [1] [2]。特别是在神经科学领域，比如：通过多通道脑电图信号 [3] 重构各脑区之间的连接关系等，揭示各脑区间的协调工作机理是脑科学研究领域的重要课题之一。

网络重构方法主要有两类：一种是通过观察观测量间的统计相关性揭示网络各节点间的相互作用关系，如Luo等人利用Granger因果关系重构基因网络 [4]；Yang等人利用Granger因果关系重构复杂定向网络等 [5]。第二种是假设观测的量可由复杂动力系统描述，并试图基于此复杂动力系统描述重构网络各节点间的关系，如：Wang等人基于压缩感知理论从少量的数据中揭示了交互网络 [6]；Huang等人基于贝叶斯压缩感知重构网络等 [7]。

动力学模型是描述神经网络的重要模型，在计算神经学中有着重要应用 [8]。在动力学模型中，神经网络由一组耦合的标量的微分方程描述。一些研究表明，当神经元间耦合强度较大时，神经元将呈现不规则放电行为 [9]。在神经元处于不规则放电的情况下，基于描述神经网络的动力学模型，Pikovsky提出了一种重构神经网络的方法 [9]。该方法的是通过相应的观测数据构造矩阵A，使得网络的耦合系数x满足 $Ax=0$，这样网络的重构问题则可转化为矩阵A的SVD (Singular Value Decomposition)分解方法求解。一般当观测数据充足的情况下，上述方法能够较准确的重构网络。然而，实际中获得系统的观测数据总是有限的，并且获得系统的观测数据成本昂贵。因此，在尽可能少的观测数据下实现系统的重构有着重要的现实意义和应用价值。考虑到实际中神经元间的连接具有稀疏性，本文将在Pikovsky方法的基础上，结合神经网络的稀疏耦合特性，利用等式约束的L₁优化方法重构网络，进一步降低重构网络所需的数据量，提高重构精度。

2. 模型与方法

2.1. 模型介绍

本文考虑计算神经科学中描述神经元放电的一般模型，模型中n个神经元的放电率 $x_i\left(t\right)$ 由如下微分方程描述 [10]：

${\tau }_i\frac{\text{d}{x}_i}{\text{d}t}+x_i=F_i\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{ij}{x}_j}\right)$， $i=1,\cdots ,n$。 (1)

其中 ${\tau }_i$ 是节点i的神经元的松弛常数， $F_i$ 是节点i的增益函数，神经元之间的耦合由 $n\times n$ 的矩阵 $W={\left\{w_{ij}\right\}}_{n\times n}$

确定。当神经元间的耦合足够强时，神经网络(1)会表现出混沌状态。混沌状态确保了神经元的放电率 $x_i\left(t\right)$ 有足够的可变性，这使得能够从 $x_i\left(t\right)$ 的观测值重构网络耦合矩阵。如果系统不是混沌状态，将无法完成重构，如周期轨道，稳定状态等 [9]。

2.2. 重构方法

在上述模型(1)中，假设可以观测得到关于 $x_i\left(t\right),{\stackrel{\dot{}}{x}}_i\left(t\right)$ 所有的时间序列，则问题变成从观测到的时间序列重构耦合矩阵W。一般情况下，增益函数 $F_i$ 未知且不同，本文的方法不需要知道 $F_i$ 的具体形式，只要求增益函数 $F_i$ 是双射。为了更加方便的讨论问题，本文主要讨论函数 $F_{\text{1}}$ 、常数 ${\tau }_{\text{1}}$ 以及耦合系数 $w_{1j}$，其他节点可类似的进行计算。

令 $c_j=w_{1j}\left(j=1,\cdots ,n\right)$，则向量 $c$ 表示耦合矩阵的第一行，即第一个神经元和其它神经元的耦合关系。假设参数 ${\tau }_{\text{1}}$ 已知，对一个给定的y值，找到 ${\tau }_{\text{1}}{\stackrel{\dot{}}{x}}_1+x_1$ 位于y的小邻域内的所有时刻，假设找到相对应的时

刻为 $t_{\text{1}},t_{\text{2}},\cdots ,t_{m+1}$。令 $x\left(t_k\right)=\left[x_1\left(t_k\right),x_2\left(t_k\right),\cdots ,x_n\left(t_k\right)\right]$，则对任意 $i,j\in \left[1,m+1\right]$， $F_1\left(c\cdot x\left(t_i\right)\right)\approx y$，

$F_1\left(c\cdot x\left(t_j\right)\right)\approx y$ 同时成立。由于本文采用的增益函数 $F_1$ 为双射，所以近似的有

$c\cdot x\left(t_i\right)\approx c\cdot x\left(t_j\right)$，

即

$c\cdot \left[x\left(t_i\right)-x\left(t_j\right)\right]\approx 0$。 (2)

又由 $c\cdot \left[x\left(t_i\right)-x\left(t_k\right)\right]\approx 0$， $c\cdot \left[x\left(t_i\right)-x\left(t_j\right)\right]\approx 0$ 可以推出 $c\cdot \left[x\left(t_k\right)-x\left(t_j\right)\right]\approx 0$，所以向量 $\left[x\left(t_i\right)-x\left(t_k\right)\right]$， $\left[x\left(t_i\right)-x\left(t_j\right)\right]$， $\left[x\left(t_k\right)-x\left(t_j\right)\right]$ 之间有较强的相关性。为了降低向量之间的相关系，我们进行如下计算形式的计算

$z\left(k\right)=\left[x\left(t_{k+1}\right)-x\left(t_k\right)\right]$， $k=1,\cdots ,m$。(3)

则方程(2)可写为

$z\left(k\right)\cdot c=\text{0}$。 (4)

由于(4)式的构造不依赖y，所以可以选取不同的y值找到一系列满足(4)式的 $z\left(k\right)$，把找到所有 $z\left(k\right)$ 组成矩阵A，则可得如下方程

$A\cdot c=0$。 (5)

于是重构神经网络的第一个节点的耦合系数转化为求方程(5)的非零解。一般情况下通过SVD对矩阵A进行分解，找矩阵A的最小奇异值 $\lambda$，则酉矩阵中最小奇异值 $\lambda$ 所的对应列为方程(5)的非零解。当观测数据充足的情况下，上述方法能够较准确的重构网络。然而，实际中获得系统的观测数据总是有限的，并且获得系统的观测数据成本昂贵，因此在尽可能少的数据条件下重构网络的连接有着重要的实际意义和应用价值。考虑到实际的神经网络常有稀疏耦合，所以对方程(5)增加稀疏限制条件，则变成

$\begin{array}{l}\text{min}{\Vert c\Vert }_{\text{1}}\\ \text{s}\text{.t}\text{.}0=A\cdot c\end{array}$。 (6)

其中 ${\Vert c\Vert }_{\text{1}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|c_i\right|}$ 是向量 $c$ 的L₁范数。显然零向量是优化问题(6)的最优解，但我们要寻找优化问题(6)的非零最优解。令 $c_i^{~}=c_i/{\displaystyle \underset{i=\text{1}}{\overset{n}{\sum }}{c}_i}$，则求解优化问题(6)的非零最优解问题转化为

$\begin{array}{l}\text{min}{\Vert c^{\text{~}}\Vert }_{\text{1}}\\ \text{s}\text{.t}\text{.}d=\bar{A}\cdot c^{\text{~}}\end{array}$。 (7)

其中矩阵 $\bar{A}=\left[\begin{array}{l}A\\ a\end{array}\right]$，向量 $a=\left[1,\cdots ,1\right]$，向量 $d={\left[0,0,\cdots ,0,1\right]}^{\text{T}}$。上述问题中等式约束的L₁优化问题，可在线性优化框架下求解 [11] [12]。

上述讨论是在 ${\tau }_{\text{1}}$ 已知的情况下进行，但现实生活中 ${\tau }_{\text{1}}$ 常是未知的。在这种情况下，我们可以给定 ${\tau }_{\text{1}}$ 一个合理范围，在不同的 ${\tau }_{\text{1}}$ 值下求解式优化问题(7)，其解记为 $\stackrel{⌢}{b}$。显然，正确的 ${\tau }_{\text{1}}$ 值应该使 ${\Vert \bar{A}\hat{b}-d\Vert }_{\text{2}}$ 取得最小值。

2.3. 数据处理

上一小节中，矩阵 $\bar{A}$ 的构造是在增益函数 $F_1$ 取相近的值时所对应的自变量取值也相近的假设下进行的。然而，由于神经网络模型中常用sigmoid函数作为增益函数。对于sigmoid函数存在着 ${\tau }_{\text{1}}{\stackrel{\dot{}}{x}}_1+x_1$ 导数接近于0的点，在这些点导致增益函数 $F_1$ 的反函数是近乎奇异的。因此，本文采用 $\left|\stackrel{\dot{}}{y}\right|>\delta$ 的条件除去导数接近于0，其中 $\delta$ 为选定的阈值。

一般情况下，通过观测数据构造矩阵 $\bar{A}$ 后，我们并不直接求解优化问题(7)，而是对矩阵 $\bar{A}$ 作进一步的处理。这里假设 $\bar{A}$ 为 $l\times n$ 维矩阵，对矩阵 $\bar{A}$ 做中心化和归一化处理，即

${a^{\prime }}_{ij}=\left({\bar{a}}_{ij}-{\displaystyle \underset{j=1}{\overset{l}{\sum }}{\bar{a}}_{ij}}/l\right)/{\Vert {\bar{a}}_{ij}-{\displaystyle \underset{j=1}{\overset{l}{\sum }}{\bar{a}}_{ij}}/l\Vert }_2$。(8)

对向量 $d$ 做中心化处理，即

${d^{\prime }}_j=d_j-{\displaystyle \underset{j=1}{\overset{l}{\sum }}{d}_j}/l$。 (9)

这样可以降低矩阵的每一列的振幅对优化求解的影响。进而，代替优化问题(7)，我们求解

$\begin{array}{l}\text{min}{\Vert c^{\prime }\Vert }_{\text{1}}\\ \text{s}\text{.t}\text{.}{d}^{\prime }=A^{\prime }\cdot c^{\prime }\end{array}$。 (10)

3. 数值模拟

本节将以随机网络和小世界网络为例对本文的重构方法进行模拟验证，并和SVD分解方法进行比较。

3.1. 随机网络

在数值模拟中，令节点数 $n=100$，松弛常数 ${\tau }_i\in \left[\text{0}\text{.9},1.1\right]$ 通过均匀分布产生。增益函为sigmoid函数： $F_i\left(u\right)={\alpha }_i/\left[1+\exp \left(-u-{\rho }_i\right)\right]$，其中 ${\alpha }_i\in \left[\text{0}\text{.9},1.1\right]$ 通过均匀分布产生； ${\rho }_i={\eta }_i-0.5\cdot {\displaystyle {\sum }_j{w}_{ij}}$，其中 ${\eta }_i$ 通过标准正态分布 $N\left(0,1\right)$ 产生。耦合系数矩阵W的元素以概率0.15生成，其取值通过正态分布 $\text{8}N\left(0,1\right)$ 产生。

图1展示了上述参数下生成的前10个 $x_i\left(t\right)$ 的混沌图像，此混沌状态是本文方法重构的前提。图2中的*表示根据 $\left|\stackrel{\dot{}}{y}\right|>\delta$ 的条件取得的数据，其中 $y={\tau }_{\text{1}}{\stackrel{\dot{}}{x}}_1+x_1$，采样时间间隔0.01，阈值常数 $\delta =\text{0}\text{.3}$。从图中清晰的看到随着时间t变化较快的y值保留下来，而几乎为恒定的y值被舍弃。

在图2获得的数据下，选取不同的 ${\tau }_1$ 值，利用本文的方法对网络进行重构，并计算相应的 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 的值。图3绘制了 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 的值随松弛常数 ${\tau }_1$ 的变化曲线，其中从下到上的曲线对应的观测时间分别为 $t=100,120,140,160$，竖直的直线表示正确的 ${\tau }_1$ 值。从图中看到 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 在正确 ${\tau }_1$ 附近取得最小值，因此可以通过寻找 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 最小值方法估计 ${\tau }_1$。在相同的数据下，利用SVD方法对网络进行重构，图4绘制了矩阵 $A^{\prime }$ 的最小奇异值 $\lambda$ 随 ${\tau }_1$ 的变化曲线，其中从下到上的图形对应的观测时间分别为 $t=100,120,140,160$，竖直的直线为正确的 ${\tau }_1$ 值。比较图3和图4，我们可以看出本文的方法在更短的观测时间给出 ${\tau }_1$ 值更为准确的估计。基于图3和图4确定的松弛常数 ${\tau }_1$，我们分别利用本文中等式约束的L₁优化方法和SVD方法对网络进行重构，图5展示了重构误差 ${\Vert w_1-{w^{\prime }}_1\Vert }_2$ 随观测时间t的变化曲线，其中 $w_1$ 代表正确的耦合系数， ${w^{\prime }}_1$ 为重构的耦合系数。通过图5，我们容易看出本文的方法在更短的观测时间内达到了更高精度的重构。

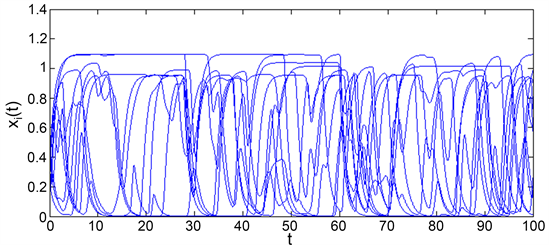
Figure 1. $x_i\left(t\right)\left(i=1,\cdots ,10\right)$ graph of changes over time

图1. $x_i\left(t\right)\left(i=1,\cdots ,10\right)$ 随时间的变化图

Figure 2. Data selected under the condition of $\left|\stackrel{\dot{}}{y}\right|>\delta$

图2. $\left|\stackrel{\dot{}}{y}\right|>\delta$ 的条件下选取的数据

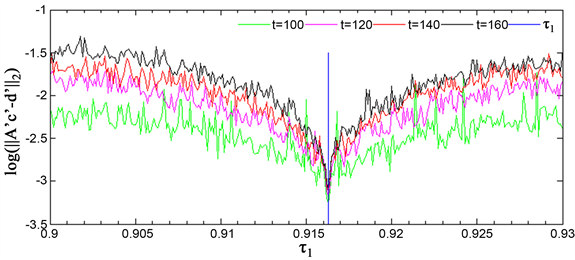
Figure 3. ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ versus ${\tau }_1$ change curve

图3. ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 随 ${\tau }_1$ 变化曲线

Figure 4. Curve of minimum singular value $\lambda$ versus ${\tau }_1$

图4. 最小奇异值 $\lambda$ 随 ${\tau }_1$ 变化曲线

Figure 5. Reconstruction error map of the two methods

图5. 两种方法的重构误差图

3.2. 小世界网络

小世界网络最早由Duncan Watts和Steven Strogatz在1998年引进的，将高聚合系数与低平均路径长度作为特征，提出的一种新的复杂网络结构。其构造算法为：首先给定一个具有n个节点的环形规则网络，每个网络节点 $V_i$ 左右对称地连接它的k个邻居节点，即左右每侧各有k/2个连接点，然后以概率 $P\left(0<P<1\right)$ 对其中任一个节点的每一条边进行断开重连，即保持该边一端不变，另一端重新选择一个新的节点连接，要避免自身连接和节点间的重复连接，以此节点开始，按顺序依次对每个节点进行边的重连，最后得到小世界网络 [13]。一些研究表明，生物学、物理学、社会学中大多数网络都具有小世界网络的特征，因此研究小世界网络具有广泛的现实意义。

本文中以节点数 $n=100$，每个节点的连接边数 $k=\text{10}$，连接概率 $P=\text{0}\text{.3}$ 产生小世界网络，网络中的其他参数设置与3.1中的随机网络相同，相应的数值模拟结果见图6~9。

图6展示了在随机网络的参数下生成的前10个 $x_i\left(t\right)$ 的小世界网络的混沌图像。

小世界网络的数据同样进行了图2方式的数据筛选。图7绘制了 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 的值随不同松弛常数 ${\tau }_1$ 的变化曲线，其中从下到上的曲线对应的观测时间分别为 $t=\text{170},190,210,230$，竖直的直线表示正确的 ${\tau }_1$ 值。从图中看到 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 在正确 ${\tau }_1$ 附近取得最小值，因此可以通过寻找 ${\Vert A^{\prime }{c}^{\prime }-d^{\prime }\Vert }_{\text{2}}$ 最小值方法估计 ${\tau }_1$。在相同的数据下，利用SVD方法对网络进行重构，图8绘制矩阵 $\hat{A}$ 的最小奇异值 $\lambda$ 随 ${\tau }_{\text{1}}$ 的变化曲线，其中从下到上的图形对应的观测时间分别为 $t=\text{170},190,210,230$，竖直的直线为正确的 ${\tau }_{\text{1}}$ 值。比较图7和图8，我们可以看出图8中在时间 $t=\text{170}$ 未能找到正确的 ${\tau }_{\text{1}}$ ；当时间 $t>170$，找到的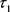存在误差，即在小世界网络中本文的方法在更短的观测时间给出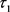值更为准确的估计。基于图7和图8确定的松弛常数，分别利用本文中等式约束的L₁优化方法和SVD方法对网络进行重构，图9展示了重构误差随观测时间t的变化曲线，其中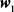代表正确的耦合系数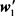，为重构的耦合系数。通过图9，我们容易看出在小世界网络中本文的方法在更短的观测时间内达到了更高精度的重构。

Figure 6. graph of changes over time

图6.随时间的变化图

Figure 7. versus change curve

图7.随变化图

Figure 8. Curve of minimum singular value versus

图8. 最小奇异值随变化图

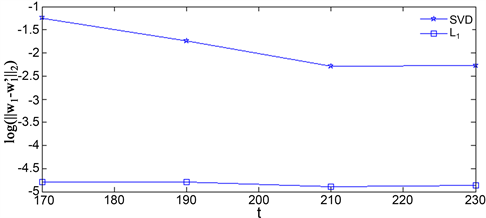
Figure 9. Reconstruction error map of the two methods

图9. 两种方法的重构误差图

4. 结束语

基于观测数据的网络重构是一个具有挑战性的问题，特别在神经科学领域，通过多通道脑电图信号重构各脑区之间的连接关系，揭示各脑区间的协调工作机理是脑科学研究领域的重要课题之一。本文在先前Pikovsky工作的基础上，结合实际中神经网络的稀疏耦合特性，基于等式约束的L₁优化方法，发展了重构一类描述神经网络不规则放电动力学模型中耦合矩阵的重构方法，并通过数值模拟验证了该方法的有效性。与Pikovsky的基于SVD分解的重构方法相比较，本文的方法能在更短的观测时间内达到更高的重构精度。由于实际的观测数据十分有限，因此发展在更少的数据量下重的网络重构方法是我们进一步的研究目标。此外，本文的方法和基于SVD分解的重构方法一般自适用于节点较少的小型网络系统，发展大型网络系统的重构方法是我们的另一研究目标。

基金项目

长安大学高新技术培育项目(300102129202)，长安大学卓越青年项目(310812163504)。

NOTES

^*第一作者。

^#通讯作者。