1. 引言
迭代函数系统是一个重要的研究对象并得到了广泛的研究。很多数学家对迭代函数系统进行了研究,如Mauldin [1] [2],Urbanski [1] [2],Inui [3] [4],Sumi [3] [4],Roy [5],Qiu [6] [7],Bandt [8],Hutchinson [9],Falconer [10],Moran [11],Fan [12] 和Schief [13] 等都研究了迭代函数系统极限集的维数和测度等性质。
在文献 [1] 中为了说明广义连分数的共形迭代系统极限集的Hausdorff 测度等于零,填充测度大于零,Maulain 和Urbanski构造了一个与连分数有关的共形迭代函数系统。记
为复数集,
表示整数集,
表示正整数集。他们所构造的方法是设
,则称
为连分数共形迭代系统。其中
在文献 [3] [4] 中Inui,Okada和Sumi研究了更一般的情况,他们的构造如下。设
,
.
给定任意
,设
,
被称为广义复连分数共形迭代函数系统(如图1所示),其中
在 [4] 中,作者证明了对上述广义复连分数共形迭代系统 [1] 中的结论依然成立,在 [3] 中,作者讨论了一个新的问题,Hausdorff维数关于参数
的连续依赖性,他们的主要结果是:
设
为
的极限集,
为极限集
的Hausdorff维数。
定理1.1 设
为广义复连分数共形迭代函数系统族,则
(1)
在
上是连续的。
(2) 对任意
,
是
压力函数的唯一零点。
(3)
,
。
特别地,
在
上不是常值映射。
定理1.2设
为广义复连分数共形迭代函数系统族,则
在
是实解析和次调和的。
推论1.3设
为广义复连分数共形迭代函数系统族,则函数
存在最大值,并且在
的边界取得
最大值的点。特别地,
。
在本文中我们进一步推广了 [3] 中结果, [4] 中结论是否成立我们将在下一篇文章中讨论。
设
;
;
,其中
,
,
令
,
,
,这里
。
定义1.4 (广义复连分数的共形迭代函数系统)对任意
,
被称为广义复连分数共形迭代函数系统。其中
称
为广义复连分数共形迭代函数系统族(如图2所示)。对每个
,设
为
的极限集,设
为极限集
的Hausdorff维数。用
表示在复平面
上的拓扑意义下H的内点。
本文将文献 [3] 中的结论推广到更一般的情形,即更大广义复连分数共形迭代系统
,我们的主要定理为:
定理1.5设
为广义复连分数共形迭代函数系统族,则
(1)
在H上是连续的。
(2) 对任意的
,
是
压力函数的唯一零点。
(3)
,
。
特别地,
在H上不是常值映射。
定理1.6设
为广义复连分数共形迭代函数系统族,则
在
是实解析和次调和的。
推论1.7设
为广义复连分数共形迭代函数系统族,则函数
存在最大值,并且在H的边界取得
最大值的点。特别地,
。
2. 共形迭代函数系统
此章节主要是介绍共形迭代函数系统的构造以及一些相关概念 [1] [2] [5]。
定义2.1 (共形迭代函数系统)设
是非空紧致连通集,I是有限集或者对等于
。假设I至少含有两个元素,当S满足以下几个条件时,我们称
是共形迭代函数系统。
1. 单射:对所有的
,
是单射。
2. 一致压缩性:
,使得对
,
下面不等式成立。
3. 共形性:存在一个正数
和开连通子集
并且
,使得对
,
可延拓为V上的
微分同胚,且
在V上是共形的。
4. 开集条件:对
,
,并且
。这里
表示在
拓扑空间下X的内点。
5. 有界偏差性:
使得对所有的
,对所有的
,下面不等式成立
6. 锥条件:对所有的
,存在一个开锥
,其中x为顶点,u为方向,
为高度,
为角度,使得
是
的子集。
设S是一个共形迭代函数系统。对任意的
,设
且
,则有
是一个单点,用
来表示该单点。定义S中的编码映射
为
,注意到
是连续的,进而S中的极限集可定义为
对每个迭代函数系统S,设
,
表示Hausdorff维数。对任意的S,定义S的压力函数如下。
定义2.2 (压力函数)
,值域在
上的函数
设
则称函数
为S的压力函数。
性质2.3对任意的
,且
有
。特别地,当
时,对于任意的
,
是次可加的。
根据性质2.3可得对任意的
,
都存在。设
。运用压力函数可以得到共形迭代函数系统的一些性质。
定义2.4 (正则,强正则,继承正则) 设S是一个共形迭代函数系统,
(1) 若存在
使得
,称S是正则的。
(2) 若存在
使得
,称S是强正则。
(3) 若对所有的
且有
时,
是正则的,则称S是继承正则。这里,对任意集合A,用
来表示A的基数。如果一个共形迭代函数系统S是继承正则的,则S也是强正则;如果S是强正则,则S也是正则的。设
,对每个
,设
。
定理2.5 ( [1] Theorem 3.15) 设S是一个共形迭代函数系统,则
另外,如果存在
使得
。则t为压力函数
的唯一零点,有
。
定理2.6 ( [1] Theorem 3.20) 设I是无限的,S是一个共形迭代函数系统,则下面两个条件等价:
1. S是继承正则的。
2.
。特别地,如果S是继承正则,有
。
定理2.7 ( [1] Proposition 4.4) 设S为正则共形迭代函数系统。若
,则
。这
里的
表示d维勒贝格测度且
。
接下来考虑共形迭代函数系统族。设
为所有共形迭代函数系统族,其中
,I为无限序列集。现要在
上赋予一种
-拓扑 [4]。对
,记
为
,S为
。设
为S的编码映射。在本文中,
中任意序列若满足下面条件,则称序列
依
照记
-拓扑收敛到S,记为
。
(D1)
,
。
(D2) 若存在
,
和一有限集
使得
和
,有
。
若
中的序列
不收敛于任何
,即当上面的条件不满足时称
。若
时,称序列
为
收敛。
定义2.8设
是
中的开连通子集。
是
中的一族,其中
为
。若
,
,
在
上全纯,则
称是平面解析的。若存在
使得下面的条件成立,则称平面解析的
为正则平面解析。
(1)
是强正则。
(2)
使得对所有的
,
,
。
其中,对每个
和
,
,
定理2.9 ( [5] Theorem 5.10) 当
被赋予了
上的拓扑时,Hausdorff维数函数
,
是连续的。
定理2.10 ( [5] Theorem 6.1) 设
是
中的开连通子集,
是
中的一族。若
是正则平面解析的,则
在
上是实解析的。
定理2.11 ( [5] Theorem 6.3) 设
是
中的开连通子集,
是
中的一族。若
是
平面解析的,则
在
上是上调和映射。
3. 广义复连分数的共形迭代函数系统
这个部分主要是证明广义复连分数的共形迭代函数系统的一些性质 [3] [4]。在不致混淆的情况下可简记下面的记号。设
,
,
和
,
表示复数的实部,
表示复数的虚部。
性质3.1
,
是一个共形迭代函数系统。
证明:设
,首先证明
,
。设
,并且设
为莫比
乌斯变换,定义为
。因为
,
,
,可知
,又因为
,所以
。因此
是同胚的。设
,
。
可推得
,并且
,因此证明了
。
接下来要证对每个
,
满足定义2.1中的条件。
1. 单射
因为每个
都是莫比乌斯变换,所以每个
是单射。
2. 一致压缩性
设
,
,则
。
(i) 设
是
中的元素,设
、
,有
可得
。同理可得
,则
因此
在X上一致压缩。由对称性可知
在X上一致压缩。
(ii) 设
是
中的元素,设
,
,有
可得
,同理可得
,则
因此
在X上一致压缩。综上,
在X上一致压缩。
3. 共形性
设
,
。因为
在
上是全纯的,
是
的并且在V上共形。
4. 开集条件
记
。设
,
,因为
,可以推得
,
设
,
为两个不同的元素时,
当
时,
当
时,因为
,
,
(1)
若
,因为
故(1)式大于1;当
,此时
由条件知
,
,
,
使得
,又
,知
,故当
为两个不同的
元素时,
和
不相交。则对所有的
,
故
满足开集条件。
5. 有界偏差性
取足够小的
,且
。设
是以
为中心,
为半径的开球,记
,
并设
,
,
有
(i) 当
时
(ii) 由对称性知当
时,同样有
。
(iii) 当
时
故
,有
。
对每个
,设
则有
,
可以推出
。因此
,并且
说明对所有的
,
。因为
是
上的单射,
在
上是全纯的,所以
在
上是全纯的。
设b是
中的一个元素,
,设
为
因为
在D上是全纯的,且
,
。用克贝偏差定理,可推知对所有的
,
设
,可推知存在
和
使得对任意的
,
设
,
即证对任意的
,
。
最后设
为
为中心,
为半径的开球,则V是
的开连通子集,且有
,
,
因此
满足有界偏差条件。
6. 锥条件
因为X是闭圆盘,所以满足锥条件。
引理3.2设
,则存在
使得对所有的
,
,有
.
证明:因为
,由有界偏差条件知存在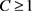 使得对任意的
使得对任意的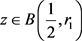 ,
,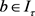 ,有
,有
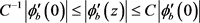 。因此有
。因此有 。
。
引理3.3对任意的 ,
,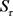 是继承正则的共形迭代函数系统,且有
是继承正则的共形迭代函数系统,且有 。
。
证明:设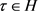 ,对任意的正整数
,对任意的正整数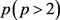 ,定义
,定义
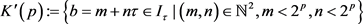 ,
,
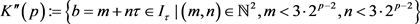 及
及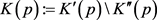 。
。
由几何性质知 ,
,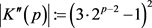 可以推出
可以推出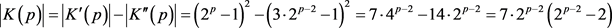 ,且有
,且有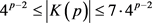 。
。
设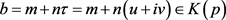 ,考虑下面两种情况
,考虑下面两种情况
(i) 若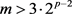
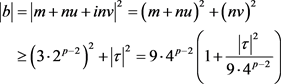
(ii) 若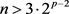
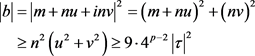
对任意的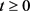 ,
,
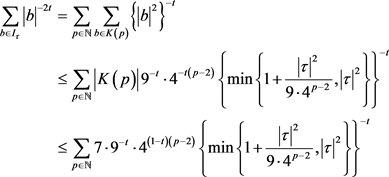
因此推出
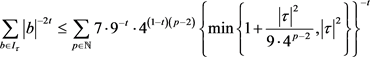 (2)
(2)
另外,由不等式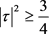 及不等式
及不等式 ,知对任意的
,知对任意的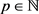 ,
,
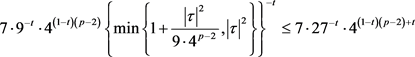 (3)
(3)
又由不等式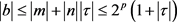 ,有
,有
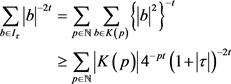
因此可以推知
 (4)
(4)
结合引理3.2及不等式 (2),(4)可知 ,若
,若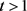 ,则
,则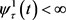 ,因此可知
,因此可知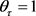 。并且由定理2.6可得对所有的
。并且由定理2.6可得对所有的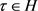 ,
, 是继承正则的。
是继承正则的。
引理3.4 。即对
。即对 ,
, ,使得对所有的
,使得对所有的 且
且 时,
时, 成立。
成立。
证明:设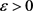 ,
,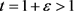 ,设H中的序列
,设H中的序列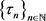 使得
使得 时,
时, 。注意到对任意的
。注意到对任意的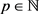 ,
,
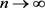 时,有
时,有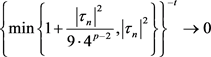 。通过不等式(2)和不等式(3)可推出
。通过不等式(2)和不等式(3)可推出

主要是由整函数控制的,即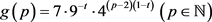 ,由勒贝格控制收敛定理可知
,由勒贝格控制收敛定理可知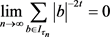 。
。
由引理3.2得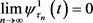 ,即
,即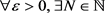 使得对任意的
使得对任意的 ,
,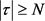 有
有 。
。
再由性质2.3知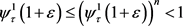 。根据定义可知
。根据定义可知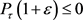 ,故对任意的
,故对任意的 ,存在
,存在 使得对所有的
使得对所有的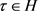 ,
,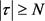 ,
, 。由定理2.6,对任意的
。由定理2.6,对任意的 ,有
,有 ,证毕。
,证毕。
定理3.5设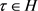 ,有
,有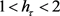 。
。
证明:由定理2.6知 ,接下来只需证
,接下来只需证 。
。
(i)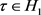 时
时
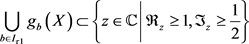
设 为一开球,且
为一开球,且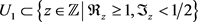 ,因为
,因为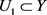 ,可以推得
,可以推得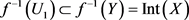 。
。
设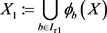 ,因为
,因为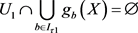 ,所以
,所以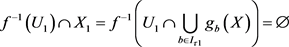 ,即有
,即有 。
。
(ii)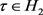 时,由对称性可知存在
时,由对称性可知存在 使得
使得 。
。
(iii)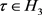 时
时

设 为一开球,且
为一开球,且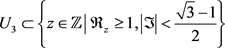 ,因为
,因为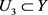 ,可以推得
,可以推得 。设
。设 ,因为
,因为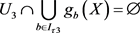 ,所以
,所以
 ,即有
,即有 。
。
综上,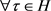 ,设
,设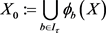 ,都能找到
,都能找到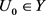 使得
使得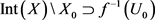 。因此
。因此
 ,这里
,这里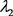 表示2维勒贝克测度。由定理2.7得
表示2维勒贝克测度。由定理2.7得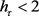 。
。
4. 主要结论的证明
4.1. 定理1.5的证明
为了证明定理1.5,要用到下面的引理,并在此给出证明。
引理4.1设 ,序列
,序列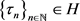 满足
满足 ,则存在
,则存在 ,
,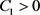 ,
,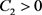 使得对所有的
使得对所有的
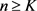 ,
, ,
,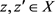 ,有
,有
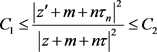
证明:设 ,对每个
,对每个 有
有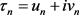 ,因为
,因为 ,则
,则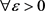 ,
,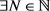 ,当
,当 时,
时, ,
,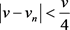 。对任意的
。对任意的 ,
,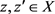 ,一方面,
,一方面,
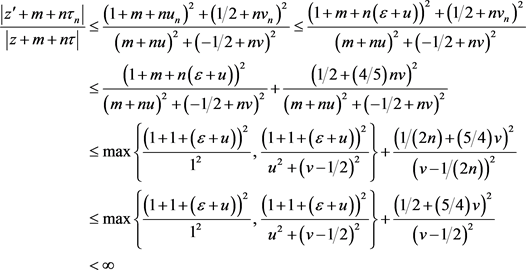
另一方面,
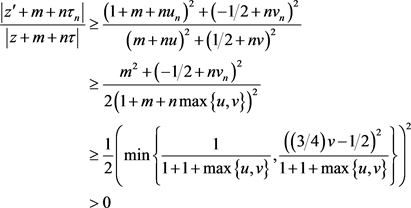
即存在 ,
,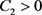 使得
使得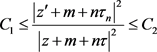 。
。
现在证明定理1.5。
证明:通过引理3.3知对H中的每个 ,
, 的值为
的值为 的压力函数的零点。由引理3.4,3.5知对任意
的压力函数的零点。由引理3.4,3.5知对任意
 ,有
,有 并且当
并且当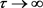 时,
时,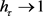 。接下来证若H中的序列
。接下来证若H中的序列 满足
满足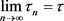 时,有
时,有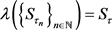 。
。
对任意的 ,
, ,
, ,满足条件(D1)。因为X是完
,满足条件(D1)。因为X是完
备的,因此存在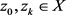 使得
使得
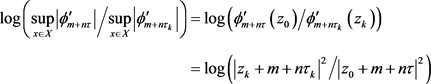
由引理4.1知存在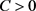 ,
,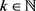 使得对每个
使得对每个 ,
,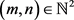 ,
,
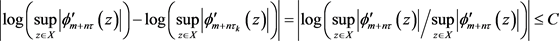
故证明了H中的序列 满足
满足 ,有
,有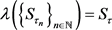 。
。
最后证明 在H上是连续的。根据定理2.9,在
在H上是连续的。根据定理2.9,在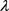 拓扑下
拓扑下 是连续的。由 [8] 中引理3.3,
是连续的。由 [8] 中引理3.3,
若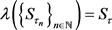 ,则
,则 。因此若
。因此若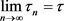 ,则
,则 ,故证明了
,故证明了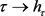 在H上是连续的。
在H上是连续的。
4.2. 定理1.6的证明
为证明定理1.6要用到下面两个定理。
引理4.2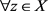 ,
,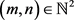 ,以及
,以及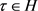 ,当
,当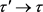 时有
时有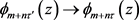 并且收敛唯一。
并且收敛唯一。
证明:设 ,
, ,
, 则有
则有

故引理得证。
引理4.3对任意的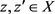 ,
, ,下式成立。
,下式成立。

证明:设 ,
,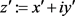 及
及 则
则
当 时
时

最后一个不等式是因为当设 时,
时,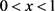 ,取
,取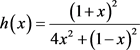 ,求导后知在
,求导后知在 时取得最大值。当
时取得最大值。当 时,由对称性有
时,由对称性有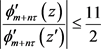 。故引理得证。
。故引理得证。
现在证明定理1.6.
证明:首先说明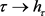 在
在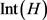 上是次调和的。
上是次调和的。
设 ,
,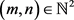 ,可以推知
,可以推知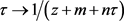 是全纯函数。因为
是全纯函数。因为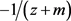 的实部是负的,即
的实部是负的,即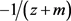 不是
不是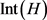 中的元素,因此
中的元素,因此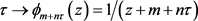 在H上是全纯的。故
在H上是全纯的。故 是平面解析的。再由定理2.11,可得
是平面解析的。再由定理2.11,可得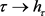 在
在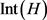 上是次调和的。
上是次调和的。
接下来说明上是平面解析的。对任意的 ,
,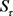 是继承正则共形迭代函数系统,故对任意的
是继承正则共形迭代函数系统,故对任意的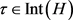 ,
,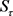 是强正则共形迭代函数系统。因此
是强正则共形迭代函数系统。因此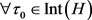 ,存在一个中心为
,存在一个中心为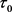 的开球
的开球 ,以及
,以及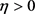 使得所有的
使得所有的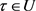 ,
, ,
, ,其中
,其中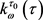 表示
表示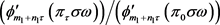 ,有
,有
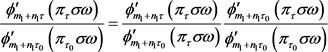
由引理4.2知当 趋向
趋向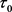 时,上式右边第一部分趋向1;由引理4.3知
时,上式右边第一部分趋向1;由引理4.3知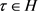 ,
, 条件下,上式右边第二部分是有界的。因此存在中心为
条件下,上式右边第二部分是有界的。因此存在中心为 的开球
的开球 使得
使得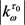 在
在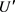 中有界。运用Cauchy公式
中有界。运用Cauchy公式
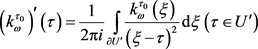
可推出存在一个 使得对任意的
使得对任意的 ,有
,有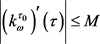 。这里
。这里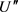 是中心在
是中心在 且
且 ,则
,则

说明存在一个中心在 的开球
的开球 使得对任意的
使得对任意的 ,
,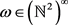 ,
, 。因此对
。因此对
任意的 ,存在一个中心在
,存在一个中心在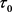 的开球
的开球 使得
使得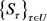 是正则平面解析的。由定理2.10知对任意的
是正则平面解析的。由定理2.10知对任意的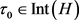 存在一个中心在
存在一个中心在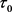 的开球
的开球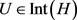 使得
使得 是实解析的。由
是实解析的。由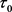 的任意性可知映射
的任意性可知映射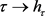 在
在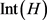 上是实解析且次调和的。
上是实解析且次调和的。
4.3. 推论1.7的证明
证明: ,设
,设 。由定理1.6,对任意的
。由定理1.6,对任意的 ,映射
,映射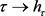 在
在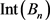 上是次调和的。设
上是次调和的。设 ,这里
,这里 。由引理3.4知存在
。由引理3.4知存在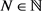 使得对所有的
使得对所有的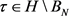 ,有
,有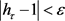 ,即
,即 。故对任意的
。故对任意的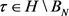 ,
,

因为 在
在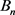 上是连续的,则在其上存在一个最大值
上是连续的,则在其上存在一个最大值
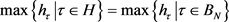
由 在
在 上次调和,故在其中没有最大值,取得最大值的点只能在边界上。综上推论1.7证毕。
上次调和,故在其中没有最大值,取得最大值的点只能在边界上。综上推论1.7证毕。