1. 引言
随着社会经济的快速发展,人类活动对河流的干扰日益增大,河流的各方面功能正逐渐丧失。这不仅关系到河流自身的健康,还会严重阻碍到人类社会的可持续发展 [1]。近年来,人们已经充分认识到保护河流健康的重要性,河流健康评价渐渐成为河流管理工作中最重要的一环。
根据评价对象的不同,河流健康评价的方法可分为两大类:指示物种生物监测法和涵盖多因素的综合评价方法 [2]。指示物种生物监测方法在20世纪80年代开始流行,它由河流无脊椎动物预测与分类系统(RIVPACS)和生物完整性指数法(IBI)两种方法组成。但是由于水生生物只是整个河流水生态系统的一部分,上述方法的评价并不全面。因此,综合考虑河流健康多方面因素的评价方法被提出。这类方法的关键是建立一个完善的评价体系,体系中尽可能多地包含影响河流健康的因素,常用的方法包括主观评价模型中的可变模糊集 [3]、神经网络 [4] 等,以及客观评价方法中的熵权模型 [5] [6]、模糊物元模型 [7] 等。
整个河流系统是一个比较复杂的体系,影响河流健康的因素涵盖了自然和人为两个方面,它们的规律各不相同并且难以量化,各自之间具有不相容性,这给河流健康评价带来了模糊性和不确定性 [8] [9]。由于模糊物元法能够较好地解决评价过程中所带来的随机和模糊等不确定性,并能将所有单个的指标转换为一个整体进行评价,相较于其他方法更为简便通用,因而它越来越多地被运用在河流健康评价当中 [10]。周振民等将熵值法与模糊物元法相结合,建立了地下水水质评价模型,模型简便、通用,计算结果较为客观和稳定 [11]。Zhao等将模糊评价方法与层次分析法相结合,建立了综合模糊层次评价模型,并对永河进行了健康评价,验证了模型的有效性 [2]。刘倩等基于可拓物元法的递阶层次架构和改进模糊优选理论中的隶属度建立了模糊物元河流健康评价模型,并将其应用于滦河河流健康评价中,模型评价结果与实际情况相符 [12]。
但是以往的研究存在以下三个局限性:①较少对受多闸坝调控的河流开展健康评价,②指标体系建立时水生态部分往往只关注了水生动物,③对河流的社会属性指标的评价考虑不足。基于此,本文从水文、水质、水生态和社会服务四个方面构建了一套新的河流健康综合评价指标体系,将模糊物元法与熵权法有机地结合,以淮河最大的支流沙颍河为例进行了河流健康评价,以期为流域的保护和管理提供决策依据。同时,本文通过设置两个情景,论证了考虑河流社会服务功能的必要性。
2. 研究方法
2.1. 评价体系
2.1.1. 评价体系指标
建立河流健康评价指标体系的基础是科学地通过选择适当指标,反映和衡量河流所处的状态,从而为寻求河流的可持续发展提供方向。考虑到评价指标的跨学科跨领域和种类、项目繁多的特点 [13],本文筛选了4类代表性的指标,分别反映河流的水文水资源、水质、水生态和社会服务方面,旨在尽可能涵盖河流完整的功能。
1) 水文水资源
为了维持河流生态系统的生态环境功能,河流必须要能够提供足够的水量。本文选取水文学中生态流量的指标,计算其满足程度来表征河流径流量满足其生态系统需求的程度。生态流量满足度是河流流量能够满足生态流量的天数与总天数的比值,计算公式如下:
(1)
(2)
式中,αij表示第i年第j月的生态流量满足度;Dij表示第i年第j月生态流量的满足天数(d);D表示第i年第j月的总天数(d);Qijk表示第i年第j月第k日的河道流量(m³/s);Qij表示第i年第j月的生态流量(m³/s)。
2) 水质
保障河流健康不仅需要提供足够的水量,也需要保证合格的水质。本文根据《地表水环境质量标准》(GB 3838-2002),选取了以下四个评价项目:DO水质状况、有机污染水质状况、无机污染水质状况和重金属污染状况。其中有机污染水质状况包含高锰酸盐指数、化学需氧量、五日生化需氧量、氨氮4个水质指标,无机污染水质状况主要考虑总磷指标,重金属污染状况包含铜、锌、硒、砷、汞、镉、六价铬、铅8个水质指标。
对于只包含一个指标的DO水质状况和无机污染水质状况,其项目值采用相应水质指标评估年的平均浓度。对于包含多个指标的有机污染水质状况和重金属污染状况,将它们各自包含的水质指标分别进行赋分,见表1和表2。根据监测数据,每个水质指标将其全年12个月的月均浓度按照汛期和非汛期分别进行平均,再分别确定汛期与非汛期的赋分,取其最低赋分作为此水质指标的赋分,最后取所包含的各个指标的赋分平均值作为该项目的赋分 [13]。

Table 1. The score distribution of organic pollution
表1. 有机污染水质状况水质指标赋分

Table 2. The score distribution of heavy metal pollution
表2. 重金属污染状况水质指标赋分
3) 水生态
水生态健康调查评价中,大多数指标体系只考虑了水生动物,而评价一条河流时,这样的考虑过于笼统和片面。因此本文将水生动物分为底栖动物和浮游动物,另外将浮游植物也考虑其中,采用Shannon Wiener指数来评价它们的多样性 [14],计算公式如下:
(3)
式中,S表示总种数;pi表示第i种类的个体数占总个体数的比例。
4) 社会服务
河流健康是自然价值与人类社会服务价值的统一体,健康不仅意味着自然功能的完整性,还要确保其社会功能的正常发挥 [12]。以往的研究往往只从水文、水质和水生态的角度去分析河流健康,忽略了水的“社会–自然”二元特性。人类活动对河流健康的影响越来越大,经济需水和生态需水的矛盾越来越突出 [15]。本文充分考虑河流完整的功能,在评价指标中加入体现社会服务功能的通航水位保证率和水资源开发利用率两个指标。
河道航运功能的保证能促进货物的顺利流通,有利于社会经济的发展。河道航运功能的保证采用通航水位保证率来衡量,计算公式如下:
(4)
(5)
式中,βij表示第i年第j月的通航水位保证率;Dij表示第i年第j月通航水位得到满足的天数(d);D表示第i年第j月的总天数(d);Zijk表示第i年第j月第k日的河道水位(m);Zij表示第i年第j月的通航水位(m)。
水资源的开发利用是改造和利用自然的一个方面,其目的是发展社会经济,产生社会效益。水资源开发利用的内容很广,包括农业灌溉、工业用水和生活用水等等。本文用水资源开发利用率来衡量水资源开发利用程度,计算公式如下:
(6)
式中,Ru为水资源开发利用率;Wu为已开发利用的水资源总量;Wt为流域的水资源总量。
2.1.2. 评价体系建立
结合上述河流四个方面的特性,选取的河流健康综合评价体系见表3。

Table 3. River health comprehensive evaluation system
表3. 河流健康评价指标体系
2.1.3. 评价标准
评价指标的标准参照国际及国家已经正式发布的标准和通过实际调查与理论分析综合确定的指标评价标准值 [13]。结合各指标特点,对每项指标划定5级,分别为I (理想状况)、II (健康)、III (亚健康)、IV (不健康)、V (病态)。指标层各项指标评价标准见表4。

Table 4. The criterion of each selected indicator
表4. 指标层各项指标评价标准
2.2. 模糊物元模型
2.2.1. 模糊物元
给定事物的名称N,它关于特征C有量值为V,以有序三元R(N,C,V)组作为描述事物的基本元,简称物元。如果物元模型中量值V具有模糊性,便称它为模糊物元。如果m个事物的n维物元组合在一起,使构成m个事物n维复合物元Rnm。若将Rnm的量值改写为模糊物元量值,称为m个事物n维复合模糊物元,记作
(7)
式中,Mj为第j个事物(
);Ci为第i个特征(
);vij为第j个事物第i个特征对应的模糊量值。
2.2.2. 从优隶属度模糊物元
各单项评价指标相应的模糊量值从属于标准方案中各对应评价指标相应的模糊量值的隶属程度,称为从优隶属度。根据从优隶属度计算公式对所有指标的原始值标准化,以消除量纲的影响。
由此可得到从优隶属度模糊物元
:
(8)
2.3. 熵权法确定指标权重
本文采用熵权法来确定河流健康评价中各个评价指标的权重。熵权法源于信息科学中的信息熵,其值用于反映信息的无序化程度,进而可以度量信息量的大小。若某项指标所含有的信息量越大,则表示该指标在评价体系中的作用也就越大。此方法可以避免权重赋值过程中主观性的影响。
3. 实例研究
3.1. 研究区域概况
淮河流域的地理位置处于长江和黄河之间,位于我国东部,东经范围111˚55'~121˚25',北纬范围30˚55'~36˚36',面积为27万km2,横跨山东省、河南省、安徽省、江苏省和湖北省 [16]。沙颍河作为淮河最大的支流,其位于南北气候的过渡带,冷暖气流频繁交汇,降雨分配不均,夏秋多,春冬少,洪涝干旱灾害易发生。经过近50年的建设,全流域兴建了大量的包括白龟山水库、周口闸等闸坝工程,显著地改变了流域的自然状况。
选取沙颍河上具有代表性的周口、界首和颍上断面来进行评价。研究区域概况见图1。
3.2. 评价模型建立
3.2.1. 指标数据计算
本文将选取沙颍河上具有代表性的周口、界首和颍上断面作为河流健康评价的评价对象,选取2017年为评估年。指标数据主要通过收集2017年的水文资料、相关报告和监测资料等获得。
3.2.2. 熵值法确定指标权重
计算得到各评价指标的权重见表5。
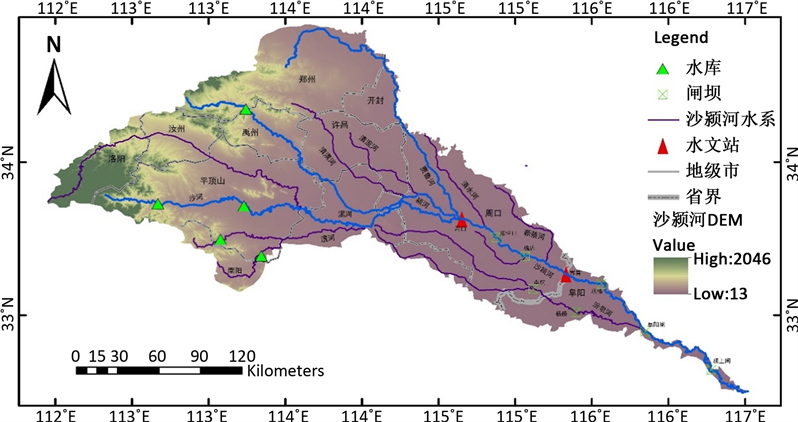
Figure 1. Sketch map of the Shaying River basin
图1. 沙颍河流域概况图

Table 5. Weight values of each evaluation indicator
表5. 各评价指标的权重值
3.2.3. 计算关联度
计算得到沙颍河代表断面的关联度
如下:
(9)
3.3. 结果和讨论
根据计算的关联度结果,本文将周口、界首和颍上断面的关联度值与分类标准I~V的关联度值相比较,可得到周口、界首和颍上三个断面的评价等级均为III级(亚健康),说明沙颍河干流的河流健康程度为良好,但是还有可以提高的空间。
3.3.1. 指标的建立
河流健康评价一个重要的步骤就是建立一个合理的评价指标体系。这个体系既能考虑研究区域的实际情况和现有的资料,又能尽可能地覆盖到河流的主要功能。本次指标建立首先依据河流的自然和社会属性,将指标分为两大类,第一类涵盖河流的主要自然属性,分别为反应径流和水量的水文水资源指标,反应河流受污染状况的水质指标和反应河流生态系统的水生态指标。其中水生态的指标内容较之前的研究更加丰富,综合考虑了底栖动物、浮游动物和浮游植物的多样性。河流的社会属性主要考虑其对社会经济发展的贡献和人为活动对河流的干扰,因此结合已有的资料,共选取了通航水位保证率以及水资源开发利用率两个指标。
沙颍河流域从上游至下游修建了众多的闸坝,天然河川径流被破坏,河流受到人为高度调控 [17]。维持河流健康并不意味着河流要完全恢复至天然状态,新时期的河流健康应该是同时兼顾河流的自然属性和社会属性,在维持河流自然状况不被恶化的前提下,合理地发展社会经济。因此指标体系中纳入对河流社会服务的考虑是必要的。
3.3.2. 各指标的重要程度
针对表3的评价指标体系,利用熵权法得到了各指标的权重,如表5。从表中可以看出有机污染水质状况指标所占的权重最高,重金属污染状况所占权重最低,近乎为0,因为三个断面的重金属污染状况均为评价等级中I类的理想状态,所以这个指标在此研究中意义不大。
此外,结合3.1中对纳入河流社会服务功能的重要性分析的讨论,为了验证此必要性,本研究在剔除了社会属性的指标后,重新利用基于熵权法的模糊物元法对同样三个断面进行评价。得到其关联度值如下:
(10)
本文定义纳入社会服务功能的河流健康评价为情景一,不纳入时为情景二。由上述计算结果可得,情景二中颍上断面的健康状况评价等级有变化,被评价为IV类。情景一中颍上断面的高通航水位满足度和相对合理的水资源开发利用率体现了其对社会经济发展的正向贡献,因而评价等级较情景二中的高。同时,对于周口和界首断面来说,虽然情景一和情景二中的评价结果同样为III类,但是情景一的关联度值比情景二的更加贴近II类,即距离评价标准的“健康”更加接近。这说明纳入河流的社会服务功能,考虑河流对社会经济做出的贡献是非常必要的。
4. 结论
本文结合多闸坝河流的特点与实际,从反映河流功能的水文水资源、水质、水生态和社会服务功能4个方面入手,选取了共10项指标表征河流健康状况。评价指标加入了反映河流社会服务功能的相关指标,使得河流健康评价更加合理。论文结合沙颍河流域开展的实例应用研究表明,基于熵权法的模糊物元模型能够应用于多指标的河流健康综合评价。
在实例研究中,沙颍河流域选取断面的评价结果均处于“亚健康”水平,尽管相比评价标准IV (不健康)和V (病态)级的河流,沙颍河的河流健康状况较为良好,但“亚健康”状态属于“健康”和“不健康”之间的过渡状态,此状况下的河流健康状态不稳定且转变敏感,故河流健康管理工作仍不容忽视。研究结果对深入认识沙颍河流域的河流健康状态和制订合理的河流健康保护措施具有重要的参考价值。
基金项目
本研究得到了国家水体污染控制与治理科技重大专项(批准号:2017ZX07602-003)的资助。