基于分子动力学的脉管气体振荡模拟及实验研究

Pulse Tube Gas Oscillation Based on Molecular Dynamics Simulation and Experimental Research

摘要: 随着科学技术的快速更迭，脉管制冷机在低温领域中的应用越来越广泛。本文基于分子动力学，对脉管内高低压He气的振荡过程进行模拟仿真，针对压缩过程，研究了脉管轴向温度波、速度波、压力波及质量流波随时间的变化，并对不同充放气频率下脉管冷端温度随时间的变化进行了实验探究。结果表明：模型内各点气体温度、速度均以正弦波的形式随时间呈现周期性变化，温度波变化趋势同实验结果一致。模型冷热端压力、质量流相位差不同，说明微脉管自身具备调相能力。另外实验结果显示，脉管自身存在最佳充放气频率，适当增加频率值有利于脉管制冷机制冷性能的提高。

Abstract: With the rapid changes in science and technology, pulse tube refrigerators are more and more widely used in the field of cryogenics. Based on molecular dynamics, this paper simulates the oscillation process of the high and low pressure He gas in the pulse tube. Aiming at the compression process, the changes of the axial temperature wave, velocity wave, pressure wave and mass flow wave of the pulse tube over time are studied. The temperature change of the cold end of the pulse tube with time under the deflation frequency was investigated experimentally. The results show that the gas temperature and velocity at each point in the model change periodically with time in the form of a sine wave, and the changing trend of the temperature wave is consistent with the experimental results. The pressure and mass flow phase difference between the cold and hot ends of the model are different, indicating that the micropulse tube itself has the ability of phase modulation. In addition, the experimental results show that the pulse tube itself has the best charging and discharging frequency, and an appropriate increase in the frequency value is beneficial to the improvement of the cooling performance of the pulse tube refrigerator.

1. 引言

当前是一个科学技术快速发展的时代，技术更新或者升级每天都在发生。在低温制冷技术领域也是如此。其中脉管制冷机以体积小、冷端无运动部件、运行寿命长、可靠性高、振动小等优异特性在多个领域得以广泛应用。脉管制冷机是由Longsworth和Gifford首次发现提出的，并对此进行了深入研究，提出了表面泵热理论 [1]。起初，由于基本型脉管制冷机制冷效率低下，并未得到广泛应用。直到20世纪80年代初，Mikulin [2] 等人研制出了小孔 + 气库型脉管制冷机，打破了脉管制冷机的僵局，获得了更低的制冷温度。1994年，Kanao [3] 发明了惯性管 + 气库型结构，进一步提高了脉管制冷机的性能，此后被广泛应用于实践之中。在之后的研究中，各种调相型脉管制冷机(如多路旁通型脉管制冷机 [4]、主动气库调相型脉管制冷机 [5]、双活塞型脉管制冷机 [6] [7])的出现，更是脉管制冷机发展历程上的突破。

虽然脉管制冷机在近年来取得了重大的发展，但由于脉管制冷机在运行时涉及到热力学知识、流体动力学知识、传热学知识等，且其内部伴有较为复杂的流动过程，因此脉管内部制冷机理的研究至今还不完善。近年来，关于脉管制冷机理的研究也在不断拓展。Chao Gu [8] 等人通过CFD模拟的方法，首次运用计算流体动力学方法研究了脉管制冷机中的第三类流动，发现在脉管制冷机内部，流体的非线性流动和传热性质均会影响制冷温度和制冷性能。A. Jafarian [9] 等人运用数值模拟的手段，通过控制容积方法预测了大容量脉管制冷机的流动力学和热力学性质，并且表明脉管制冷机的运行参数是影响其制冷效率的主要因素之一。王亚男 [10] 等人基于Sage软件对VM制冷机进行整机模拟，以无负荷制冷温度最低为目标函数，研究了平均压力、频率和热压缩机冷端温度等运行参数对制冷机性能的影响。Amin Kardgar [11] 等人采用数值模拟方法，研究轴向热传导对脉管制冷机中脉管部分，发现振荡流对共轭传热的影响。张玲丽 [12] 等人利用Fluent软件对惯性管加气库型脉管制冷机进行数值模拟，分析了不同工作频率下，不同连接方式对惯性管工作性能的影响。Chen Liubiao [13] 等人通过数值模拟加实验的方法对气体耦合型斯特林脉管制冷机进行了研究，分别就冷端换热器材料、直径、惯性管尺寸对质量流量的影响进行了分析。本文一方面是采用分子动力学计算方法，从微观角度模拟脉管模型内部气体交变振荡过程；另一方面，通过试验台的搭建，从宏观角度，对模拟结果进行验证分析。

2. 脉管制冷机热力学性质

Figure 1. Temperature distribution of compression and expansion of basic pulse tube

图1. 基本型脉管压缩、膨胀温度分布图

图1为气体在脉管制冷机内部交变流动过程中制冷机内各部分温度分布图。首先研究气体压缩过程，制冷机内高压气体高速流过回热器时，气体迅速被冷却至T_c，气体在进入冷端换热器时可以达到制冷的效果。随后气体流经层流化元件，此后，气体以层流的状态进入脉管，并以此状态继续向前运动。在达到脉管封闭端时，由于后续气体仍不断向前运动，致使气体不断被压缩，温度升高，脉管末端温度升高到T_m。至此，为脉管制冷机的压缩过程。在封闭端处，采用循环冷却水冷却的方式，使末端温度降到T_a。其次讨论制冷机放气膨胀过程，图中虚线表示膨胀过程制冷机各部分温度分布。管内高压气体不断流出，气体膨胀导致温度降低，气体流至冷端换热器时，温度降至T_i，T_i < T_c，此时，气体从外界(T = T_c)吸收能量，达到制冷的效果。流出脉管的气体，经过回热器加热升温后，又重新进入压缩机，如此往复进行压缩、膨胀过程。实现制冷的目的。

3. 分子动力学

分子动力学模拟方法目前被广泛应用于计算大型复杂系统。近年来，由于力学的迅速发展，建立了适用于生化分子体系、聚合物、金属与非金属等不同领域的力场，这些力场大大提升了计算结果的精确度。分子动力学模拟方法是基于这些力场和牛顿力学而衍生出的一种新型计算方法。

对于多原子系统，系统能量为系统中原子动能与系统总势能之和。总势能为

$U=U_{VDM}+U_{\mathrm{int}}$ (1)

式中，U原子间总势能； $U_{VDM}$ 为非键结范德瓦耳斯作用力； $U_{\mathrm{int}}$ 为分子内部势能。

依照经典力学知，系统中原子所受的势能梯度：

$F_i=-{\nabla }_{i}U=-\left(i\frac{\partial }{\partial x_i}+j\frac{\partial }{\partial y_i}+k\frac{\partial }{\partial z_i}\right)U$ (2)

式中， $F_i$ 为i原子所受的力。

由牛顿运动定律可得i原子的加速度为：

$a_i=\frac{F_i}{m_i}$ (3)

式中， $a_i$ 为i原子的加速度；m_i为i原子的质量。

$\frac{{\text{d}}^2}{\text{d}{t}^2}{r}_i=\frac{\text{d}}{\text{d}t}{r}_i=a_i$ (4)

$v_i=v_i^0+a_{i}t$ (5)

$r_i=r_i^0+v_i^{0}t+\frac{1}{2}{a}_i{t}^2$ (6)

式中， $r_i$ 和 $r_i^0$ 分别是i原子现在位置和初始位置； $v_i$ 和 $v_i^0$ 分别是i原子现在速度和初始速度。

本次模型旨在研究脉管制冷机压缩时高低压He气的自振荡过程。首先进行模型的建立，根据理想气体状态方程PV = NRT，计算低压端(100 kPa) He原子(R = 0.122 nm)流体介质的稳态模型。确定低压端He原子数为9000，模型尺寸：8581.8 Å (X) × 14.303 Å (Y) × 3000 Å (Z)，即长度为858.18 nm，宽度为1.4303 nm，高度为300 nm。然后用同样的方法计算、建立高压端(600 kPa) He原子流体介质稳态模型，He原子数为54,000，其中高低压端He气初始温度均设为300 K。最后，采取对局部模型拼接的方法，就可拼接成完整模型。最终创建的模型如图2所示，模型尺寸为17,163.6 Å (X) × 14.303 Å (Y) × 3000 Å (Z)。对于放气模型只需要将He气高低压空间对调即可，机理类似。

Figure 2. 3H-6L basic pulse tube model

图2. 3H-6L基本型脉管模型

4. 力场及势函数描述

本模拟所用力场为混合力场，选用lj/cut势能。He-He原子之间通常选用的势能函数为方程(7)的UFF函数 [14]，其内部变量参数固定，如表1所示。

$E=D_O\ast \left[{\left(\frac{R_O}{R}\right)}^{12}-2{\left(\frac{R_O}{R}\right)}^{12}\right]$ (7)

Table 1. UFF potential energy parameter

表1. UFF势能参数

势能函数设定完成后，首先让系统在正则系综NVT (粒子数N、体积V、温度T)下运行一定的步长，对系统初始温度进行标定，使初始温度稳定在300 K；其次，接着NVT的计算结果，使模型在微正则系综NVE (粒子数N、体积V、总能E)下运行，至整个系统内部气体混合均匀，即可结束运行。

5. 模拟结果分析

对图2所示3H-6L模型在轴向方向上进行网格划分，利用Fortran程序统计不同时间段模型网格内He原子压力、温度、速度等随时间的变化过程。

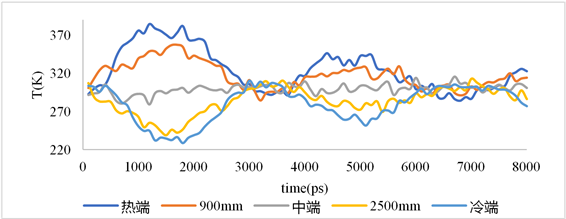
Figure 3. The temperature variation diagram of each point in the compression process model with time

图3. 压缩过程模型内各点温度随时间变化图

图3为压缩过程模型内部各点温度随时间变化过程图。从图中可以看出，热端温度以正弦的形式呈周期性变化，冷端则呈负正弦变化。温度振荡波逐渐衰减，冷热端温度的最值出现在第一个四分之一周期处，这是因为整个模拟仅靠初始压差驱动，是一个自振荡过程，温度波会随着振荡周期的增加而逐渐衰减。

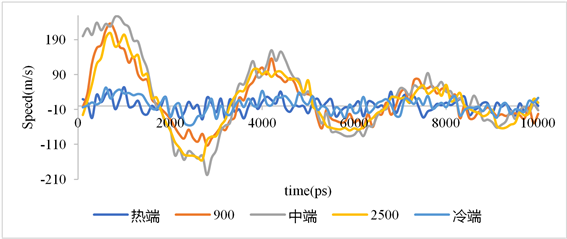
Figure 4. The velocity variation diagram of each point in the compression process model with time

图4. 压缩过程模型内各点速度随时间变化图

图4为压缩过程模型内部各点速度随时间变化图。从图中可以清晰的看出，速度波也以正弦波的形式呈周期性衰减。针对模型内部各点进行分析，可以发现，模型中端附近初始速度及速度振幅最大，这是因为初始时刻，中端位置位于高压气体与低压气体的交界处，压差导致了气体的快速运动。随着压缩过程的进行，系统整体压力差趋于稳定。但由于气体自身的惯性作用，气体继续向低压端移动，至出现原低压端气体压力高于高压端，使气体出现反向加速度。气体微团开始减速，之后开始逆向运动。由于压差的衰减，下一个周期速度的峰值低于首次出现的速度峰值。因为模型内部压差及气体自身惯性的作用，内部各点呈逐渐衰减的周期性振荡。模型两端的速度变化不大，始终在0附近波动，这是因为模型两端壁面固定的原因。可见，若按照第一周期气体自振荡频率给与制冷机压力波，气体振荡将保持在最佳状态，有利于制冷机性能的提高。

(a) 冷端(b) 热端

Figure 5. Phase contrast diagram of pressure wave and mass flow wave

图5. 压力波、质量流量波相位对比图

图5为模型压缩过程冷、热端压力波和质量流量波相位对比图。取压力波超前质量流波为正，经计算得，模型冷端相位差为70度，热端为−78.75度，出现了反相位关系，微尺寸脉管显示出了自身的调相能力，这也是微尺寸脉管相比于普通脉管的一大优势。利用分子动力学仿真方式可获取脉管内各微元处的相位分布情况，为研究微型尺寸脉管内不同的相位分布情况提供了预测方法。

6. 实验分析

Figure 6. Schematic diagram of single-stage G-M pulse tube refrigerator

图6. 单级G-M型脉管制冷机示意图

图6为单级G-M型脉管制冷实验台示意图。用高低压气源代替压缩机，电磁阀的转换来实现气体振荡。电磁阀转向高压气源时，为充气过程，高压气源中气体进入回热器，再流入脉管。当电磁阀转向低压气源，这部分气体流向低压气源，实现放气过程，这样来回充放气实现脉管中气体振荡。试验台布置三个温度点(热端换热器1、冷端回热器和热端换热器2)来检测温度。

本实验设定高压气源压力1.2 MPa，低压气源100 MPa，脉管尺寸：∅4 mm * 85 mm，分别对充放气频率为0.5 Hz，1 Hz，2.5 Hz，5 Hz情况进行实验探究。

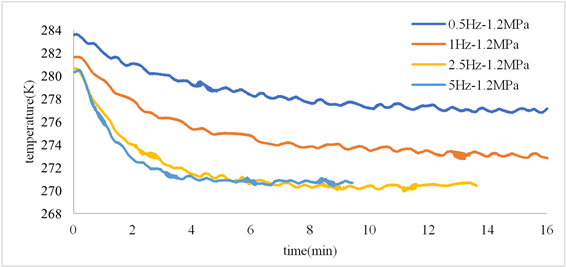
Figure7. Variation diagram of cold end temperature with time in pulse tube experiment

图7. 脉管实验冷端温度随时间变化图

图7所示为在各个充放气频率下，脉管冷端温度变化结果。可以看出，对应不同充放气频率，脉管制冷机存在不同的温降。在较小的频率范围内，随着充放气频率的提高，脉管制冷机冷端温降越来越大，同时温度的变化速率呈现越来越快的趋势。但达到一定的频率值以后，温降以及温度速率变化不再那么明显。实验结果表明针对不同的制冷工况，存在最佳充放气频率值，选择合理的脉管制冷机充放气频率是很有必要的，在适当的范围内，增加充放气频率，有利于制冷机制冷性能的提高。但达到最佳频率值以后，频率的增加对制冷效果的影响不那么显著，另外从能源角度考虑，反而会增加多余的能耗。

对脉管制冷机在各个充放气频率实验结果进行局部放大，分别见图8(a)~(d)，显然，温度呈周期性振荡波动，呈正弦波变化。即冷端温度以正弦曲线振荡的形式下降。相比于模拟结果，实验结果显示制冷机冷端整体温度变化存在一个明显的下降的过程，这是由于G-M制冷机给了持续的外界驱动压力，而模拟的脉管温度变化是基于初始压力差的自振荡过程。但温度的周期性振荡变化结论与模拟结果基本相符。

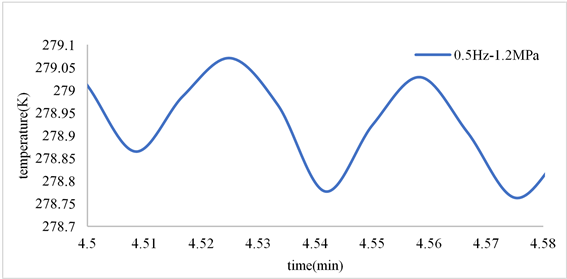(a) 0.5 Hz~1.2 MPa 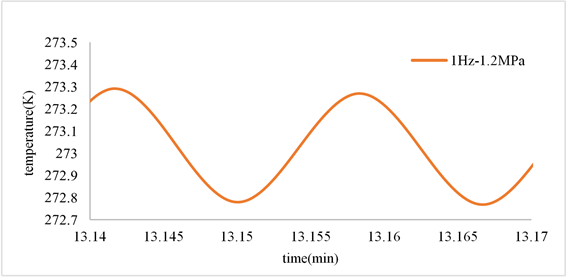(b) 1 Hz~1.2 MPa (c) 2.5 Hz~1.2 MPa 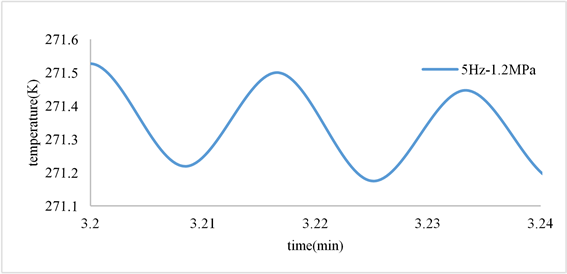(d) 5 Hz~1.2 Mpa

Figure 8. Variation curve of temperature at the cold end of the pulse tube with time at various frequencies

图8. 各频率下脉管冷端温度随时间的变化曲线

7. 结论

采用分子动力学计算方法，对脉管内He气工质交变振荡过程进行了模拟仿真，并从宏观角度，通过实验的方法进行了验证分析。结果表明，模拟的脉管冷端温度变化过程以正弦的形式呈周期性振荡，模拟结果与实验结果基本相符。这说明了，模拟虽然是在微尺寸下进行的，但不受尺寸效应影响，具有可信性。通过模拟高低压气体的运动，对管内气体速度分布随时间的变化情况进行分析，结果显示，同温度变化情况相同，速度的变化亦呈周期性振荡，并不断衰减，这是气体运动时自身的惯性作用及高低压气体压差作用的结果。通过对比冷热端压力、质量流相位发现，冷热端相位差发生了较大的变化，显示了脉管自身的调相能力。另外，实验研究了同一压比，不同充放气频率下G-M脉管制冷机冷端温度随时间的变化情况，实验结果表明，对某一制冷工况，脉管制冷机存在最佳的充放气频率，在一定的频率范围内，适当地增加充放气频率，有利于G-M制冷机性能的提高。

基金项目

上海市动力工程多相流动与传热重点实验室项目(13DZ2260900)。