用于无人机巡线的图像分类模型选择算法研究

Research on Algorithm of Image Classification Model Selection for UAV Patrol

摘要: 随机森林算法作为经典的分类算法，应用广泛，分类的准确度高。但在分类的过程之中，各个决策树的分类性能和两两决策树之间的差异性是影响最终分类效果的两个重要因素，当部分决策树有相似的错误分类情况，在最终利用决策树的结果进行投票时，将降低模型最终的分类效果。针对该问题，本文将误差矩阵引入分类树的相似性度量当中。该方法考虑了不同类别的树的数量、分类正确错误的情况，以便选出相似度弱的决策树，然后，剔除分类能力差的决策树，最终选择出分类能力强的分类器集合。实验结果显示，本文提出的方法在3类数据集中，平均分类正确率高于原算法，且稳定性更高。

Abstract: As a classic classification algorithm, random forest algorithm is widely used and has high classification accuracy. However, in the process of classification, the classification performance of each decision tree and the difference between two decision trees are two important factors that affect the final classification effect. When some decision trees have similar misclassifications, and they are used in the final voting on the results of the decision tree, the final classification effect of the model will be reduced. Aiming at this problem, this paper proposes a method for measuring the similarity of decision trees based on confusion Matrix. This method takes into account the number of different categories of trees and the correct and incorrect classification, in order to select decision trees with weak similarity, and then remove the decision trees with poor classification results, and finally complete the model selection of random forest. Experimental results show that the method pro-posed in this paper has a higher average classification accuracy rate and higher stability in the three types of datasets.

1. 引言

随着无人机电力线路巡检的发展，无人机拍摄了大量的图像信息，数据将增长非常快，目前已经发展到了几个PB的海量数据。为了便于处理数据，各种分类算法层出不穷。其中，随机森林算法是以分类集成思想为基础的回归模型。该算法被应用于气象分析 [1]、医学 [2]、大数据推荐 [3] 等。由于随机森林良好的分类能力，也被用来进行数据的处理，并应用于分布式当中 [4] - [9]。该算法被进行多次改进。如通过将新的理论引入随机森林，得到算法效果的提升。文献 [10] [11] 将随机森林算法与Hough Transform相结合，应用于目标检测，效果较好。文献 [12] 把survival forests与随机森林相结合，提升了算法的性能。谢晓东 [13] 等利用梯度提升算法森林模型进行了改进，提高了模型的分类准确性。魏正涛 [14] 通过对抽样结果增加约束条件来改进重抽样方法，加强了算法的分算类能力。王诚 [15] 等对随机森林算法中存在的面对特征纬度高且不平衡的数据时，算法性能低下的问题提出了改进的算法。该算法先对数据集的特征按照正负类分类能力赋予不同的权值，然后删除冗余的低权值的特征值，得到性能良好的特征子集构造随机森林。文献 [16] 使用聚类的方法，将效果良好的分类器进行聚合；文献 [17] 将基分类器进行划分，选择出效果良好的分类器。通过筛选出来的决策树进行最终的投票过程中，如果各个决策树的相似性过高，决策树的种类过于单一，那么最终的分类效果会变差。同时，现有的决策树选择策略带来的计算量比较复杂，分类效果欠佳。为了解决该问题，本文将误差矩阵引入随机森林算法中，删选出种类更多的决策树，提升了随机森林算法的分类能力。

2. 集成学习

集成分类器的差异性度量

集成学习，即集成分类器，指的是通过构建若干分类器，然后用某种方法将这些分类器的分类结果结合起来进行学习，完成任务。

集成分类器有两种方式进行分类。第一种是选择不具有强依赖关系的分类器进行学习，该方法将分类器进行综合和分析较为困难。第二种是选择有依赖关系的分类器进行学习，对于大多数分类方法都倾向于该方法。对于总的分类器的错误率和单分类器错误率之间的关系 [18]，如公式(1)所示。

$E_{total}=E_{bay}+\frac{1+\rho \left(N-1\right)}{N}{E}_{each}$ (1)

其中， $E_{total}$ 及 $E_{each}$ 分别代表总的错误率和单分类器的错误率， $\rho$ 表示单分类器的错误相关性，N是总分类器的规模， $E_{bay}$ 是基于已知分布和Bayes规律的分类错误率。

对于差异性的度量有两种方法。第一种是非成对差异性度量，即直接计算集成系统的差异性值。第二种是成对差异性度量，通过计算每一对分类器的差异性值，然后用平均值衡量总的差异值。常用的方式 [19] [20] 有分歧度量，双误度量、评判间一致度 [21] 等。本文采用的就是第二种方法。

3. 随机森林算法

随机森林算法具体的步骤如下所示。

1) 从训练集中采用bootstrap法，即自助抽样法，有放回地抽取若干样本，作为一个训练子集。

2) 对于训练子集，从特征集中无放回地随机抽取若干特征，作为决策树的每个节点的分裂的依据。

3) 重复步骤1)和步骤2)，得到若干训练子集，并生产若干决策树，将决策树组合起来，形成随机森林。

4) 将测试集的样本输入随机森林中，让每个决策树对样本进行决策，得到结果后，采用投票方法对结果投票，得到样本的分类结果。

5) 重复步骤4)，直到测试集分类完成。

4. 随机森林模型选择

4.1. 本文提出的模型选择方法

本文提出一种基于误差矩阵的随机森林改进方法，主要思想在于将误差矩阵引入决策树的相似性度量方法中，以删选出合适的分类树。随机森林算法的总流程如图1所示，本文重点是利用误差矩阵对决策树就进行删选。

4.1.1. 基于误差矩阵判断分类树相似性

判断两棵分类树相似度的方法通常主要有两类，第一种是根据两棵树之间的结构的差异性来判断相似性，常用的方法是利用一些算法 [22] 直接判断结构的差异性，通常该方法的计算量较大。第二种是通过分类树的分类结果来判断相似性。如果两棵树的分类准确率相近则认为是相似的，或者两棵树对样本集进行分类时，将其分在同一类，也认为是相似的。本文采用的是第二种方法，即将分类结果中类别之间的关系进行分析，在分类树的误差矩阵上进行相似性的判别。

误差矩阵常作为分类结果的可视化工具 [16]，在监督学习中应用广泛。对于误差矩阵，每一列代表数据的预测类别，每一列的总数代表预测为该类别的样本的数目，每一行代表数据的真实归属类别。每一行的总数表示该类别的数目。 $X=\left\{x_1,x_2,\cdots ,x_N\right\}$ 表示N个样本数据， $Y=\left\{y_1,y_2,\cdots ,y_M\right\}$ 表示M种分类的类别，通过矩阵 $CN$ 表示N个样本数据在分类之后的结果，如公式(2)所示。

$CN=\left[\begin{array}{ccc}c{n}_{11}& \cdots & c{n}_{1m}\\ ⋮& c{n}_{ii}& ⋮\\ c{n}_{m1}& \mathrm{...}& c{n}_{mm}\end{array}\right]$ (2)

式中 $c{n}_{ij}$ 表示样本数据X中真实类别为i的数据被分为类别j的数据的总数量。显然 $c{n}_{ii}$ 表示的是类别为i的数据被正确分类的数量。

本文使用矩阵的距离测度和向量夹角作为两棵树的相似性度量。当分类树类似时，则矩阵就相接近。同理，当矩阵距离较远，则分类树的差距就较大。

差值矩阵 $DC{N}^{\left(i,j\right)}$ 是两个误差矩阵 $C{N}^{\left(i\right)}$ 和 $C{N}^{\left(j\right)}$ 之差( $i,j$ 代表两棵决策树)。 $DC{N}^{\left(i,j\right)}$ 的大小是 $M\times M$，如公式(3)所示。

$DC{N}^{\left(i,j\right)}=C{N}^{\left(i\right)}-C{N}^{\left(j\right)}=\left[\begin{array}{cccc}c{n}_{11}^{\left(i\right)}-c{n}_{11}^{\left(j\right)}& c{n}_{12}^{\left(i\right)}-c{n}_{12}^{\left(j\right)}& \cdots & c{n}_{1N}^{\left(i\right)}-c{n}_{1M}^{\left(j\right)}\\ c{n}_{21}^{\left(i\right)}-c{n}_{21}^{\left(j\right)}& c{n}_{22}^{\left(i\right)}-c{n}_{22}^{\left(j\right)}& \cdots & c{n}_{2N}^{\left(i\right)}-c{n}_{2M}^{\left(j\right)}\\ ⋮& ⋮& \ddots & ⋮\\ c{n}_{M1}^{\left(i\right)}-c{n}_{M1}^{\left(j\right)}& c{n}_{M2}^{\left(i\right)}-c{n}_{M2}^{\left(j\right)}& \cdots & c{n}_{MM}^{\left(i\right)}-c{n}_{MM}^{\left(j\right)}\end{array}\right]$ (3)

当不同类别的样本的数量有较大的差距时，数量大的类别会影响到矩阵距离的计算，最终使随机森林分类器更多地趋于多值类别。因此，考虑到这个因素，本文使对差值矩阵 $DC{N}^{\left(i,j\right)}$ 进行归一化处理，得到矩阵 $DC{N}_u^{\left(i,j\right)}$，其元素为 $dc{n^{\prime }}_{mn}$，具体的计算如公式(4)、(5)所示。

$dc{n^{\prime }}_{mn}=\frac{dc{n}_{mn}}{ma{x}_m}$ (4)

$ma{x}_m=ma{x}_n\left(dc{n}_{mn}\right)$ (5)

其中 $ma{x}_m$ 表示差值矩阵第m行的最大值。

定义规模为l的随机森林的相似性度量矩阵为 $R_F$， $R_F$ 的大小和树的数量有关，是的方阵。其元素 $r{f}_{ij}$ 与归一化差值矩阵 $DC{N}_u^{\left(i,j\right)},i,j=1,\cdots ,l$ 的关系如公式(6)所示。

$r{f}_{ij}=\{\begin{array}{l}0,\left(i\ge j\right)\\ {\Vert DC{N^{\prime }}_{i,j}\Vert }_F=\sqrt{{\displaystyle {\sum }_m^M{\displaystyle {\sum }_n^{M}dc{n^{\prime }}_{mn}^2}}},\left(i<j\right)\end{array}$ (6)

当 $r{f}_{ij}$ 越小，则树i与树j的相似度越高，两个分类器对样本的分类结果越接近。

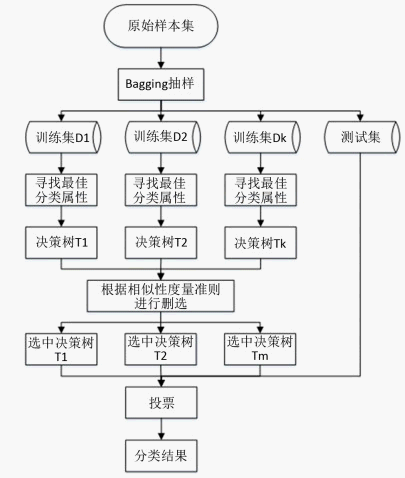
Figure 1. Random forest selection model

图1. 随机森林选择模型

4.1.2. 基于“删劣”策略选择模型

对于常用选择策略，采用的是选优策略，即从分类器之中选择出若干代表性强的分类器。这种方法对分类器的分类效果和分类器之间的关联性都有要求，是多对多的关系，因此用该方法进行选择较为复杂 [23]。本文选择另一种方法，即删除效果不佳的分类器。从基础分类器之中将相关度高的，分类能力差的分类器删除，然后将剩下的分类器集中在一起，组成新的模型。

这种删除策略只需要应用于相关度高的分类器之间，当相关度超过所设的阈值时，就将其剔除，因而该方法计算量将大大降低计算量。同时该方法还降低了总体分类器之间的相关度，从而提升分类能力。

4.1.3. 模型选择算法描述

具体步骤如算法1所示。

算法1随机森林模型选择算法

输入：决策树相似度阈值t、分类准确度阈值 $\beta$

输出：随机森林模型RF

1：通过决策树对测试样本进行分类预测；

2：根据分类结果，为决策树创建误差矩阵 $CN$

3：创建相似度度量矩阵 $R_F$ ：

4：for (( $i,j=1$ to l) & ( $i<j$ ))

利用公式(3)计算 $DC{N}^{\left(i,j\right)}$

利用公式(4)和公式(5)计算 $DC{N}_u^{\left(i,j\right)}$

利用公式(6)计算 $DC{N}_u^{\left(i,j\right)}$ 的范数，即 $R_F$ 在该处的元素值

5：令 $m_{ij}$ 为 $R_F$ 中最小的非零元素

6：for ( $m_{ij}<t$ )

if (决策树i分类效果 $<\beta$ )

将 $R_F$ 中的树i清除

$m_{ij}=$ $R_F$ 中下一个最小非零元素

7：否则结束，未删除的决策树组成随机森林RF。

5. 实验与分析

5.1. 实验数据说明

本文使用的数据集是UCI机器学习数据集的部分数据，具体信息如表1所示。

Table 1. Experimental data set taken from UCI

表1. 取自UCI的实验数据集

5.2. 实验结果与分析

本实验通过从10到100内，不同的十个随机森林规模，然后对原始的随机森林(RF)和基于误差矩阵的随机森林(CM-RF)的分类结果进行对比采用的指标为平均分类准确率。实验结果如图2~4示。

由实验结果看出，对于iris和anneal数据集，在初始树规模不同的情况下，基于误差矩阵的随机森林的平均分类准确率均高于传统的随机森林模型。对于glass数据集，随着随机森林在建数目的增加，传统的随机森林算法和本文提出的模型都出现了分类准确率下降的情况，但是，基于随机矩阵的森林的分类准确率下降更加缓慢，从而本文算法保持了一定的鲁棒性。因此，进一步说明本文提出的基于误差矩阵的随机森林模型的有效性。

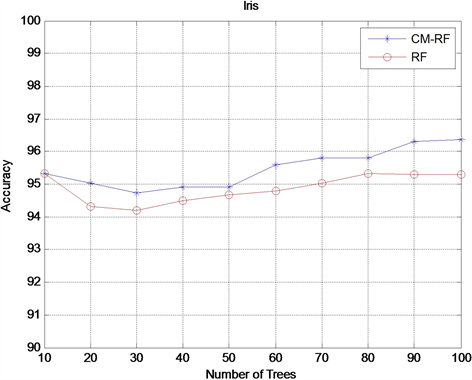
Figure 2. Accuracy comparison results on the Iris dataset

图2. Iris数据集上Accuracy对比结果

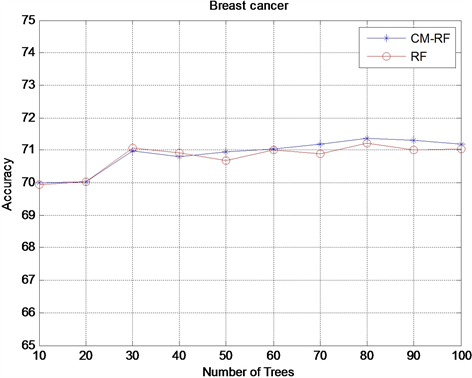
Figure 3. Accuracy comparison results on the Breast-cancer dataset

图3. Breast-cancer数据集上Accuracy对比结果

Figure 4. Accuracy comparison results on the Aneal dataset

图4. Aneal数据集上Accuracy对比结果

6. 结束语

本文提出了一种基于误差矩阵的随机森林分类模型选择方法。将误差矩阵应用于决策树的相似性度量中，通过使用矩阵的距离测度和向量夹角判断两棵树的相似性，考虑到树的数量占比问题，对矩阵每行进行归一化处理，之后结合决策树的分类性能，采用“删劣”思想完成随机森林模型的选择。由实验结果可知，该方法提高了分类的准确度。

基金项目

赛尔网络下一代互联网技术创新项目(NGII20170104)。