基于正负类边界距离的多标签数据属性约简

Attribute Reduction for Multi-Label Data Based on Boundary Distance between Positive and Negative Classes

摘要: 本文首先将多标签分类问题分解为一系列单标签二分类子问题，每一个子问题对应一个标签。子问题的正类定义为具有该标签的样本，负类定义为不具有该标签的样本。在给定的属性子集下，计算出正负类样本之间的最小距离，即分类边界的最小距离。将子问题分类边界最小距离求和定义为依赖度函数，并将此依赖度函数作为属性子集重要度评价指标。然后建立了所提出依赖度函数关于属性子集的单调性，并通过最大化依赖度函数给出了属性约简的定义。最后，设计了一种基于正负类边界距离的属性约简算法，并在实际的多标签数据集上进行了实验，实验结果表明，所提约简算法能够建立合理的属性重要度排序，有效地去除冗余属性。

Abstract: In this paper, the multi-label classification problem is decomposed into a series of single-label bi-nary classification sub-problems, each of which corresponds to one label. The positive class of the sub-problem is defined as the sample with the label, and the negative class is defined as the sample without the label. Under the given attribute subset, the minimum distance between positive and negative class samples is calculated, that is, the minimum distance of classification boundary. The sum of the boundary distances for all sub-problems is defined as dependency function, which is used as the evaluation of the importance of the attribute subset. The monotonicity of the proposed dependence function with respect to the attribute subset is established, and the definition of the attribute reduction is given by maximizing the dependence function. Finally, an attribute reduction algorithm based on positive and negative class boundary distance is designed, and the experiments are carried out on actual multi-label data sets. The experimental results show that the proposed algorithm can establish a reasonable ranking of attribute importance and effectively remove redundant attributes.

1. 引言

近年来，在数据挖掘和机器学习领域中，多标签分类问题引起了广泛的关注。多标签分类和单标签分类的区别就是单标签分类中的样本只能与一个标签相关联，而多标签分类中的样本可能同时与多个类别标签相关联 [1] [2] [3]。

在多标签数据中，有些属性可能是冗余的或与分类任务不相关的，冗余或不相关的属性会导致多标签分类器的分类性能较差。因此，在设计分类器前，需要减少冗余或不相关的属性 [4]。属性约简就是在分类能力不变的前提下，删除其中冗余或不相关的属性，选择一个最优属性子集来提高分类器的分类性能，保留了数据集最有用的信息，使分类模型简洁，具有更好的泛化能力 [5] [6] [7]。

属性约简是多标签分类重要的数据预处理过程，其目的是减少数据的维数，来提高数据处理速度 [8]。2018年，Lin等人提出了一种新的模糊粗糙集模型，采用局部采样技术构造样本间的鲁棒距离，并建立了一种适用于多标签学习的属性约简算法 [9]。2019年，Wang等人提出了一种基于信息论的多标签学习特征选择算法，他先定义了多标签信息熵和多标签互信息的新概念，然后，建立了一种缺失标签的多标签特征选择方法 [10]。2020年，Liu等人通过设计类间判别和类内邻域识别来选择每个新到达的标签特征，提出了一种在流标签环境下的多标签特征选择方法 [11]。

现有的属性约简算法，计算复杂度较高，而样本间距离运算简单，直观，所以我们在这篇论文中利用样本间距离，定义依赖度函数，使模型更加简洁，运算速度更快。我们首先将多标签分类问题转化为二分类问题，并介绍了正负类样本集，然后，求出正负类样本间距离，从而定义了依赖度函数。通过正负类样本间距离函数，证明了依赖度函数相对于属性子集是单调递增的。接着给出了属性约简定义，最后，设计了一种基于正负类边界距离的属性约简算法，来选择最优的多标签属性子集。为了验证该方法的性能，我们将其与现有的四种多标签特征选择算法进行了比较。实验结果表明，该方法能够有效地去除冗余属性。

论文的其余部分结构如下。在第一节中，回顾了多标签分类的基础知识、点到点的距离、集到集的距离和点到集的距离的定义。在第二节中，我们给出了属性约简的定义，设计了一种基于正负类边界距离的属性约简算法。在第三节中，汇报了我们的算法在9个多标签数据集上实验的结果。在第四节中，对本文所得结论和实验结果进行总结，并提出了今后要研究的问题。

2. 基础知识

多标签数据表示为 $S=\left(U,A,L\right)$，其中样本集 $U=\left\{x_1,x_2,\cdots ,x_n\right\}$ 是一个非空有限集，表示有n个样本实例。属性集 $A=\left\{a_1,a_2,\cdots ,a_p\right\}$ 是一个非空有限集，每个属性 $a\in A$ 是从样本集U到实数集的函数，其中 $a\left(x\right)$ 表示为样本 $x\in U$ 在属性a上的值。标签集 $L=\left\{l_1,l_2,\cdots ,l_q\right\}$ 是一个非空有限集，表示有q个标签。每个标签 $l\in L$ 被定义为从样本集U到集合 $\left\{\text{0,1}\right\}$ 的函数。假设样本x与标签l相关联，则 $l\left(x\right)=1$ ；否则， $l\left(x\right)=\text{0}$。

对于任意非空属性子集 $B\subseteq A$，假设样本点x和点y都是样本集U中的点，则点x和点y之间的距离定义为

$d_B\left(x,y\right)={\displaystyle \underset{a\in B}{\sum }\left|a\left(x\right)-a\left(y\right)\right|}.$

对于每个非空属性子集 $B\subseteq A$，设集合X和集合Y是样本集U的子集，则集合X和集合Y之间的距离定义为

$d_B\left(X,Y\right)=\underset{x\in X,y\in Y}{\min }{d}_B\left(x,y\right).$

当集合X是单点集 $\left\{x\right\}$ 时，点x和点集Y之间的距离为

$d_B\left(x,Y\right)=\underset{y\in Y}{\min }{d}_B\left(x,y\right).$

任意两个非空集X和Y都有 $d_B\left(X,Y\right)\ge 0$。

3. 多标签数据属性约简

在给定标签 $l_i\in L$ 的情况下，关于 $l_i$ 的一对样本集被定义为

$E_i=\left\{x\in U:l_i\left(x\right)=1\right\},i=1,\cdots ,q.$

$F_i=\left\{x\in U:l_i\left(x\right)=\text{0}\right\},i=1,\cdots ,q.$

样本集 $E_i$ 是有该标签的样本集合，样本集 $F_i$ 是没有该标签的样本集合， $E_i$ 是正类样本集， $F_i$ 是负类样本集。每个标签具有一对样本集 $E_i$ 和 $F_i$。对于给定的属性子集 $B\subset A$，下面的函数 $d_B\left(E_i,F_i\right)$ 可以测量正类样本集 $E_i$ 和负类样本集 $F_i$ 之间的距离，函数定义为

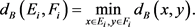
这个距离函数 $d_B\left(E_i,F_i\right)$ 测量了正类样本集 $E_i$ 和负类样本集 $F_i$ 的边界距离，函数值越大，分类器的分类能力越好。也就是说，标签相同的样本距离越近越好，标签不同的样本距离越远越好。

定义1：对于任意非空属性子集 $B\subseteq A$，我们将每个标签的正负类样本间距离求和定义为依赖度函数，依赖函数为

$\gamma \left(B\right)={\displaystyle \underset{i=1}{\overset{q}{\sum }}{d}_B}\left(E_i,F_i\right)$

依赖度函数 $\gamma \left(B\right)$ 用于评估属性子集的重要性，依赖度函数值的大小取决于正负类样本间距离函数 $d_B\left(E_i,F_i\right)$ 值的大小。

引理1：对于多标签数据 $S=\left(U,A,L\right)$，距离函数 $d_B\left(E_i,F_i\right)$ 和依赖度函数 $\gamma \left(B\right)$ 相对于属性集B是单调递增的。任意选择两个属性子集 $B_1$ 和 $B_2$，有 $B_1\subset B_2\subset A$，则存在 $d_{B_1}\left(E_i,F_i\right)<d_{B_2}\left(E_i,F_i\right)$， $\gamma \left(B_1\right)\le \gamma \left(B_2\right)$。

证明：由距离的定义，对于任意 $B_1\subset B_2$，有

$d_{B_{\text{1}}}\left(x,y\right)={\displaystyle \underset{a\in B_{\text{1}}}{\sum }\left|a\left(x\right)-a\left(y\right)\right|}\le {\displaystyle \underset{a\in B_2}{\sum }\left|a\left(x\right)-a\left(y\right)\right|}=d_{B_2}\left(x,y\right)$

根据集合到集合间距离的定义有

$d_{B_1}\left(E_i,F_i\right)=\underset{x\in E_i,y\in F_i}{\min }{d}_{B_1}\left(x,y\right)\le d_{B_1}\left(x,y\right)$

$d_{B_{\text{2}}}\left(E_i,F_i\right)=\underset{x\in E_i,y\in F_i}{\min }{d}_{B_{\text{2}}}\left(x,y\right)\le d_{B_{\text{2}}}\left(x,y\right)$

因此

$d_{B_2}\left(E_i,F_i\right)-d_{B_{\text{1}}}\left(E_i-F_i\right)>0$

$d_{B_1}\left(E_i,F_i\right)<d_{B_2}\left(E_i,F_i\right)$

另外，根据定义1有

$\gamma \left(B_1\right)={\displaystyle \underset{i=1}{\overset{q}{\sum }}{d}_{B_1}}\left(E_i,F_i\right)$

$\gamma \left(B_2\right)={\displaystyle \underset{i=1}{\overset{q}{\sum }}{d}_{B_2}}\left(E_i,F_i\right)$

得到

${\displaystyle \underset{i=1}{\overset{q}{\sum }}{d}_{B_2}}\left(E_i,F_i\right)-{\displaystyle \underset{i=1}{\overset{q}{\sum }}{d}_{B_1}}\left(E_i,F_i\right)\ge 0$

因此

$\gamma \left(B_1\right)\le \gamma (\; B\; 2\; )$

引理得证。

从引理1看出，随着属性数目的增加，样本间距离函数值越大，依赖度函数值也越大。这意味着在属性子集中添加新属性从而提高了分类器的分类能力。现在，我们通过最大化依赖度函数给出属性约简的定义。

定义2：对于多标签数据 $S=\left(U,A,L\right)$，如果属性子集 $B\subseteq A$ 满足以下条件，则称集合B是A的依赖约简：

1) $\gamma \left(B\right)=\gamma \left(A\right)$ ；

2) 对于任意的 $B^{\prime }\subset B$，。

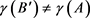我们可以看到约简的是A的一个极小子集，它保持了分类器的分类能力。然而，在现实应用中，上述定义过于严格，因此我们引入一个参数 $\epsilon$，并给出基于正负类边界距离的属性约简定义。

定义3：对于多标签数据 $S=\left(U,A,L\right)$，如果属性子集 $B\subseteq A$ 满足以下条件，则称集合B是A基于正负类边界距离的属性约简：

1) $\left|\gamma \left(B\right)-\gamma \left(A\right)\right|<\epsilon$ ；

2) 对于任意的 $B^{\prime }\subset B$， $\left|\gamma \left(B^{\prime }\right)-\gamma \left(A\right)\right|\ge \epsilon$。

在这里，我们通过引入参数 $\epsilon$ 来扩大属性约简的范围，并尽可能减少冗余属性，同时将正负类样本间距离的变化保持在较小的范围内。例1更详细地描述了约简过程。

例1：给出多标签数据集 $S=\left(U,A,L\right)$，如表1所示，样本集为 $U=\left\{x_1,x_2,x_3,x_4,x_5,x_6\right\}$，属性集为 $A=\left\{a,b,c\right\}$，标签集为 $L=\left\{l_1,l_2,l_3\right\}$。

Table 1. Multi-label data

表1. 多标签数据

正负类样本集如表2所示。

Table 2. Sample set

表2. 样本集

根据距离定义计算出正负类样本间距离，然后得到依赖度函数值，结果如表3所示。

Table 3. Distance

表3. 距离

根据定义3计算得到表4。

Table 4. Dependence degree

表4. 依赖度

根据定义3中的参数 $\epsilon =1$，则从表4中可看出属性集 $\left\{a,c\right\}$ 是正负类边界距离的属性约简。

现在，我们设计了一种基于正负类边界距离的属性约简算法。把定义3中的参数 $\epsilon$ 看作算法的停止条件，当依赖度的增加小于参数 $\epsilon$ 时，算法终止，完成属性约简。

变量 $A_k$ 是剩余的属性集，变量 $B_k$ 是选择的属性集。最初的剩余属性集就是全部的属性集A，从 $A_k$ 中任意选择一个 $a_j$，把它并到 $B_k$ 里，计算依赖度 $\gamma \left(B_k\cup \left\{a_j\right\}\right)$，有多少个属性就算多少个依赖度。然后选择依赖度最大的属性，在剩余属性 $A_k$ 里去掉，选择的属性 $B_k$ 中加上。选择最大的依赖度作为新的依赖度，当依赖增量小于参数 $\epsilon$ 时，算法终止，属性约简完成。当依赖增量大于参数 $\epsilon$ 时，回到第2步，选择了一个属性后还剩多少，然后循环上述过程，循环到满足不等式时，属性约简完成。在算法中， $\left|U\right|$ 是样本数， $\left|A\right|$ 是属性数，步骤2到步骤5是一个循环过程，循环 $\left|A\right|$ 次。因此，时间复杂度为 $O\left(\left|A\right|{\left|U\right|}^2\right)$。

4. 实验

为了评估PNBR算法的性能，本文在九个多标签数据集上实现了PNBR算法，并将实验结果与四种多标签属性约简算法进行了性能比较。这些算法包括PR、MDMR、FSSL和NLD，其中PR代表经典的正域约简算法 [12]、MDMR代表标签最大依赖和最小冗余算法 [13]、FSSL代表基于流标签的多标签学习的特征选择算法 [11]、NLD代表邻域标签依赖度约简算法 [14] 和PNBR代表我们提出的正负类边界距离的多标签数据属性约简算法。九个多标签数据集如表5所示。

Table 5. Multi-label data sets

表5. 多标签数据集

在我们的实验中，采用十折交叉验证来评估不同方法的有效性。十折交叉验证是将原始数据集随机分成10个大小相同的样本子集，轮流将其中9个子集当作多标签训练集，一个子集当作多标签测试集，进行实验。每次实验都会得出相应的正确率或差错率，10次实验结果的正确率或差错率的平均值作为对算法精度的估计。表6给出了实验后所选属性的平均数量，并用下划线突显了两个最佳结果。通过比较所选属性的平均数量可知，MDMR算法和PNBR算法更好，可以去除更多的冗余属性。而PR算法和FSSL算法相对差一点。

Table 6. Average numbers of the selected attributes

表6. 所选属性的平均数量

实验结果分析，对于数值型数据而言，PNBR算法和MDMR算法选择的属性最少。在Flags数据集中，它只保留了19个属性中的4或5个，这两种算法相对其他算法较差。然而在数据集Enron、Medical和Genbase中，随着数据属性数量的增加，属性减少的就不多了，这种影响就可以忽略不计了。

十折交叉验证的平均运行时间如表7所示，可以看出，MDMR算法、NLD算法和PNBR算法的运行时间比其他算法长，PR算法和FSSL算法的运行时间比其他算法短。

Table 7. Average running time

表7. 平均运行时间

实验结果分析，对于数值型数据而言，FSSL算法和NLD算法的计算时间大约是PR算法和MDMR算法的2倍，NLD算法和PNBR算法的计算时间大约是PR算法和MDMR算法的3倍。在Flags数据集中，由于数据集较小，所以算法的计算速度的差异不明显。

本文用分类器ML-9NN评估了五种属性约简算法的分类性能，同时，采用Hamming Loss、F₁ score和Coverage三种多标签分类的评价指标，来衡量约简数据的分类精度 [15]，其中下划线突显了两个最佳结果。

Table 8. Hamming loss

表8. 汉明损失

汉明损失反应的是错误分类的样本标签占总样本标签的比率，该指标取值越小，算法的性能越好，当值为0时达到最优。从表8可以看出，NLD算法和PNBR算法优于其他算法，MDMR算法和FSSL算法的性能略优于PR算法，结合表6和表7中的属性约简数量和运行时间，NLD算法和PNBR算法保留的属性更多，即使耗时长，但它的分类效果更好，特别是对于符号型数据。

Table 9. F1 score

表9. F₁分数

F₁ score相对于汉明损失是一个综合版本，F₁ score衡量分类的准确性，并忽略错误分类的样本。它是精确率和召回率的调和平均值，该指标取值越大，算法的性能越好，通常最大值为1，最小值为0，当值为1时达到最优。从表9可知，除数据集Core15k外，五种算法在F₁ score方面没有显著差异。对于Core15k数据集，NLD算法和MDMR算法的分类精度与原始数据差不多。

Table 10. Coverage

表10. 覆盖率

覆盖率表示算法生成的排序底部的真实标签的排序平均值。排序越大越不相关，所以这个覆盖率越小，算法性能越好。从表10看出，PR算法和PNBR算法优于其他算法。从数值上看，约简前后数据的分类精度并没有明显差异。实验结果表明所提约简算法能够建立合理的属性重要度排序，有效地去除冗余属性。

5. 总结

本文受基于集合到集合距离的启发，设计了一种基于正负类边界距离的属性约简算法，通过实验对所提的约简方法进行了评估，结果表明，所提约简算法能够建立合理的属性重要度排序，有效地去除冗余属性，并保持较高的分类精度。

实验研究表明，我们这个方法在处理大规模数据时，计算复杂度还是有点高，如何降低时间复杂度是我们今后要做的工作。另外在本文，我们将多标签数据分解中的标签看作为独立的，不相关的，但是在现实生活中，标签之间应该是有相关性的，所以，今后的研究工作中要将标签的相关性考虑进去，再做研究。