1. 引言
随着经济水平的快速发展,道路交通的需求量也随之增加,然而城市交通拥堵导致车辆行驶速度降低、行程时间延长、排放尾气增加、出行成本上升,这直接成为了制约城市发展的重要问题之一。因此,短时交通流预测研究对城市智能交通系统的建设发展具有重要意义 [1]。短时交通流预测是根据历史交通流数据对下一个时间间隔的交通流量进行预测的过程,既有缓解交通拥挤、提高运输效率的作用,也为城市交通规划提供了有效的依据。
从20世纪60年代开始,国内外学者就建立了多种模型用于短时交通流预测,主要可分为传统的数理统计模型、非线性理论模型以及人工智能模型。传统的交通流预测模型包括时间序列预测模型 [2] [3]、卡尔曼滤波模型 [4] [5]、自回归模型 [6]、傅里叶变换模型 [7] 等。随着人工智能的发展,更多的机器学习模型和深度学习模型开始运用于交通流预测。神经网络自学习能力强而且自适应性强,在识别复杂非线性问题中应用广泛,但存在算法收敛速度慢、预测精度低等缺点。支持向量机模型可以避免神经网络结构选择和局部极小点问题,在非线性、高维空间泛化性高,但对缺失数据敏感且仅局限于小集群样本。梯度提升树属于Boosting集成算法的一种,是一种迭代决策树算法,其由多棵决策树组成,每棵树都是对前序模型的不足之处进行改进,结果由各决策树累加而得到,从而得到了一个强学习器,但存在容易过拟合的问题。极端梯度提升算法(Extreme Gradient Boosting, XGBoost)在梯度提升算法的基础上做了进一步的改进,它在目标函数中加入了正则项并且采取列抽样,不仅防止模型过拟合,而且运算速度得到了明显的提升。
因此,为提高短期交通流预测精度及训练速度,本文采用XGBoost算法进行短期交通流预测。近年来,研究者采用多种调节参数方法对XGBoost算法进行优化,却较少优化XGBoost算法的目标函数。在本文中,为了充分发挥XGBoost算法的框架作用,根据交通流数据的特征,选用Huber损失作为目标函数。实验结果表明:基于Huber损失的极端梯度上升模型具有更高的预测精度,各误差指标小,且模型训练时间短,符合短时交通流预测所要求的时效性。
2. XGBoost原理
2.1. XGBoost目标函数定义
极端梯度提升算法(Extreme Gradient Boosting, XGBoost)是对梯度提升算法(Gradient Boosting Decision Tree, GBDT)的一种改进,通过在目标函数中添加正则项,进一步提升了算法性能。其定义如式(1)所示:
(1)
式(1)中,
为第t轮的预测值,其等于前
轮预测值加上新的函数
。在定义目标函数时,决策树自身存在惩罚项 [8]。惩罚项表达式如式(2)所示:
(2)
式(2)中:
为惩罚力度;
为参数;
为各叶子节点权重;T为叶子节点个数。因此,包含惩罚项的目标函数如式(3)所示:
(3)
用二阶泰勒展开式来近似原来的目标,泰勒展开式如式(4)所示:
(4)
根据式(4)的泰勒展开式以及式(3)的目标函数表达式,定义:
(5)
(6)
(7)
(8)
式中:
对应于泰勒展开式中的一阶导数;
对应于泰勒展开式中的二阶导数,故目标函数表达式可通过泰勒展开式转换为式(9):
(9)
将式(9)中的常数项移除后,得到目标函数的最终形式,如式(10)所示:
(10)
从式(10)可以看出,该目标函数的值仅取决于
和
。
2.2. XGBoost的目标函数求解
我们每次添加的树要使我们的目标函数最优,那么我们的目标函数可以写成:
(11)
上式中,
表示叶子节点一阶导,
表示叶子节点二阶导。从上式可以看出XGBoost
较于其他算法的优越性之一就表现在将样本遍历转化为叶子节点遍历,这样提高了运算速度。
最后的目标函数是关于
的二次函数,这样它的极小值点和极小值分别为:
(12)
(13)
最后一个式子正是衡量树结构好坏的标准,
值越小代表结构越好。当我们指定损失函数后,就可以求出
和
,继而可以得到目标函数的极小值。通常,我们选用的损失函数为均方误差(Mean Squared Error, MSE)或者平均绝对误差(Mean Absolute Error, MAE)。
有了这个标准后,我们理应尝试所有可能并选择最优,然而太费时。于是我们每次优化树的一层。我们假设一个叶子分裂为两个叶子,则它的得分增加为:
(14)
如果增益小于
,我们就不将此叶子分裂。
3. 基于XGBoost算法的交通流预测模型
3.1. 自定义XGBoost目标函数
机器学习中的所有算法都依赖于最小化或最大化某一个函数,我们称之为“目标函数”,最小化的这组函数被称为“损失函数”。在建立模型时,为了充分发挥XGBoost算法的框架作用,需要根据不同的数据集以及任务自定义目标函数,来达到更优的效果 [9]。
均方误差(Mean Square Error, MSE)是目标变量与预测值之间距离的平方和,平均绝对误差(Mean Absolute Error, MAE)是目标变量和预测值之间距离的绝对值之和。以MSE为损失函数的模型会给离群点赋予更高的权重,而以MAE为损失函数的模型对于小的损失值,其梯度也很大,而且其导数并不连续,求解效率较低。Huber损失结合了MSE与MAE的优点,降低了对离群点的惩罚程度,能增强MSE对离群点的鲁棒性。
在本文中,根据交通流数据的特征,选用Huber损失作为目标函数。Huber损失的定义如下:
(15)
式中:
表示真实值;
表示预测值;
是一个常数,表示邻域,可以通过调节参数得到
的最优取值。
Huber损失是不可导函数,所以在本文中用的是Huber损失的可导逼近形式(伪Huber损失函数作为目标函数),其定义如下:
(16)
式中:
,表示预测值与真实值的误差。
伪Huber损失函数的一阶导数为:
(17)
伪Huber损失函数的二阶导数为:
(18)
当预测误差小于
时,Huber损失函数采用平方误差;当预测误差大于
时,Huber损失函数采用的是线性误差。
3.2. 交通流预测模型实现流程
基于交通流数据在时间上的变化规律,采用上述模型对交通流数据实现实时预测。实现流程可分为4个阶段:数据处理阶段,特征提取阶段,模型优化阶段,可行性分析阶段 [10]。具体流程如图1所示。
数据处理阶段:对采集数据进行缺失值填充等预处理,处理后将数据集分为训练集与测试集。
特征提取阶段:对数据集的规律进行刻画描述,提取时间特征,并对各个特征进行重要性分析,选取重要性程度最高的6个特征。
模型优化阶段:对XGBoost模型的目标函数进行优化,并且采用Hyperopt方法对各个参数进行调节。
可行性分析阶段:利用训练好的模型在测试集上进行测试,将预测结果与真实值进行比较,获取模型预测性能。将本文模型与常用预测模型进行比较,分析模型可行性。
4. 实例分析
4.1. 数据来源
本文所用交通流数据来源于美国加利福尼亚州戴维斯附近的I80走廊,传感器设置如图2所示。数据采集时间为2016年1月1日至10月12日,采集时间间隔为所30 s。该数据集共包含812,792组数据。为构建基于XGBoost算法的短期交通流预测模型,本文采用7、8月份的数据来进行建模分析。具体的,用24天的数据(7月1日~7月24日)作为训练集,用10天(7月25日~8月3日)的数据作为测试集。

Figure 1. Realization process of traffic flow prediction model
图1. 交通流预测模型实现流程

Figure 2. Sensor settings in I80 Corridor, California
图2. 加利福尼亚州I80走廊传感器设置
4.2. 数据预处理
数据集中存在不规则小数据量间断性缺失情况。因此,需要对数据进行插补修复。考虑到交通数据的动态特征和即时特性,实验过程中使用历史均值法和最近邻均值法(取该缺失数据上下时间节点的平均值作为插补值)相结合的方法进行填充。历史均值法适合连续缺失数据,最近邻均值法适合单点缺失数据。
通过修复得到完整数据,之后继续将交通流处理成以5 min为间隔的数据,便于进一步分析、训练和预测。
在得到完整的数据集后,将对交通流数据的分布进行刻画。随机选取某一周数据(2016年7月11日~2016年7月17日)和某一天数据(2016年7月11日)进行考察,分别如图3、图4所示。横坐标表示交通流量,纵坐标表示密度。可以发现,其分布很符合二维的混合高斯分布。高斯分布具有很好的数学性质,因此不需要进行数据变换。
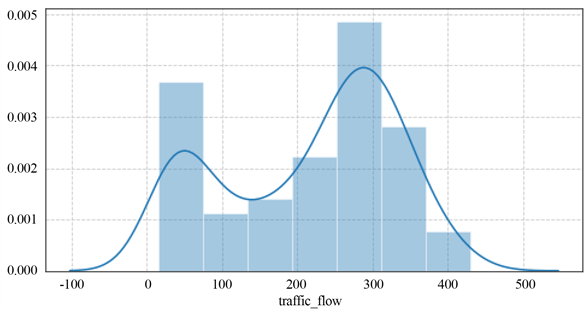
Figure 3. One-day traffic flow data distribution map
图3. 一天交通流数据分布图
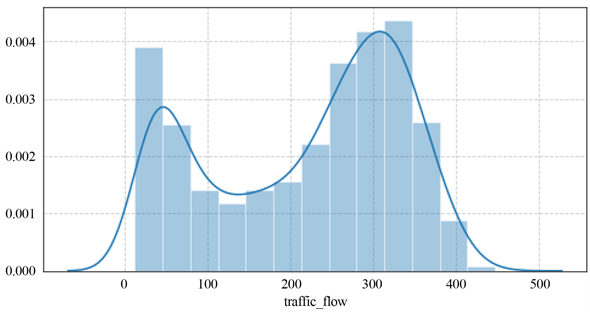
Figure 4. One-week traffic flow data distribution map
图4. 一周交通流数据分布图
4.3. 特征提取
首先对交通数据规律进行描绘观察,随机选取连续两周(2016年7月1日~2016年7月14日)的交通数据进行刻画,通过观察处理后的数据(时间间隔为5 min)容易发现,交通流数据具有极强的周期性及连续性,即时间相近的数据其状态也更相似,如图5所示(横坐标表示时间组数,每组时间为5 min;纵坐标表示交通流量)。

Figure 5. Two-week traffic flow data graph
图5. 两周交通流数据图
实验中,提取交通流数据的月周期特征、周周期特征、最近前3天状态特征、最近前2天状态特征、最近前1天状态特征和最近5 min的状态特征,共6个特征作为数据属性,整理数据集用以训练和预测。
对模型各个特征进行重要性分析,如图6所示(f0表示月周期特征,f1表示周周期特征,f2表示最近前三天状态特征,f3表示最近前两天状态特征,f4表示最近前一天状态特征,f5表示最近5 min的状态特征)。

Figure 6. Feature importance analysis chart
图6. 特征重要性分析图
由图6可知,最近5 min的状态特征最重要,因为交通流数据是时间序列数据,下一时刻的状态必定与上一时刻的状态紧密相关;周周期特征重要性排名第二,是否是工作日对交通流预测具有很重要的影响;重要性排名第三的特征是最近前1天状态特征,排名第四的是月周期特征,排名第五的是最近前2天状态特征,排名最后的是最近前3天状态特征。
4.4. XGBoost参数调优
XGBoost模型参数众多,使用Hyperopt方法对各个参数进行调节,如表1所示。

Table 1. Parameter value of traffic flow prediction model
表1. 交通流预测模型参数取值
1) n_estimators:弱学习器的最大迭代次数,或者说最大的弱学习器个数。n_estimators太小,容易欠拟合,n_estimators太大,又容易过拟合。
2) learning_rate:学习率,可以减少每一步的权重,提高模型的鲁棒性。
3) max_depth:数的最大深度。
4) min_child_weight:决定最小叶子节点样本权重和。
5) scale_pos_weight:样本十分不平衡时,将这个参数设置成正数,可以使算法更快收敛。
6) subsample:随机采样比例。
7) colsample_bytree:列采样率,也就是特征采样率。
8) gamma:分裂节点时,损失函数减小值只有大于等于gamma,节点才分裂。
4.5. 模型预测结果及分析
为评估模型的效果,对未来10天(7月25日~8月3日)的交通流进行预测,如图7所示。

Figure 7. Ten-day prediction graph
图7. 基于Huber损失的XGBoost模型十天的预测图
图7中蓝色曲线为7月25日~8月3日实际的交通流数值,红色曲线表示由该模型进行预测的交通流预测值。从图中可以看出,红色曲线和蓝色曲线是基本重合的,这表示本文中提出的XGBoost模型能够很好地拟合交通流数据,且预测精度非常高。为了更清晰地展示该模型的效果,可选择从10天预测数据中随机抽取某一天来进行展示,如图8所示。图8中蓝色曲线为随机抽取的7月25日的交通流实际值,红色曲线为模型预测值。
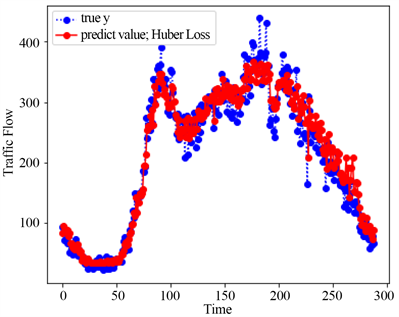
Figure 8. Single-day prediction graph
图8. 基于Huber损失的XGBoost模型的单天预测图
5. 不同模型预测结果对比分析
5.1. 不同模型预测结果评价指标
使用3种常用的性能指标来对模型的预测效果进行判定,它们分别是均方根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和决定系数(R2),从不同侧面来反应模型的预测效果。各指标定义如下:
(19)
(20)
(21)
式中,
为真实值,
为预测值,
为均值,m为测试样本个数。
通过计算上述3个性能评价指数值,来评估所建模型的预测性能。均方根误差和平均绝对误差越小模型效果越好,R2越接近于1,模型越好,反之,越差。
5.2. 不同模型预测结果对比
为评价基于不同自定义目标函数的XGBoost模型的预测性能,同时采用Huber损失、均方误差以及平均绝对误差作为XGBoost模型的目标函数对7月26日的交通流进行预测,并将预测结果与真实值进行比较,如图9所示。
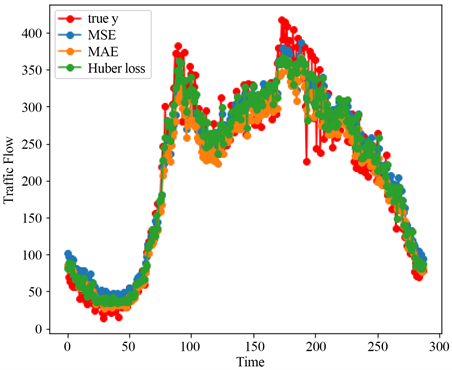
Figure 9. Comparison of different objective functions
图9. 基于不同目标函数的XGBoost模型结果对比图
图9中红色曲线为7月26日实际的交通流数值,蓝色曲线表示基于均方误差的XGBoost模型的预测值,橙色曲线表示基于平均绝对误差的XGBoost模型的预测值,绿色曲线表示基于Huber损失的XGBoost模型的预测值。从图中可以看出,绿色曲线和红色曲线的重合度最高,这表示本文提出的基于Huber损失的XGBoost模型能够很好地拟合交通流数据,且预测精度非常高。
为直观获取各模型预测精度的差异,采用5.1节提出的性能评价指标对各模型预测结果进行评价,如表2所示。

Table 2. Comparison of different objective functions
表2. 基于不同目标函数的XGBoost模型结果对比
由表2可知,将Huber损失作为目标函数的XGBoost模型所得到的均方根误差、绝对平均误差以及R2均优于将均方误差损失作为目标函数的XGBoost模型与将平均绝对误差损失作为目标函数的XGBoost模型。将Huber损失作为目标函数的XGBoost模型误差最小,预测精度最高,预测效果是最佳的。
为评价基于Huber损失的XGBoost模型的预测性能,同时采用支持向量回归模型、梯度提升回归模型进行预测,并将预测结果与基于Huber损失的XGBoost模型的预测结果及真实值进行比较,如图10所示。
图10中蓝色曲线为7月26日实际的交通流数值,红色曲线表示基于Huber损失的XGBoost模型的预测值,橙色曲线表示梯度提升回归模型的预测值,绿色曲线表示支持向量回归模型的预测值。从图中可以看出,红色曲线和蓝色曲线的重合度最高,这表示本文提出的基于Huber损失的XGBoost模型能够更好地拟合交通流数据。
为直观获取各模型预测精度的差异,采用5.1节提出的性能评价指标对各模型预测结果进行评价,如表3所示。

Table 3. Comparison of different model results
表3. 不同模型结果对比
由表3可知,基于Huber损失的XGBoost模型所得到的均方根误差、绝对平均误差以及R2均优于梯度提升回归模型和支持向量机回归模型,其误差最小,预测精度最高,预测效果是最佳的。因此,本文中提出的基于Huber的XGBoost模型能够从数据本身的特性出发,来对数据进行深层的探索,模型的建立也更加科学合理。
6. 结语
本文建立了一种基于Huber损失的极端梯度上升(Extreme Gradient Boosting, XGBoost)短时交通流预测模型,实验表明该模型优于基于均方误差损失的极端梯度上升模型以及基于平均绝对误差损失的极端梯度上升模型。同时,该模型较梯度提升回归模型、支持向量机回归模型具有更高的预测精度,各误差指标小,且模型训练时间短,符合短时交通流预测所要求的时效性,具有一定应用价值。需要指出的是,本文未考虑交通流的空间特性,下一阶段仍需研究多因素影响下的交通流预测,进一步加强模型鲁棒性,使其适用于复杂情形下的交通流预测。