1. 引言
在实际工程应用中对于不确定性结构设计和评价安全性能等方面,采取可靠度分析能获得较好的效果。由国际安全度联合委员会一致推荐的一次二阶矩方法能够在对常规问题进行可靠度分析时起到较好的应用效果。其实质是泰勒级数展开功能函数只对一次项保留,对随机变量的前两阶段作近似计算,以此实现对相应可靠度指标的有效获取。在极限状态曲面中具有几何意义的可靠性指标称为最可能失效点(MPP)或验算点,验算点的搜寻在迭代计算中是一个难点。FORM中的验算点法(HL-RF)以其计算精度较高、耗时少等优点而在求解结构可靠度指标方面得到广泛应用。当功能函数相对应的非线性程度处于较低水平时,通过对这种方式的应用能够使得最终所得到的结果在准确度方面得到更有力的保障;不过当功能函数相对应的非线性程度处于偏高水平,同时还存在二维以及二维以上的多维变量时,迭代阶段之中的HL-RF普遍都会存在震荡、混沌甚至不收敛。
为了解决HL-RF对高维非线性功能函数收敛困难的问题,多名学者提出了很多优化迭代算法。Yang [1] 等人利用混沌理论探讨了可靠性指数在FORM中产生周期和混沌解的根本原因,指出FORM的非收敛性不依赖于极限状态函数的大曲率和非线性程度。基于混沌控制原理,Yang、Yi、Yang、Li [2] [3] 分别采用稳定性变换方法(STM)控制非线性地震分析性能测量方法和容量谱方法的迭代失效。Li [4] 等人提到了提高非线性规划算法鲁棒性的方法,同时给出了FORM算法的优化版本。Gong [5] 等人对迭代步长做出适当的调整,从而完成了对FORM算法相应迭代阶段当中收敛性的有效改进。杨迪雄 [6] 采取的混沌反馈控制方法主要是稳定转换,对FORM迭代算法中的混沌控制、分岔和诊断等问题进行解决,但是操作复杂且收敛速度较慢。李彬 [7] 等的自适应稳定转换法是在Armijo准则基础上提出,其混沌控制因子是基于Armijo准则自行调整变换。在上述求解方法中未能从FORM中迭代算法的本质上理解功能函数不收敛的原因。
本篇文章以混沌动力学的相关知识为基础,完成了能够使得计算精度以及计算效率都得到有力保障的混沌控制算法。通过对混沌控制算法当中全局收敛性显著的稳定转化法的合理应用,实现对HL-RF方法的有效控制。除此之外,通过对函数震荡判据的适当引入来实现对迭代阶段中振荡问题的有效解决。凭借着对许多例子具体结果的适当引入,可以确保这种算法的收敛性以及计算效率都处于偏高水平,同时算法的鲁棒性以及有效性也能够得到有效验证。
2. 可靠度指标的定义
1969 年Cornell提出结构可靠度的衡量可采取结构的标准差和均值,凭此完成一次二阶矩方法的合理构建。从可靠度指标的角度出发,Hasofer和Lind对其概念进行重新定义,使其处于不同的功能函数下,确保可靠度指标是唯一的,从而对可靠性相关理论作出有效的完善。从几何意义的角度出发,可靠性指标也能够被定义为非线性等式约束优化模型的解:
(1)
在上面所给出的式子当中,
以及
所代表的分别是标准状态空间条件下的随机控制变量以及功能需求函数或者极限状态函数。
表示的是可靠度指标。优化模型的最优解已经代表着可能性最高的失效点或者验算点。从几何的角度出发,可靠度指标的问题会被定义成标准正态空间当中,所设定的坐标原点和相对应的极限工作状态空间曲面之间距离的最小值。从非正态分布随机变量的角度出发,能够选择通过Rosenblatt变换或者JC法来实现原本的非正态分布随机变量向标准正态随机变量的有效转化。之后再完成可靠度指标的有效求解。
3. 基于混沌控制的HL-RF迭代算法
HL-RF迭代算法在应用过程当中的首要步骤就是完成初始迭代点
的合理确定,紧接着以点迭代公式为基本完成对下一次迭代的有效求解,这个求解的过程会持续到相对应的收敛条件已经得到完全满足。这个算法会将相对应的功能函数放置在第k个迭代点
上,同时通过一级泰勒级数进行展开。除此之外还会要求第
个迭代点
上的功能需求函数能够满足
,可得:
(2)
令
到原点的距离为
,结合 的负梯度方向,则有:
的负梯度方向,则有:
(3)
结合式(3),可以得到:
(4)
 (a) 收敛
(a) 收敛 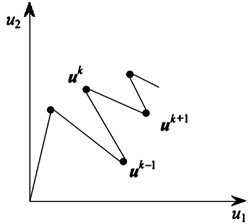 (b) 振荡收敛
(b) 振荡收敛  (c) 不收敛
(c) 不收敛
Figure 1. Three typical iteration histories
图1. 三种典型的迭代历史
图1给出了以下三种经典的迭代发展过程。如图1所示,迭代学习阶段当中的随机变量会呈现出逐渐收敛的趋势到相应的验算点,这个条件下的功能函数所表现出的非线性影响程度较低,如果是较高的非线性,极易出现随机变量迂回震荡的现象,此时计算工作效率水平较低,甚至会导致分析结果不收敛。因此,利用混沌反馈控制算法中的稳定性转换方法收敛控制HL-RF迭代算法。通过稳定转换法可以把HL-RF迭代的式(4)转化为下列表达式:
(5)
其中,Yang [1] 等从混沌动力学出发对一次二阶矩法数值不稳定性机理进行分析,基于混沌控制理论的稳定转换法提出了改善一次二阶矩收敛性的混沌控制算法(CC),
表示下一个迭代点的方向向量,可以通过CC算法求得;
为混为沌控制因子,取值范围是
;
是一个n维对合矩阵,一般取单位矩阵
。
如图1(a)中所示,对于通过减小每个迭代步骤的迭代过程的混沌控制方法,相对应的迭代点会呈现出逐渐收敛的趋势到相应的验算点。通过对图1(b)以及图1(c)的观察能够明显得到导致损失函数收敛速度较低或者完全不收敛的基本原因,就是极限工作状态曲面当中相应点的负梯度具体发展方向出现震荡。
因此选择通过某种判定准则的引入来对迭代阶段当中是否存在震荡情况做出有效判断。
(6)
其中
可以表示标准正态空间中第k步迭代的随机变量,
代表一个功能函数g对随机变量负导数研究方向的单位方向向量。当
时,表示两个向量之间的夹角小于90˚,则迭代点没有发生震荡;反之,如果
,表示两个向量之间的夹角大于90˚,则迭代点发生了震荡。如果函数迭代过程中没有震荡,可以采用经典的HL-RF迭代运算,直到收敛为止,否则收敛强的算法应该更好。
通常情况下混沌的控制因子都是0.1以及0.5,不过实际情况当中,应根据非线性程度来选择控制因子。非线性度越高,控制因子越小,反之亦然。基于混沌控制在迭代过程中的实际作用,即使当前迭代点更准确有效寻找到下一迭代点,根据
和
两点与极限状态曲面的负梯度方向的夹角
和
,按照以下模型来确定混沌控制因子
,即
(7)
其中q为松弛因子,通过调节
来确定
。一般情况下可取
。
综合上面公式,算法的迭代步骤如下:
1) 通过变换,实现随机变量
到相对应的标准正态随机变量
的合理变换。
2) 令
,选择随机变量的均值
作为初始变量。
3) 由式(6)判定迭代过程中是否发生震荡,如果
,迭代过程中无震荡,则使用式(4)和式(3)分别计算可靠度指标
和下一步迭代点
;如果
,则迭代过程中出现震荡,此时转入式(5)和式(4)计算可靠度指标
和下一步迭代点
。
4) 完成标准正态空间当中随机变量
到相对应原空间
的有效转变。
5) 对迭代点前后两次间所存在的误差进行计算
,
代表着所规定范围之内的允许误差。假设已经满足条件,就可以停止迭代,不满足条件就会返回到步骤2)并反复进行。
4. 计算实例
实例1:对于二维随机变量的结构功能函数,可通过下式来描述其极限状态:
当中x1及x2全部服从标准正态分布随机变量并且相互独立。所设定的允许误差
。
分别采用经典HL-RF方法、CC算法以及本文方法求解,松弛因子取2。CC算法采用固定的混沌控制因子(此题中混沌控制因子取0.5),其迭代式基本与本文一致,因此可作为算例对比方法。表1以及图2所列举出的就是三种方式所分别得出的计算结果以及相应的迭代历史。通过对图2的观察,可以发现选择HL-RF方法会无法收敛到相应的验算点。而CC方法就能够对迭代阶段中存在的震荡现象做到有效避免。不过会造成比较多的迭代次数以及比较慢的收敛速度。本文所提出的方法能够在对随机变量震荡做到有效控制的前提条件下,对整体的计算效率做到有效提高。

Table 1. Calculation results of two-dimensional examples
表1. 二维实例计算结果
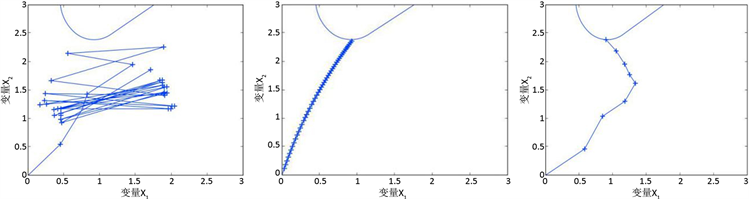 (a) HL-RF方法(b) CC方法(c) 本文方法
(a) HL-RF方法(b) CC方法(c) 本文方法
Figure 2. Iterative history of two-dimensional instances
图2. 二维实例的迭代历史
实例2:多维高非线性结构功能函数。考虑某一含高频噪声项的功能函数为:
允许误差
,相应的初始迭代点也就代表着随机变量均值。因为功能函数属于多维高非线性,故取0.03为CC混沌控制因子。表2所示的就是三种方式所分别得出的最终计算结果。HL-RF迭代计算结果无法收敛,CC方法具体的收敛速度过慢。本文方法能够在保证找到验算点的前提条件下,对整体的收敛速度做到有效提高。

Table 2. Calculation results of high-dimensional examples
表2. 高维实例计算结果
5. 结论
如果功能函数非线性程度较高,在结构可靠指标迭代计算时HL-RF算法会出现混沌、震荡甚至不收敛的现象。本文基于这种迭代过程中不稳定的认识,以HL-RF算法为基础完成稳定转换法的合理引入,同时凭此完成有效的收敛控制,并利用混沌控制因子与迭代过程出现混沌的原因,建立关系等式使每步迭代更加高效收敛。在此基础上引入了一种新的函数进行判定纠正,该函数可以根据迭代点之间的夹角来判段迭代计算中是否产生了震荡。本文算法的实际效果在实例中已呈现,不仅验证了基于混沌控制算法的稳定性,也保证了该算法有更高的可靠性。
致谢
本次论文的整个完成过程都离不开罗文强老师的悉心指导,在完成论文的过程当中我体会到了来自老师的悉心指导以及无私奉献,为了使得本篇论文能够高质量的完成,老师甚至从自己的休息时间当中抽出时间对我进行指导,这种敬业精神和对学生的关怀精神使我深受感动,因此在这里对老师献上最为诚挚的谢意。
基金项目
国家重点基础研究发展计划“973”计划(No.2011CB710605)和国家自然科学基金项目(No.41972289)资助。