1. 引言
ZK方程是研究地球物理流动中旋涡的一个非常有吸引力的模型方程,ZK方程出现在物理、应用数学和工程的许多领域。特别是作为描述由冷离子和热等温电子组成的强磁化无损等离子体中非线性离子声波的重要模型,(3 + 1)维Zakharov-Kuznetsov方程的行波问题受到广泛关注。
2010年,利用经典向量场方法和相关向量场方法,Dong等人导出了(3 + 1)维Zakharov-Kuznetsov方程的约化和一些新的解 [1]。2012年,Zhang和Zhou [2] 利用分岔理论得到了一般形式的ZK方程的有界孤立波解、周期解、扭结解和反扭结解。2013年,Wronskian利用形式展开法获得了(3 + 1)维Zakharov-Kuznetsov方程的新的相互作用解 [3]。随后,S. Sahoo和S. Saha-Ray利用改进的分式子方程方法,构造了(3 + 1)维广义分式KdV-Zakharov-Kuznetsov方程的解析精确解 [4]。2016年,Moleleki等人提出用Kudryashov和Jacobi椭圆函数方法构造(3 + 1)维Zakharov-Kuznetsov方程的精确解 [5]。2017年,Lu等人利用改进的扩展直接代数方法得到了(3 + 1)维非线性扩展Zakharov-Kuznetsov方程和修正的KdV-Zakharov-Kuznetsov方程的新的精确孤波解、孤子解和椭圆函数解 [6]。同年,利用Kudryashov方法的修正形式,得到了共形时间分数维(3 + 1)维方程的精确解 [7]。2018年,Wang等人利用改进的扩展映射方法,得到了不同形式的精确行波解,如亮孤子、周期孤波、暗孤子等 [8]。2019年,利用(G'/G,1/G)展开法得到了(3 + 1)维Zakharov-Kuznetsov方程的三角函数解、双曲函数解和有理函数解。近年来,利用统一方法得到了孤立波解、孤子波解、椭圆波解和周期(双曲)波有理解 [10]。
虽然关于(3 + 1)维Zakharov-Kuznetsov方程的行波解已有许多深入的研究成果,但仍存在一些有待解决的问题。首先,我们注意到(3 + 1)维Zakharov-Kuznetsov方程的行波没有被讨论完全,特别是其无界行波。此外,虽然上述重要方法可以用来求(3 + 1)维Zakharov-Kuznetsov方程的行波解,但仍有一些行波解丢失。这些问题再次引起我们对(3 + 1)维Zakharov-Kuznetsov方程行波的研究兴趣。
本文考虑具有幂律非线性的(3 + 1)维Zakharov-Kuznetsov方程:
(1)
在这里
是实数,我们的目的是用动力系统的分岔方法研究当n = 1时方程(1)的所有行波解,并给出所有行波解(包括有界和无界)的显式表达式。论文的其余部分安排如下。第二节详细研究了方程(1)行波系统的相空间几何,得到了各种有界和无界轨道的参数分岔集。第三节利用第二节的结果,对方程(1)行波系统的所有轨道进行了分类。最后,通过对复杂椭圆积分的计算,给出了方程(1)所有行波解的精确表达式,包括有界和无界。第四部分是本文的结论。
2. 使用行波系统及其分岔分析
做以下行波变换
我们将方程(1.7)转换成相应的行波系统,如下所示:
(2)
这里
表示
,
表示波数。对方程(2)积分并且保留一个积分常数,我们可以得到:
(3)
e是一个积分常数。方程(3)有以下等价形式:
(4)
系统(4)是一个哈密顿系统,其能量函数为:
(5)
当n = 1时,系统(4)转换成以下形式:
(6)
首先,我们讨论系统(6)的平衡点个数及类型。
定理2.1:当
,系统(6)有两个平衡点,如果
,一个鞍点
和一个中心
;如果
,一个中心
和鞍点
。当
,系统(6)有一个独特的尖点
。当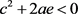 ,系统(6)没有平衡点。
,系统(6)没有平衡点。
证明:当
,通过直接计算,系统(6)有两个平衡点
,
。用
表示系统(6)的在平衡点
的雅可比矩阵,可以得到:
其行列式为:
通过哈密顿系统的性质,可以得到
是一个鞍点并且
是一个中心。类似的证明可以得到b < 0的情况。
当
,系统有一个平衡点
,其幂零矩阵为:
这意味着
是一个退化的平衡点。为了进一步讨论
的类型,我们做以下同胚变换:
把系统(6)转化成以下标准形式:
通过微分方程定性理论 [11],可以得到
,
,这证明了
是一个尖点。
当
,很容易得到系统没有平衡点。证毕。
接下来我们需要讨论分岔参数集
,
和
。基于平衡点的分析以及哈密顿系统的性质,我们有以下结果:
Case 1:对于
,这里有一个同宿轨
连接着鞍点
。在同宿环
内部,存在一系列周期轨
,这些轨道围绕着中心:
此外,当
,
趋近于
;当
,
趋近于
。在同宿环
之外的,所有轨道都是无界轨道,如图1(a)。
Case 2:对于
,系统(6)的所有的轨道都是无界的。这里存在两个特殊的轨道
和
,
的
极限集和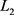 的
极限集对应于相同的平衡点
,如图1(b)。
的
极限集对应于相同的平衡点
,如图1(b)。
Case 3:对于
,系统(6)仅有一种类型的轨道。所有的轨道都是无界的,如图1(c)。
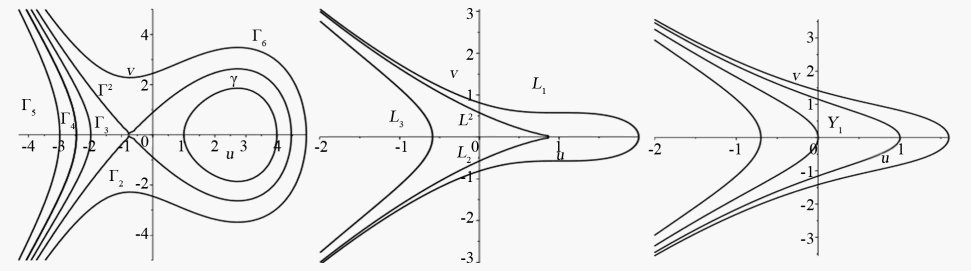 (a) a = 1, c = 1, e = 1 (b) a = 1, c = 1,
(c) a = 1, c = 1, e = −1
(a) a = 1, c = 1, e = 1 (b) a = 1, c = 1,
(c) a = 1, c = 1, e = −1
Figure 1. The phase portraits of (6)
图1. 系统6的相图
3. 方程(1)的精确解
在这一节中,我们寻求方程(1)所有行波解的精确表达式。它需要我们根据不同参数分岔集中能量函数的不同水平曲线来识别系统(6)的各种轨道,包括有界轨道和无界轨道。
3.1. 系统(6)的有界行波解
通过定理2.1,只有当
,才会存在有界行波,分别是周期波和孤立波,实际上,这些有界行波解已经在我们的前期工作中得到了 [12],但为了本文的完整性,我们给出其计算结果。
周期轨:
同宿轨:
3.2. 系统(6)的无界行波解
除同宿轨道和周期轨道外,系统(2.5)的所有轨道都是无界的。我们需要分三种情况讨论。
1) 首先,我们讨论
的情况。这里包含了5种情况(U1~U5)。
U1:考虑图1(a)中的第一种无界轨道
和
,其能量等于鞍点
。它们可以分别表示为:
这里
和
并且
。首先,我们用
作为例子来计算相应的解。给一个初始值
,有:
注意到,
我们得到第一种类型的无界解:
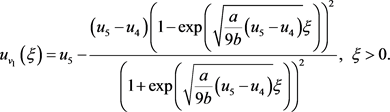
对于轨道
,采用类似的计算可以求出相应的无界解,其形式与
相同。
U2:考虑图1(a)中的第二种无界轨道,以
为例,其能量低于鞍点
,但高于中心
。任意一个轨道可以表示为:
这里
。选择一个初始值
,有:
通过计算,
这里
,
,我们得到第二种类型的无界解:
U3:考虑图1(a)中的第三种无界轨道,以
为例,其能量等于中心
。其轨道可以被表示为:
这里
,
并且
。类似的选择
上面的轨道,给定初值
,有以下精确表达式:
注意到:
我们得到第三种类型的无界轨道:
U4:考虑图1(a)中的第四种无界轨道,以
为例,其能量低于中心
。任一轨道可以被表示为
在这里
。令
,有
通过计算:
这里
,
以及
。我们可以得到第四种类型的解:
U5:考虑图1(a)中的第五种无界轨道,以
为例,其能量高于中心
。任一轨道可以被表示为
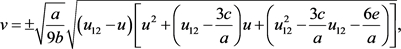
在这里 ,
。令
,有
,
。令
,有
类似的计算如U4,可以得到第五种类型的无界解:
2) 接下来,我们讨论
的情况。这里包含了2种情况(U6~U7)。
U6:考虑图1(b)中的第一种无界轨道
和
,其能量等于尖点
。它们可以分别表示为:
这里
。选择
,有
直接计算,可以得到第六种无界解:
U7:考虑图1(b)中的第一种无界轨道
或
,其能量等于尖点
。任意一个轨道可被表示为:
在这里
同时
。给定初值
,直接计算可以得到第七种无界轨道:
3) 最后,我们讨论
的情况。这种情况下,只有一种类型的无界轨道。任意一个都可以被表示为:
在这里
。给定初值
,有
因此,我们得到了最后一个无界解:
4. 结论
本文应用动力系统分岔法延伸了以前的工作同时研究了当n = 1时,(3 + 1)维Zakharov-Kuznetsov方程的所有类型的单波解。我们的结果展示了n = 1时的所有的ZK方程行波解可以被划分为10种类型,包括周期波解、孤波解和8种类型的无界行波解。它们的精确表达式完全可以用各种椭圆函数来计算。