1. 引言
反转性起源于物理学,最终与复分析、逼近论、数论、算子理论相结合。W. Jarczyk在文献 [1] [2] 中最早研究了函数方程的反转性。他证明了一个开区间上的连续反转自映射是两个连续对合函数的复合。设A是拓扑空间X中的非空闭集,
表示
的n次迭代,其中
,
。1815年,C. Babbage给出了迭代根问题 [3]
其中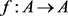 是给定的函数。作为迭代根问题的自然推广,多项式型迭代方程
是给定的函数。作为迭代根问题的自然推广,多项式型迭代方程
引起了学者的兴趣。对于线性F,即
(1.1)
1974年,S. Nabeya [4] 研究了n = 2的情况,即二阶迭代方程。2010年,张文萌与张伟年 [5] (引理3)揭示了方程(1.1)的
解与对应的齐次方程
(1.2)
的
解是平移关系。将
代入(1.2),得到特征方程
(1.3)
称r为特征根。在一定条件下,许多文献利用线性解
表达了方程(1.2)全部的
解(见 [6] - [12])。然而到目前为止,当n = 3时,方程(1.2)的
解也没有完整的结果。
借助文献 [12] 的
解结果,本文研究三阶多项式迭代方程的反转解存在性及其构造。在一定条件下,我们给出了齐次方程
(1.4)
和非齐次方程
(1.5)
的反转解,其中
,
。
2. 预备知识
如果一个同胚
等于它的逆,即
,称同胚
是对合的。一个同胚f是反转的,如果f通过一个对合共轭于它的逆
,即
令F是拓扑空间X中的非空闭集,
是一个递减的对合函数。
中的两个元素称为
-对称,如果
把一个元素的左端点映到另一个元素的右端点。
定义2.1 [1] 若同胚
无不动点,或者存在一个递减的对合函数
使得
-对称函数
的图像位于对角线的一侧,称f是对称的。
引理2.1 (引理1, [5]) 若
是方程(1.2)的
解,则f是一个同胚。
引理2.2 (引理2.4, [12]) 若方程(1.2)的
解
有一个非零不动点,则(1.3)至少有一个特征根等于1。
引理2.3 (注4, [2]) 一个递减的同胚是连续反转的充要条件为它是一个对合。
引理2.4 (定理1, [1]) 开区间上的一个递增同胚是连续反转的充要条件为它是对称的。
引理2.5 方程(1.4)的
解
是对合函数当且仅当
或
。
证明 显然,若 或
,f是对合的。反之,我们证明:若方程(1.4)的
解
是对合的,有
,
。一方面,由引理2.1,我们说
解f是一个同胚。根据方程(1.4),有
或
,f是对合的。反之,我们证明:若方程(1.4)的
解
是对合的,有
,
。一方面,由引理2.1,我们说
解f是一个同胚。根据方程(1.4),有
即
(2.1)
说明f是一个线性函数。
另一方面,方程(1.4)的所有线性解为
不失一般性,将线性解
代入方程(2.1),得到
也就是
若
,有
,即
或者
,说明
或 。若
,注意到
,我们得到
,
。故
,即
或
。
。若
,注意到
,我们得到
,
。故
,即
或
。
3. 特征根同号
在这一节,我们研究方程(1.4)在特征根同号情况下的反转解。
引理3.1 (定理1, [13];定理1, [12]) 设
(或
)。若
是方程
(3.1)
的
解,则
,并且f严格递增,满足双边Lipschitz条件
(3.2)
引理3.2 (定理3.1, [12]) 设
,则方程(1.4)的所有
解
严格递增,并且
i) 若f有不动点,则0是唯一不动点,且满足
(3.3)
其中
是下面二阶迭代方程的
解
ii) 若f无不动点,则
或
,
,可以用分段定义构造。
定理3.1 设
,则方程(1.4)除
和
之外的所有
解
都是反转解。
证明 在条件
下,根据引理2.2,方程(1.4)有两类解:
i) 若
解f有不动点0,根据引理3.2,有
(3.4)
(3.5)
或者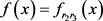 ,其中
。
,其中
。
根据不等式(3.2),(3.4)和(3.5)是对称函数,
和
不是对称函数。引理2.4说明(3.4)和(3.5)是反转解,而
和
不是反转解。
ii) 若
解f无不动点,则f是对称的,依据引理2.4知f是反转解。
注3.1 设
,考虑(1.4)的对偶方程。由定理3.1,除
和
之外,其所有
解
都是反转解。
例3.1 考虑迭代方程
(3.6)
特征方程
的特征根
根据定理3.1,函数(3.4)和(3.5)是方程(3.6)的反转解。此外,(3.6)的无不动点的
解也是反转的。
引理3.3 (定理3.1, [12]) 设
。则方程(1.4)的所有
解
是严格递减的,且有唯一不动点0。
定理3.2 设
,则方程(1.4)无反转解。
证明 根据引理3.3,方程(1.4)的每个
解f严格递减。注意到
皆不等于−1,根据引理2.5,每个
解f都不是对合的。引理2.3说明方程(1.4)的每一个
解f不是反转的。
注3.2 若
,考虑(1.4)的对偶方程,得到每一个
解
不是反转的。
4. 特征根不同号
在这一节,我们研究方程(1.4)在特征根不同号情况下的反转解。
引理4.1 (定理4.1, [12]) 设
(
,
,
)。
i) 若 是方程(1.4)的严格递增解,则f是引理3.1中给出的解。
是方程(1.4)的严格递增解,则f是引理3.1中给出的解。
ii) 若
是方程(1.4)的严格递减解,则
。
定理4.1 设
(
,
,
),方程(1.4)无反转解。
证明 若
是方程(1.4)的严格递增解,根据引理3.1知f不是对称的,因此不是反转解。
若
是方程(1.4)的严格递减解,根据引理4.1有
。注意到
不是对合的,因而不是反转解。
例4.1 考虑迭代方程
(4.1)
特征方程
的特征根
利用定理4.1,得到方程(4.1)无反转解。
注4.1 若
(
,
,
),考虑方程(1.4)的对偶方程,由定理4.1得到方程(1.4)的每一个
解
都不是反转解。
引理4.2 (定理2, [13];定理2, [4]) 设
。
i) 若
是方程(3.1)的
解,则f严格递增。若f有不动点,则 时,
;当
时,
,其中
。
时,
;当
时,
,其中
。
ii) 方程(3.1)的每一个无不动点的
解
由任意的初始函数确定。
引理4.3 (定理4.2, [12]) 设
(
)。
i) 若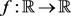 是方程(1.4)的严格递增解,则f由引理4.2给出。
是方程(1.4)的严格递增解,则f由引理4.2给出。
ii) 若
是方程(1.4)的严格递减解,则
。
定理4.2 设
(
)。
i) 方程(1.4)除
之外的所有严格递增的解都是反转解,并且可以由引理4.2构造。
ii) 方程(1.4)的唯一严格递减解
不是反转解。
证明 i) 根据引理4.3,方程(1.4)的严格递增的解f由引理4.2给出并构造。若f没有不动点,则f是对称的,因而是反转的。若f有唯一不动点0,则f属于下面的四种情况之一
(4.2)
(4.3)
或
,其中
。函数(4.2)和(4.3)是对称的,然而
是不对称的,因此(4.2)和(4.3)是反转解,而
不是反转解。
ii) 如果f是方程(1.4)的
严格递减解,引理4.3说明
。因为
不是对合的,所以
不是反转解。
注4.2 若
(
),考虑方程(1.4)的对偶方程,得到与定理4.2相似的结果。
引理4.4 (定理3,定理4, [13];定理3,定理5, [4]) 设
(或
,或
)。若
是方程(3.1)的
解,则f严格递减,且有唯一不动点0,并且满足双边Lipschitz条件
,
且
引理4.5 (定理4.3, [12]) 设
(
,
,
)。
i) 若
是方程(1.4)的严格递增解,则
。
ii) 如果
是方程(1.4)的严格减解,则f由引理4.4给出。
定理4.3 设
(
,
,
),则方程(1.4)无反转解。
证明:由引理4.5可知,方程(1.4)存在唯一的
严格递增解
,注意到
不是对称的,引理2.4说明其不是反转解。若f是方程(1.4)的严格递减解,则由引理4.4-4.5可以构造f。注意到
,根据引理2.3和引理2.5说明f不是反转的。
注4.3 若
(
,
,
),考虑方程(1.4)的对偶方程,可知方程(1.4)无反转解。
引理4.6 (定理4.4, [12]) 设
(
)。
i) 若
是方程(1.4)的严格递增解,则
。
ii) 若
是方程(1.4)的严格递减解,则
或
。
定理4.4 设
(
),则方程(1.4)无反转解。
证明 根据引理4.6,方程(1.4)有唯一的严格递增解
,此解是非对称的,因而不是反转的。
若f是方程(1.4)的严格递减解,引理4.6说明
或
。注意到
或
都不等于−id,由引理2.5知f不是反转的。
注4.4 若
(
),考虑方程(1.4)的对偶方程,因此方程(1.4)无反转解。
5. 临界情况及进一步讨论
首先考虑方程(1.4)的两种临界情况,然后讨论非齐次方程(1.5)的反转解。
引理5.1 (定理6, [11]) 设
,
是方程(1.4)的
解。
i) 若
,则
,其中c是实常数。
ii) 若
,则
。
定理5.1 设
。
i) 若
,则方程(1.4)的每一个
解
是反转的,其中c是实常数。
ii) 若
,则唯一的
解
是反转的。
证明:i) 若
,根据引理5.1,方程(1.4)的所有
解为
。由引理2.4知
是反转解。
ii) 若
,引理5.1说明
是方程(1.4)的唯一的
解。引理2.3和引理2.5说明
是反转的。
以下引理在研究非齐次方程(1.5)的反转解中起到重要作用。
引理5.2 (引理3, [5]) 设特征方程(1.3)的所有根
都是实的。利用代换
方程(1.1)可简化为
反之亦然。
利用引理5.2中的平移变换
,可以得到非齐次方程(1.1)的
解f,即
(5.1)
其中
。因此,根据(5.1)和齐次方程(1.4)的
解,我们可以给出特征根
时非齐次方程(1.5)的所有反转解,下面举例说明。
例5.1 考虑迭代方程
(5.2)
有特征根
,
,
,根据引理4.5,对应的齐次方程
有唯一的严格递增解
,引理4.4说明齐次方程有无穷多个严格递减解
满足双边Lipschitz条件
(5.3)
利用变换(5.1)及常数
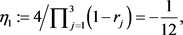
我们得到了方程(5.2)唯一的严格递增解
由于
,不是对称的,因而不是反转的。
另一方面,方程(5.2)的每一个严格递减解
(由
和平移变换
得到),有
。引理2.3和引理2.5说明每一个严格递减解
不是反转的。因此,方程(5.2)没有反转解。
例5.2 考虑迭代方程
(5.4)
由于特征方程
的特征根
,定理5.1说明对应的齐次方程
有唯一的
解
。
通过变换(5.1)及常数
我们得到方程(5.4)的唯一的
解f是
引理2.3和引理2.5说明方程(5.4)无反转解。
基金项目
山东省自然科学基金(ZR2017MA019),滨州学院科研基金(BZXYL1802),滨州学院核心课程(BYHXKC201604)。