1. 引言
近年来,我国对西部地区的开发力度逐渐加大,依次建设完成青藏公路、青藏铁路以及西气东送等多个重点项目,而举世瞩目的川藏铁路工程也被正式提上日程。在西部地区,尤其是青藏高原地区,地质地貌种类复杂多样,开发难度极大,面临包括地形高差、地震频发、山地自然灾害以及冻融作用等诸多地质问题。而其中,冻融作用是影响高寒地区工程设计与建设的关键因素,有关研究结果表明,冻融时的冻胀力,低温时岩石强度的变化以及融化后岩石的强度损失,是灾害产生的主要源头 [1] [2]。因此,研究岩石在冻融循环作用下损伤破坏机制具有重要的工程意义。
冻融作用对岩石力学性质的影响早已引起了国内外研究学者的兴趣。研究学者普遍认为,对于冻融环境中的岩体损伤破坏,是因为岩体受到天然缺陷的影响,冻融损伤的过程实际上是反复的冻胀荷载作用引起的 [3] [4] [5]。因此在现阶段,有关研究大多集中于岩石损伤的识别和鉴定,以及通过对比岩体试验前后的物理力学指标变化,对岩体的损伤状况作出评价。在岩体冻融损伤的识别方面,贾海梁等 [6] 基于SEM技术,观测了冻融环境下砂岩孔隙环境,据此对岩石微观损伤定量分析进行了研究和探索;任建喜等 [7] 基于CT扫描技术,利用自制的三轴CT加载系统,获得了冻结裂隙岩石在加卸荷过程中的CT图像,并分析了其演化结果;李杰林等 [8] 选取寒区花岗岩为试样,利用核磁共振技术,得到了岩样在不同循环次数后的内部微观结构图像;Park等 [9] 以闪长岩,玄武岩和凝灰岩作为样本,在实验室模拟冻融环境,并根据CT图像和SEM图片,研究了岩石的内部微观变化。在试验测试及理论方面,贾海梁等 [10] 通过试验对砂岩的孔隙率进行了研究,并建立了冻融作用下的损伤模型;Gao等 [11] 从耗能的角度研究了砂岩在荷载作用下的破坏机理,并基于此建立了岩石冻融演化模型;Nicholson等 [12] 对10种沉积岩进行冻融试验,并提出了4种岩石劣化模型。
数值模拟在近年来也被大量用来解决岩体裂隙扩展方面的问题,Bahaaddini等 [13] 采用PFC软件对平行多节理的岩体模型进行了模拟,总结出5种岩体破坏模式;李树忱等 [14] 基于弹性损伤力学,利用FLAC3D软件对深部岩体的破裂演化过程进行了模拟分析;汪子华等 [15] 利用FLAC3D研究了节理条数和倾角对节理岩体力学特性的影响;申艳军等 [16] 从理论角度推导出低温下裂隙岩体的冻胀演化解析式,并以Comsol-Multiphysics软件进行了验证。由上述内容不难发现,在试验和理论方面,对于冻融作用对岩石力学性质影响的研究已经相当成熟,而在数值模拟方面却报道不多。因此,本文将基于FLAC3D中的应力–应变软化模型,对单裂隙岩体在冻融荷载耦合作用下的损伤与破坏模式进行模拟与分析。
2. 本构模型与基本参数的选取
2.1. 本构模型的选择
FLAC (Fast Lagrangain Analysis of Continua)是由Itasca公司开发的连续介质仿真计算软件,有二维和三维计算程序两个版本,其中三维计算程序FLAC3D相较于其他软件,采用“混合离散法”模拟塑性破坏和流动,精准度更高;以动态运动方程进行求解,使得模拟过程不存在数值上的障碍;利用显示差分法求解微分方程,便利对系统演化过程的跟踪。
在FLAC3D计算程序中,内置有12种岩土本构模型,在进行数值模拟的本构模型选择时,要根据工程材料的已知力学属性和本构模型的适用范围进行综合考虑。对于岩体裂隙扩展过程的模拟,多采用Mohr-Coulomb模型,其具有计算效率高且模拟效果较好的特点,但是该模型无法直接计算出塑性应变,即不能够模拟岩石达到峰值强度后的应变软化现象,并且无法获得岩石材料的残余强度。而FLAC3D提供的应力–应变软化模型则很好地解决了这个问题,该模型实际上是Mohr-Coulomb模型的衍生,在弹性变形阶段两者的计算结果是相同的,而在达到屈服极限之后,应力–应变软化模型能够很好地模拟出应变软化现象。所以,本文最终选用应变软化模型来进行数值模拟过程。
2.2. 基本参数的确定
在对于模拟试验,所需的参数包括密度ρ,体积模量K,剪切模量G,粘聚力c,内摩擦角φ,抗拉强度σt。在FLAC3D中,使用的变形参数为体积模量K和剪切模量G,这是因为K表征材料的抗体积变形能力,G表征材料的抗剪切变形能力,而通常提供的变形参数是杨氏模量E和泊松比 ,因此需要转化,转换关系如式(1)和式(2)所示:
#(1)
#(2)
本试验采用的粗砂岩初始力学参数见表1。
对于冻融循环后弹性模量的变化,阎锡东等 [17] 根据Mori-Tanaka方法建立了相关的关系式:

Table 1. Initial mechanical parameters of coarse sandstone
表1. 粗砂岩初始力学参数
#(3)
其中 为冻融循环后的弹性模量,E为初始弹性模量,α为裂纹密度参数,表示为 ,a为裂隙半长度,N为单位面积上平均半长度为a的裂纹的数量。
由于试验采用应变软化模型,因此还需要确定岩石参数和峰后应变软化参量之间的关系,由张帆等 [18] 的研究可知,在应变软化过程中,粘聚力的值会随应变软化参量的增大而逐渐减小,而内摩擦角的大小几乎保持不变。则基于上述内容,同时参考田延哲等 [19] 实验室试验的数据和结果,可对各级次冻融循环后的数值模型参数进行计算拟定,共分为四种情况,冻融次数分别为0、30、60、90,对应各参数如下表2所示。

Table 2. Numerical model parameters
表2. 数值模型参数
3. 基于FLAC3D的单轴压缩试验模拟
3.1. 试验方案与模型建立
为同时考虑在冻融环境下不同裂隙倾角对岩体强度和破坏特征的影响,数值模拟试验同时引入了冻融循环次数和裂隙倾角两个变量。取裂隙岩体的裂隙倾角分别为0˚、30˚、60˚、90˚,为了便于对比,还设置了一组完整模型试样。而后对应上述每种模型,分别考虑其在进行了0、30、60、90次冻融循环后的情况进行单轴压缩试验模拟,并记录相应的应力–应变曲线以及塑性区扩展分布图等。
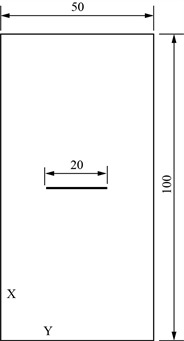
数值模型采用CAD和ANSYS软件建立,根据岩石单轴压缩试验的尺寸比例要求,取模型的尺寸为50 mm × 50 mm × 100 mm。裂隙置于模型的中心位置,且为非贯通型裂隙,即从模型的一侧面起,垂直穿入模型20 mm,裂隙与模型侧面共面部分的长度同样设为20 mm,裂隙厚度为0.4 mm。如图1所示。
在CAD软件中按上述尺寸将模型几何绘制出后,将其导入到ANSYS软件中进行网格的划分。网格划分完毕后,完整岩体模型含134个节点,393个单元;裂隙倾角为0˚时岩体模型含10,334个节点,46,226个单元;裂隙倾角为30˚时岩体模型含11,268个节点,52,070个单元;裂隙倾角为60˚时岩体模型含11,940个节点,55,694个单元;裂隙倾角为90˚时岩体模型含11,596个节点,53,901个单元。图2为其中一种工况下岩体模型的网格划分的情况。
 (a) 0˚裂隙
(a) 0˚裂隙 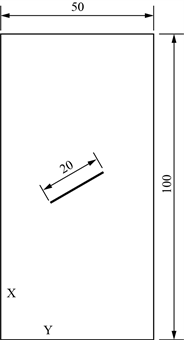 (b) 30˚裂隙
(b) 30˚裂隙 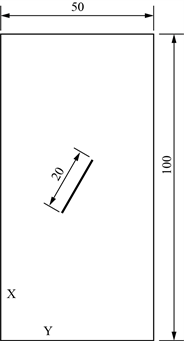 (c) 60˚裂隙
(c) 60˚裂隙 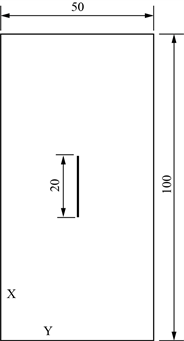 (d) 90˚裂隙
(d) 90˚裂隙
Figure 1. The models with different fracture dip (Unit: mm)
图1. 不同裂隙倾角模型(单位:mm)
3.2. 边界条件与监测点的设定
把网格划分后的模型导入到FLAC3D软件中,并将模型各面进行分组,以便后续边界条件和外荷载的施加与设定。而后将模型的岩石部分定义为应变软化模型,并赋予相应的力学性质参数,至于裂隙部分,则设为空模型。最后,在模型顶面和底面施加荷载,侧面为自由面,采取的加载方式为轴向位移加载,大小为0.0001 mm/s,则后续内容中所提到的运算步实际指的是试验过程中的加载时间,即1步等于数值模拟试验中的1 s。以裂隙倾角为0˚时的模型为例,边界条件设定后的模型见图3。
Figure 3. The numerical model after boundary conditions are set
图3. 边界条件设定后的模型
为了获得岩体模型的应力–应变曲线,故在模型顶部设监测点,分别为P1 (25,25,100),P2 (0,0,100)。其中,在P1点处同时监测其z向位移和应力;在P2点处仅监测其z向应力。根据有限差分法的相关理论,可知顶面各点处的位移可以认为是相同的,故可用P1点处的位移来代表整个顶面的位移。至于应力,由于顶面各点处应力均不相同,故采用平均应力进行代替。
4. 结果分析
4.1. 不同冻融循环次数下裂隙岩体的损伤破坏特征
根据实验方案,在每种裂隙倾角条件下均分别进行了4组实验,但限于文章篇幅,在下述部分内容中仅列出了其中几组具有代表性的数据结果。为了分析结果更加全面,将从应力–应变关系曲线、峰值强度、残余强度以及塑性区分布等三个不同方面进行对比总结。
1) 应力–应变关系曲线
以完整模型和裂隙倾角为30˚时模型的模拟结果为例,将得到的各级冻融循环次数下的岩体应力–应变曲线综合绘制在同一坐标系下,并进行对比分析,相关图像如下图4、图5所示。
根据上述曲线,经过对比可知在历经不同冻融循环次数后,模拟结果中岩体的应力–应变曲线的形态是基本相同的,但可以明显看到峰值应力、残余应力以及弹性段的倾角都随冻融循环次数的增加而相应减小。
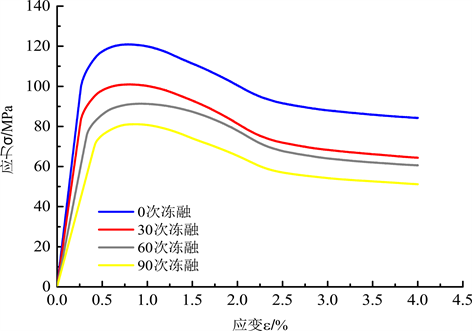
Figure 4. Stress-strain curve of the complete rock mass
图4. 完整岩体应力–应变关系曲线

Figure 5. Stress-strain curve of rock mass with 30˚ fractured
图5. 裂隙倾角为30˚时岩体应力–应变关系曲线
2) 峰值强度与残余强度
将每种工况下模拟所得到的岩体峰值强度和残余强度提取出来,并以冻融循环次数为横轴,峰值强度和残余强度竖轴分别绘制点线图,进行对比分析。如图6和图7所示。
根据上述曲线,经过对比可知,岩石的峰值强度和残余强度都会随着冻融循环次数的增加而发生明显的下降。此外,经过计算可以得到,在历经30次、60次以及90次冻融循环后,对于完整岩石,其峰值强度损失率分别为16.46%,24.44%,32.85%,残余强度损失率分别为23.58%,28.08%,39.26%;对于0˚裂隙岩体,其峰值强度损失率分别为16.74%,24.44%,31.01%,残余强度损失率分别为24.50%,27.58%,34.75%;对于30˚裂隙岩体,其峰值强度损失率分别为17.08%,25.23%,31.45%,残余强度损失率分别为24.73%,27.52%,35.46%;对于0˚裂隙岩体,其峰值强度损失率分别为16.67%,24.24%,31.11%,残余强度损失率分别为26.79%,29.46%,37.06%;对于90˚裂隙岩体,其峰值强度损失率分别为16.64%,24.16%,29.90%,残余强度损失率分别为22.38%,27.86%,38.22%。
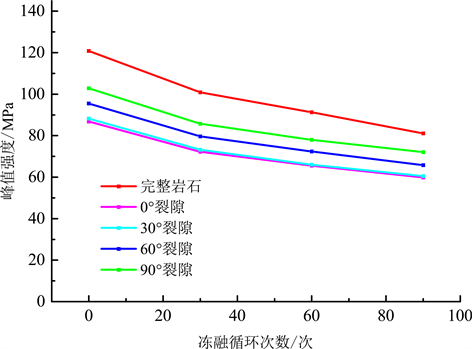
Figure 6. Relationship between peak strength and the number of freeze-thaw cycles
图6. 峰值强度与冻融循环次数关系图
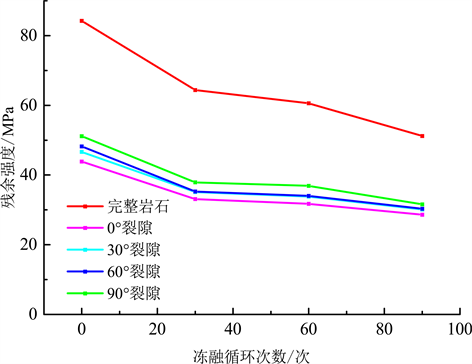
Figure 7. Relationship between residual strength and the number of freeze-thaw cycles
图7. 残余强度与冻融循环次数关系图
对比分析上述峰值强度和残余强度在各级冻融循环之后的损失率,可知峰值强度和残余强度在前30次冻融循环后都发生了明显的下降,在之后峰值强度的下降趋势渐于平缓,而残余强度在中间30次循环过程中几乎没有变化,再之后才又开始缓慢降低。
3) 塑性区扩展分布情况
通过分析塑性区的发展与分布情况可以更好的总结裂隙岩体在冻融荷载耦合作用下的破坏特征,由于试验组数较多,此处仅列出裂隙倾角为30˚的岩体在经过0次(即无冻融作用)和90次冻融循环后,加载过程中的塑性区的发展情况。如下图8和图9所示。
对比上述图片可知,冻融循环次数对于塑性区的发展规律不会造成影响。塑性区均是从裂隙的两个部端的上下两侧开始萌生,并分别沿着与水平面近似夹角为45˚与135˚的方向逐渐向外扩展,直至到达岩体侧壁,最终在岩体两侧形成以裂隙为中心的“W”型塑性区域,并造成岩体损伤破坏。不同的是,经历多次冻融后的裂隙岩体,其塑性区的发展速度有较为明显的提升,扩展范围也有一定程度的增大。
由上述可见,尽管所采用的数值模型无法将岩体在冻融循环作用下所受到的各种力学效应考虑在内,但相应的模拟结果已经从很大程度上反映出冻融循环作用对于岩石损伤破坏所造成的影响,满足了对比分析的基本要求。
4.2. 不同裂隙倾角下岩体的冻融损伤破坏特征
同样基于控制变量的思想进行对比分析,与分析冻融循环次数对于岩体的损伤破坏特征所采取的角度一样,将从应力–应变关系曲线、峰值强度、残余强度以及塑性区分布等三个不同方面进行总结。
1) 应力–应变关系曲线
以进行了0次(即无冻融作用)与90次冻融循环后的模拟结果为例,将得到的不同裂隙倾角条件下的裂隙岩体应力–应变曲线综合绘制在同一坐标系下,并进行对比分析,相关图像如下图10和图11所示。
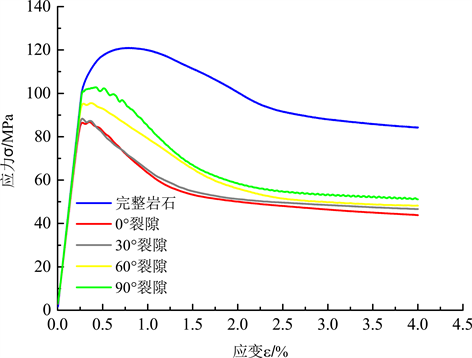
Figure 10. Stress-strain curve after 0 freeze-thaw cycles
图10. 0次冻融循环后应力–应变关系曲线
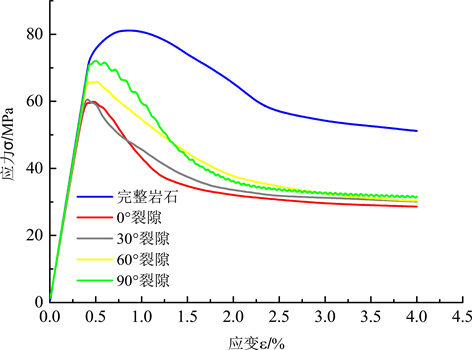
Figure 11. Stress-strain curve after 90 freeze-thaw cycles
图11. 90次冻融循环后应力–应变关系曲线
对比上述曲线可知,在同样的冻融循环次数条件下,各曲线的走势基本相同,但裂隙的存在会明显降低岩石的强度,0˚裂隙倾角和30˚裂隙倾角的曲线几近相同,且较早到达强度峰值;不同倾角下的裂隙岩体的应力–应变关系曲线随着加载的进行而趋于重合。
2) 峰值强度与残余强度
相关曲线与上文图6和图7相同,根据4.1相应部分对于峰值强度与残余强度的分析结果,可知不同裂隙倾角下,岩体强度的损失率十分接近;0˚裂隙倾角和30˚裂隙倾角对应的岩体峰值强度较小,随着裂隙角度的增加,峰值强度会有较为明显的回升。
3) 塑性区扩展分布情况
取历经90次冻融循环后的不同裂隙倾角岩体,在模拟加载了16,000步后的塑性区发展情况为例,进行对比分析,如图12所示。
 (a) 0˚
(a) 0˚  (b) 30˚
(b) 30˚  (c) 60˚
(c) 60˚  (d) 90˚
(d) 90˚
Figure 12. Plastic zones distribution of rock mass with different fracture dip angles after 90 freeze-thaw cycles
图12. 90次冻融循环后不同裂隙倾角岩体塑性区分布图
通过上图对比,可知裂隙倾角对于塑性区的扩展范围具有十分明显的影响,随着裂隙角度的增大,塑性区的发展范围也随之增大,但塑性区基本上均呈对称分布的“W”型结构,证明不同裂隙倾角下岩体的损伤机理与破坏特征是一致的。
5. 结论
通过利用数值模拟方法,分别对不同裂隙倾角下和不同冻融循环次数下的单裂隙岩体冻融损伤破坏特征进行综合对比分析,可以得到以下结论:
1) 相同裂隙倾角条件下,在历经不同冻融循环次数后,岩体的应力–应变曲线形态是相同的,但峰值应力、残余应力以及弹性段的倾角都随冻融循环次数的增加而相应减小。此外,岩体峰值强度和残余强度在前30次冻融循环后下降明显,之后峰值强度下降趋势渐于平缓,而残余强度在中间30次循环过程中几乎没有变化,之后又开始缓慢降低。
2) 相同冻融循环次数下,不同裂隙倾角对岩体强度的影响程度有所差异,0˚裂隙倾角和30˚裂隙倾角对应的岩体峰值强度较小,影响显著,但随着裂隙角度的增加,岩体峰值强度会有较为明显的回升。
3) 在冻融荷载耦合作用下,裂隙岩体的破坏特征与常规条件下的规律是一致的,但是冻融作用的存在会大大加速裂隙岩体的破坏进程。
基金项目
山东省交通厅科技发展计划(2019B47_1)和国家自然科学基金(51879149)。