1. 引言
习近平总书记明确提出“节水优先,空间均衡,系统治理,两手发力”的治水思想,强调要通盘考虑重大水利工程建设,更多运用成熟适用技术等 [1]。李克强总理在2015年两会期间政府报告会上指出“能源生产和消费革命,关乎发展与民生”,并提出“要积极发展水电”的要求。21世纪以来,我国各种大中型水电站的建设兴起,如西部大开发实施,南水北调工程、长江三峡工程、黄河小浪底工程等。这些水电工程大多修建在我国西部及西南地区,以地下厂房的形式存在于复杂的地质环境中,加之岩体介质的复杂性,使得工程难度增大,灾害频发,水电资源开发面临挑战。
据统计目前在全球的可再生能源发电领域内水电的比重高达80%,在中国,这一比例更是接近于85%,所以水电是全球替代化能源的第一主力 [2]。我国水电资源总量位居世界第一,但开发利用水平较低,具有较大的开发潜力。根据我国“十三五”相关规划信息,中国2020年力争常规水电装机达到3.5亿千瓦左右,2020年前重点开发雅砻江、大渡河、金沙江、澜沧江等河流,2020年后重点开发怒江和雅鲁藏布江,中国的水电建设即将迎来新一次的发展高潮。
我国西南部及沿海地区水资源较为丰富,所以水电工程大多修建在西南及沿海地区。这些水电工程的发电系统通常修建在地下岩体内,采用深埋的大型地下洞室群结构,在水利发电枢纽中具有多个相互平行的地下主厂房、主变室和尾闸室等相邻洞室。而我国这些水电工程大多集中在西南部地区,处于高山峡谷等复杂的地质环境中,埋深较深,规模较大,空间结构复杂。并且岩体介质性质特殊,具有不确定性和多变性,使得开挖过程具有很大的未知性。同时,大型地下洞室群的分步开挖伴随着围岩的应力重分布,是一个动态不可逆的过程,存在着各种未知的风险。
复杂的地质情况导致我国的大型地下洞室的开挖过程事故频发,如福堂、锦屏二级、金平水等水电站发生过多次岩爆事故 [3] [4] [5] [6],溪洛渡、锦屏一级、立州等水电站发生过局部塌方、岩体错位、变形较大、混凝土开裂等事故 [7] [8] [9]。
正如世界上没有两片完全一样的树叶,也没有两个完全一样的地下工程,可见地下洞室工程具有复杂性、独特性和未知性。因此,对于大型地下洞室群分步开挖稳定性的研究对工程安全和国家的发展都具有重要意义。
综上所述,进行大型地下洞室群分步开挖稳定性的数值模拟研究具有较大的理论价值与工程意义,助力中国水电建设事业的顺利发展。
2. 国内外研究现状
随着国家经济、科学技术的不断发展,水电工程的规模也越来越大,地下洞室群作为水电站的主体建筑,由许多相互连通的厂房洞室组成,其规模也逐渐扩大,结构日趋复杂,加之所处的地质条件复杂性,使得洞室开挖过程中围岩稳定性问题突出。
2.1. 国内研究现状
国内外学者对于地下洞室围岩稳定性的研究还没有形成系统全面的方法,大多是依托具体工程案例进行综合分析或是依靠经验。
在数值模拟分析方面,国内学者陈浩等 [10] 通过基于三维弹塑性有限元数值计算理论的ABAQUS软件进行大型地下洞室群分期开挖围岩稳定性的研究。
左双英、李洁等 [11] 利用FLAC 3D数值分析软件或三维拉格朗日分析方法,对水电站地下厂房复杂洞室群进行开挖支护模拟,分析了在无支护和系统支护工况下,开挖完成后围岩的位移场、应力场、塑性区等的分布特征和演化规律。
朱维申 [12] 等用数值模拟方法研究了不同岩类、埋深、侧向地应力条件下洞壁位移量的变化规律,并得出预测围岩位移量的拟合多项式,以此为基础提出了作为围岩稳定性判据的相对位移量的具体数值。
郑颖人 [13] 等提出了一种基于半解析元法的三维弹塑性围岩稳定性分析方法。
杨典森等 [14] 应用FLAC 3D方法,研究地下洞室群在开挖、支护过程中围岩变形及支护结构的受力特点。
在综合方法方面,邱道宏等 [15] 采用数值计算和现场监控测量的方法,分析大型地下洞室分步开挖围岩稳定性,并以此来预测岩爆发生情况。
孟国涛等 [16] 通过室内岩石力学试验与FLAC 3D相结合的方法,分析洞室开挖过程中的围岩应力集中区;通过3DEC与位移监测相结合的方法进行围岩支护措施分析;并通过研发的Comba本构模型与声波检测结合的方法,研究柱状节理围岩稳定性。
撒文奇等 [17] 以数值模拟技术为基础,建立现场施工的动态仿真,并提出地下洞室群围岩劣化损伤折减计算方法。
在创新方面,苏国韶等 [18] 以三维弹塑性数值计算为基础,提出智能优化方法研究高地应力条件下的地下洞室群开挖围岩稳定性。李建贺等 [19] 提出了用特征角和应力扰动指标SDI来表征洞室围岩的应力场受到扰动的程度大小。吴杉 [20] 对地下洞室群的施工方案进行动态规划,以达到优化围岩稳定效果的作用。高玮等 [21] 创新提出了蚁群算法来处理地下洞室群开挖顺序的组合优化问题。陈明等 [22] 从施工全过程的不同方面进行优化来提高洞室开挖围岩稳定性。黄仁东等 [23] 以熵权法和理想点法为原理进行围岩稳定性研究。
2.2. 国外研究现状
Johansson等 [24] 对不同结构类型的岩体行为进行三维的反演计算分析,着重讨论了节理岩体的反演分析,并指出合理的岩体参数对于更好地理解开挖过程中的复杂岩体行为的重要性。
Jiao等 [25] 运用三维离散元法和三维有限差分法,对于节理对冲击波在节理岩体中的传播衰减规律的影响进行了数值模拟,认为三维离散元分析法能够捕捉冲击波的关键特征,并形象模拟节理,作为一种非连续变形分析方法,具有三维有限差分和二维分析方法不可替代的优点。
Ramamurthy等 [26] 运用相似材料模型试验,来模拟顶板的稳定性,探究变形、屈服强度、应力变化等规律,并总结出相应函数模型进行顶板变形及压力分布的预测。
N. M. Syrnikov等 [27] 考虑人为因素对岩体变形状态变化的影响,对地下洞室开挖过程中围岩塑性发展和应力状态的流变过程进行数值模拟,为岩体行为的预测提供了依据。
Sitharam等 [28] [29] 提出了一种简单实用的等效力学模型方法来表征岩体的强度和稳定性。这种方法基于大量的统计分析得到岩石强度与稳定性的关系,将节理岩体表示为等效连续体,这种开发模型被并入到非线性有限元代码中进行等效分析。基于此模型模拟节理岩体中的开挖过程,并运用到三个工程实例当中得到了验证。
Lee等 [30] 运用现场仪表和三维数值分析联合的方法来进行全过程掌控,利用现场仪表动态监测大型地下洞室开挖之前,之中和之后的掌子面三维应力变化和完整的位移历史,进行后监测分析,利用三维数值分析法检验岩体力学行为及开挖推进效果。
Stabel等 [31] 也进行了工程勘察,设计和施工全过程监测和测量,并将第一阶段的大型洞穴建设过程中吸取的经验教训应用于扩建一座额外的洞穴当中。
Hibino等 [32] 运用现场试验的方法测量分析了大型地下洞穴开挖过程中节理岩体的各向异性行为,探究岩体行为与洞穴尺寸规模的关系。
3. 工程概况
该地区工程岩体结构为层状结构,地下泵站系统以III类围岩为主,局部分布有IV类围岩,以页岩为主。主泵室部位III类围岩约占85%;IV类围岩约占15%。下泵站范围内发育的裂隙有两个显著的特点:首先就是NE向陡倾角裂隙发育,其次为垂直NE向一组NW向裂隙发育,缓倾角裂隙主要为层间裂隙。结构面多泥钙质充填或无充填。
本工程由引水干线、灌区工程、工业和城镇供水工程三部分组成。引水干线主要建筑物包括进水塔、隧洞、地下泵站、连通洞及补水泵站、调蓄库及末端出水池。
本工程为II等工程,取水口、引水隧洞为2级建筑物,地下泵站为1级建筑物。
工程取水枢纽从取水口至出水池段,沿线长约6.2 km,设计取水流量20 m3/s,泵站装机容量8.4万kW。包括取水口、引水隧洞(1#隧洞)、调压井、引水压力管道、地下泵站、出水压力管道、出水池建筑物。
本区地震动反应谱特征周期值为0.40 s,地震动峰值加速度值山前大断裂以东为0.10 g,地震基本烈度为VII度。
地下泵站厂区主要建筑物由地下泵站(包括主泵房、副厂房和安装间)、通风机室、出水阀室、电缆竖井及连接洞、交通洞、通风洞、灌浆排水廊道、地面厂区等建筑物组成。安装间布置在主泵房右侧,副厂房布置在左侧,出水阀室布置在地下泵站厂房下游侧,距厂房净距20 m。为水泵电动机及变频启动装置供电的10 kV电缆从地面厂区的综合设备楼通过电缆竖井及连接洞引接。交通洞进口位于厂房右端,进入安装间。通风洞进口位于地面厂区平台西侧,从左端进入与厂房顶拱相连的2#通风机室。
4. 三维数值模拟
采用FLAC 3D对地下厂房洞室群在分步开挖过程中的稳定性进行模拟计算。为了分析洞室群开挖步序的合理性,对比研究了三种开挖顺序下的地下洞室群围岩在分级开挖过程中位移场、应力场分布规律及围岩塑性区演化规律,揭示可能的围岩失稳方式及失稳部位,并得出最优方案。
4.1. 开挖方案
根据工程实际与工程经验,地下洞室采用分层开挖的方式。地下厂房边墙不同高程分别与交通洞、通风洞、泵站支洞等洞室相贯通,开挖中按照小洞贯大洞(室)即小洞提前进入大洞的原则进行开挖。小洞洞口先进入厂房,再进行厂房边墙的开挖。
洞室群分步开挖三大开挖顺序方案为:1) 主泵室与出水阀室同步进行;2) 主泵室与出水阀室同高程开挖;3) 主泵室与出水阀室不同步错层施工。三种开挖方案开挖位置如下图1所示。
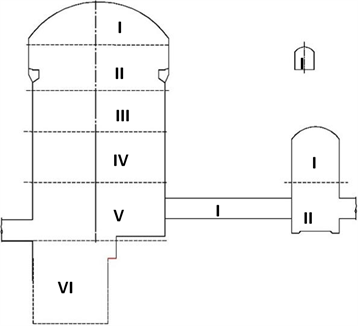
Figure 1. Schematic diagram of the excavation sequence plan for the section of the cavern group
图1. 洞室群剖面开挖顺序方案示意图
4.2. 相关参数选择
在模型建立过程中,模拟了4#机组的主泵房、出水阀室、灌浆排水廊道、泵站1号、2号、3号支洞等,以及考虑对主泵房、出水阀室稳定影响较大的破碎带。相关参数的选择如表1所示。

Table 1. Rock mechanical parameters
表1. 岩体力学参数
4.3. 网格与关键点
经过前期三维初始地应力反演拟合计算,在包括厂房及出水阀室的中心区域,在x方向的侧压系数Kx约1.003,而Ky在y方向则为1.4左右。
4#机组三维模型共划分141,246个单元,27,583个节点。4#机组厂房网格图如图2所示。
为了进一步说明地下厂房各工程部位在分级开挖过程中的应力、变形特征,对各机组段的横剖面,分别在主泵室、出水阀室中选择代表性的特征点,提取特征点的位移、应力量值。各机组段特征点示意图参见图3。

Figure 2. 4# grid division diagram of unit workshop
图2. 4#机组厂房网格划分图
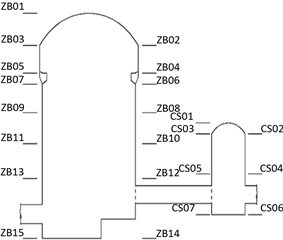
Figure 3. Number and location of key points of excavation
图3. 开挖关键点编号和位置
5. 模拟结果分析
5.1. 位移变化结果分析
主泵室和出水阀室各个关键点的最终位移具体计算位移值如表2所示。

Table 2. The final displacement values of key points in the main pump room and outlet valve room (unit: mm)
表2. 三种开挖方案主泵室、出水阀室关键点最终位移值(单位:mm)
各方案开挖后的总位移云图如图4~6所示。
从图7各关键位置的最终位移可以看出,三个开挖方案总体规律一致。主泵室水平位移最大值均出现在边墙ZB10和ZB11处,垂直位移最大处均在拱顶及拱脚部位,但开挖方案二小于开挖方案一、三。
出水阀室水平位移最大值均出现在下游边墙CS04处,垂直位移最大值均出现在上游拱脚CS07处,
总体来说方案二扰动最小。
如上述,方案二优于方案一、三。
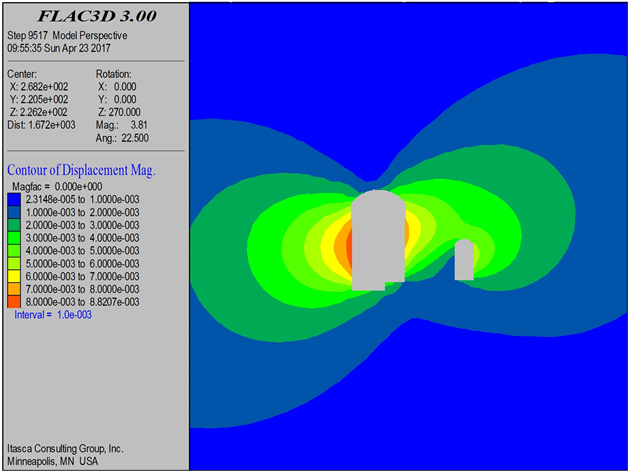
Figure 4. Plan 1 total displacement cloud map
图4. 开挖方案一总位移云图

Figure 5. Plan 2 total displacement cloud map
图5. 开挖方案二总位移云图
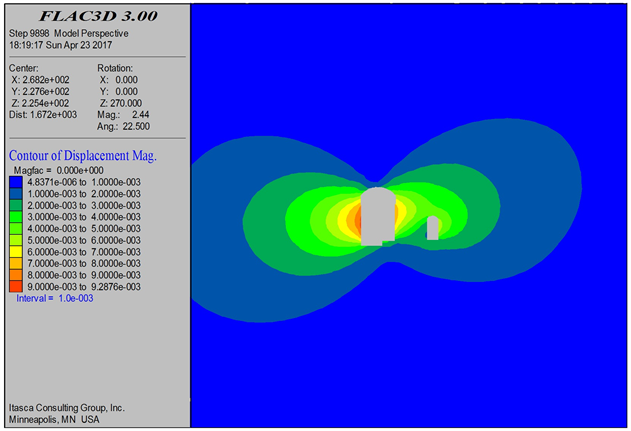
Figure 6. Plan 3 total displacement cloud map
图6. 开挖方案三总位移云图
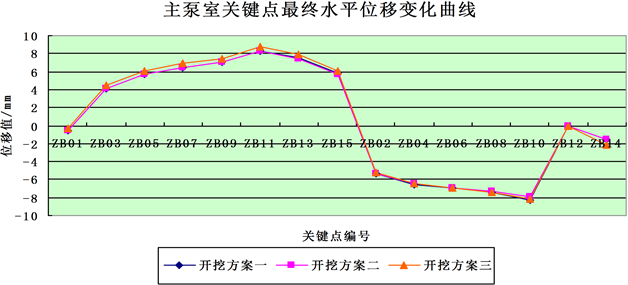
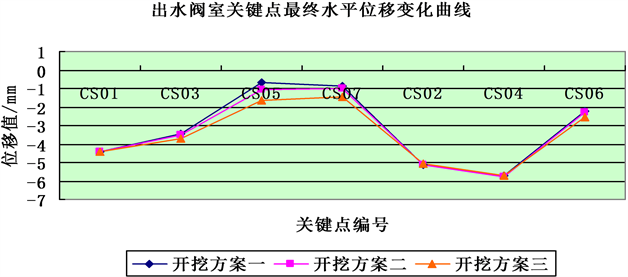
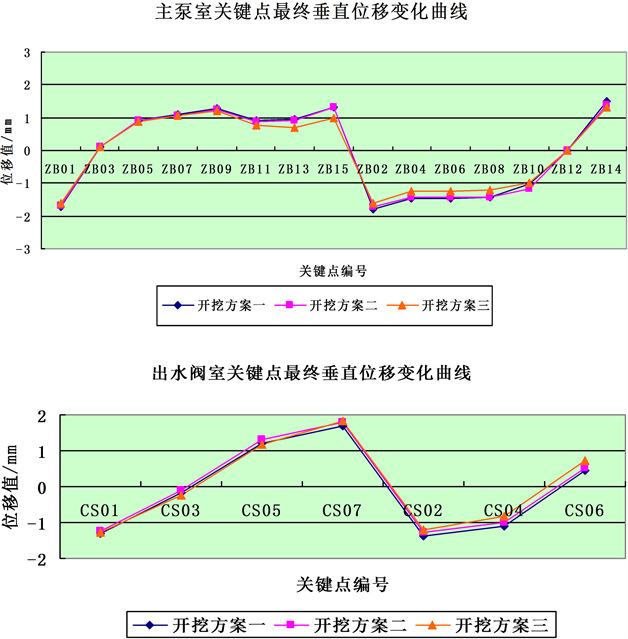
Figure 7. The final displacement curve of key points in the main pump chamber and the outlet valve chamber
图7. 主泵室和出水阀室关键点最终位移变化曲线
5.2. 应力变化结果分析
主泵室和出水阀室各个关键点具体计算最大、最小主应力值如表3~4所示。


Table 3. Stress change table of key points around the main pump room of each staged excavation plan (unit: MPa)
表3. 各分期开挖方案主泵室周边关键点应力变化表(单位:MPa)

Table 4. Stress change table of key points around the outlet valve chamber of each staged excavation plan (unit: MPa)
表4. 各分期开挖方案出水阀室周边关键点应力表变化(单位:MPa)
说明:表中应力拉为‘+’,压为‘−’。
三种方案开挖后的应力云图如图8~10所示。
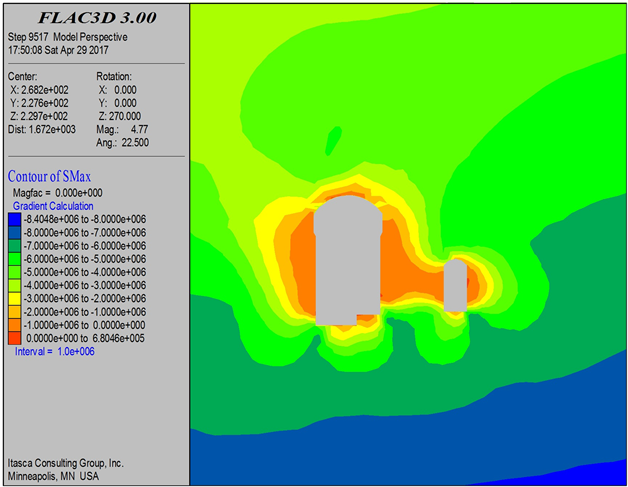
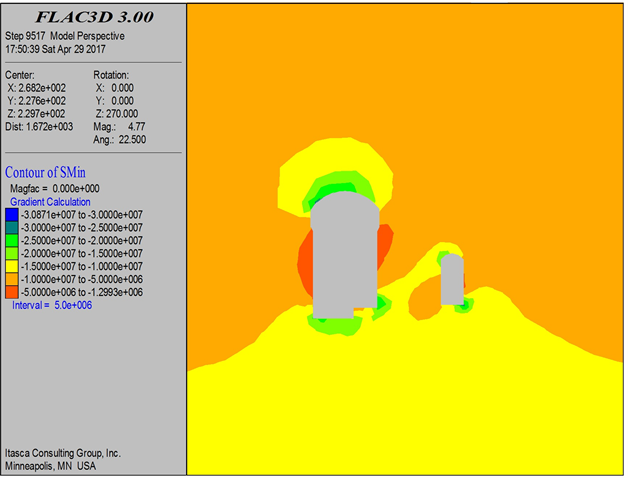
Figure 8. σ1, σ3, cloud map after excavation of the main plan one
图8. 主方案一开挖后σ1、σ3云图
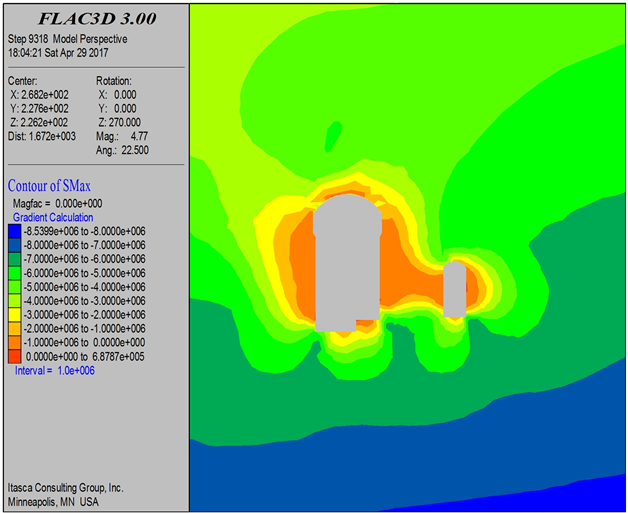
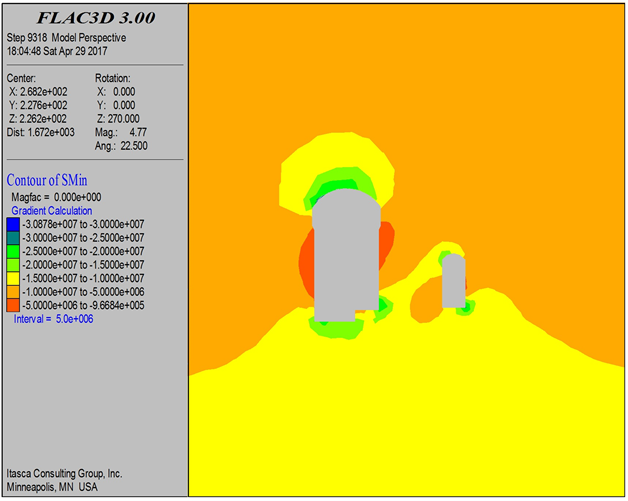
Figure 9. σ1, σ3, cloud map after excavation of the main plan two
图9. 主方案二开挖后σ1、σ3云图
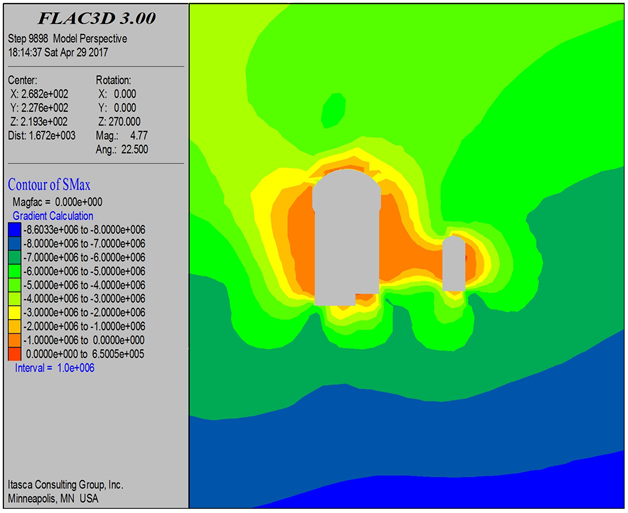
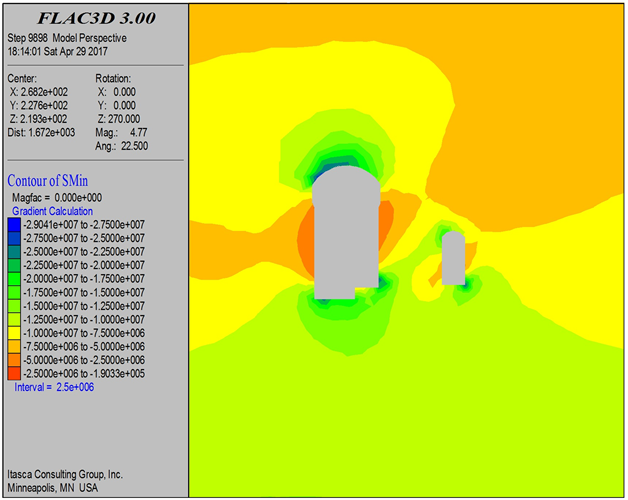
Figure 10. σ1, σ3, cloud map after excavation of the main plan three
图10. 主方案三开挖后σ1、σ3云图
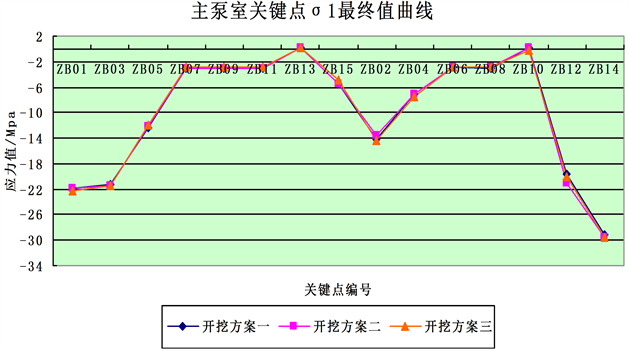
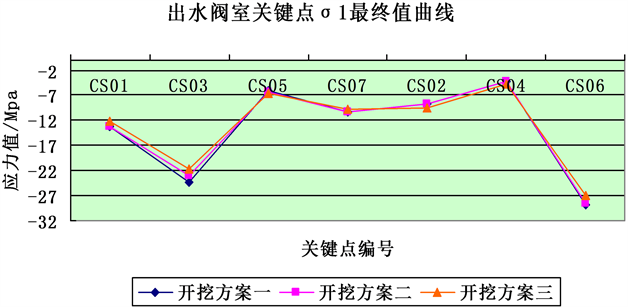
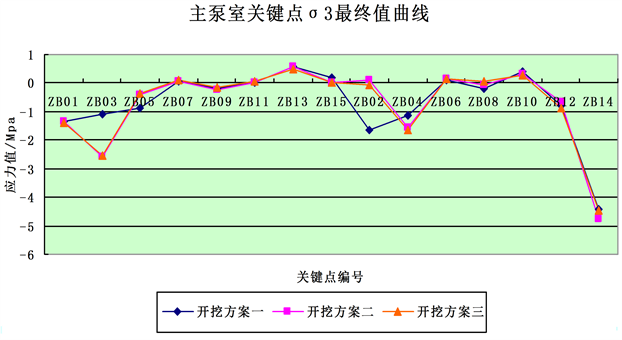

Figure 11. σ1, σ3, final value change curve of main pump chamber and outlet valve chamber
图11. 主泵室与出水阀室σ1、σ3最终值变化曲线
由图11可以看出,主应力基本上都为压应力。三种开挖方案,主泵室围岩应力分布规律基本一致,数值接近,下游中部受断层破碎带的影响而出现较大的应力集中;主泵室应力最大点为拱脚ZB14,σ1均在−29.5 MPa左右,σ3均在−4.5 MPa左右;其次σ1较大的是拱顶ZB01、边墙ZB03与ZB12,均在−22 MPa左右;边墙ZB10与ZB13出现较小的拉应力。
三种开挖方式,出水阀室最终应力分布基本一致,数值相差不大;σ1较大的是拱脚CS06和上游边墙CS03,分别达到大约−28 MPa和−23 MPa。
5.3. 塑性区变化结果分析
三种开挖方案洞室围岩塑性区范围如图12~14。
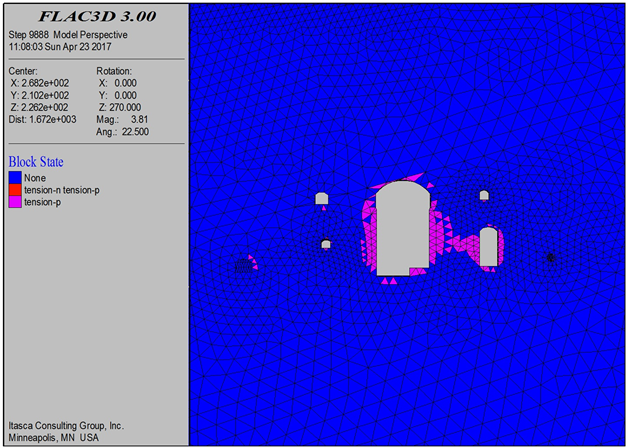
Figure 12. Plan 1 surrounding rock plastic zone range
图12. 开挖方案一围岩塑性区范围
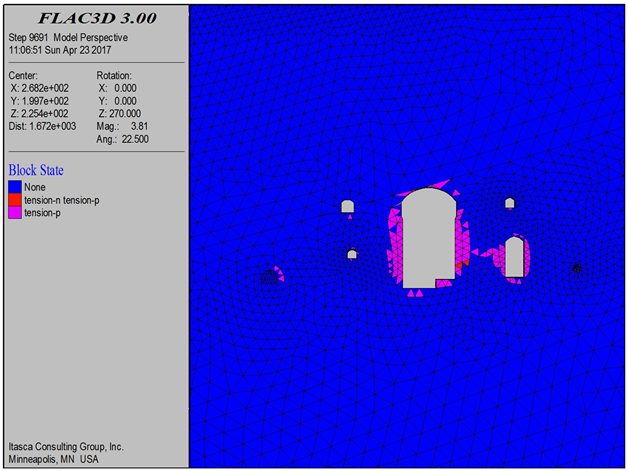
Figure 13. Plan 2 surrounding rock plastic zone range
图13. 开挖方案二围岩塑性区范围
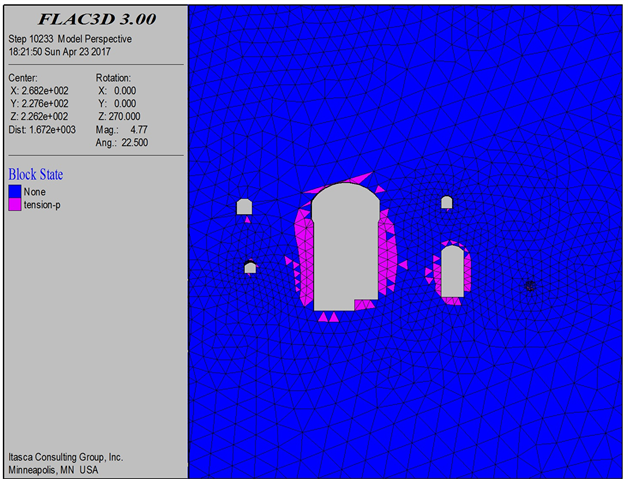
Figure 14. Plan 3 surrounding rock plastic zone range
图14. 开挖方案三围岩塑性区范围
由图12~14可以看出,洞室周围塑性区主要集中在边墙部位,主要为拉伸破坏,开挖方案一主泵室与出水阀室塑性区连通较多,开挖方案二、三塑性区连通较少。

Table 5. The volume change table of the plastic zone around the cavern of each step-by-step plan (unit: m3)
表5. 各分步开挖方案洞室周边塑性区体积变化表(单位:m3)
由表5中的分步开挖过程中的塑性区变化可以看出,在无支护条件下三种开挖顺序中,方案一的主泵室塑性区体积、出水阀室塑性区体积和塑性区总体积都较大,方案二、方案三的各项塑性区体积较小,对周围围岩的扰动较小。

Table 6. Comparison of the depth of plastic zone in the main pump room of the three excavation schemes (unit: m)
表6. 三种开挖方案主泵室塑性区深度比较(单位:m)
由表6各种支护方式主泵室塑性区深度比较可看出,开挖方案一塑性区深度最大,方案二、三较小。
综上所述,开挖方案一塑性区范围较大,对洞室围岩扰动较大,方案二、三塑性区范围较小,扰动较小。
5.4. 小结
三种开挖方案围岩稳定总体规律是一致的,方案二和方案三差别不大且围岩相对方案一较为稳定,但开挖方案二较方案三稍好些,理由如下:
1) 方案二、方案三洞周位移相对方案一小;
2) 方案一、方案二、方案三洞周应力分布和变化差别不大;
3) 方案二、方案三洞周塑性区范围相对方案一小;
4) 方案一、方案二分6步进行,方案三分8步进行,方案一、二步数较少,节省工时。
6. 结论
对于围岩稳定性的研究目前大多是依据具体工程进行分析,不具有普遍借鉴意义,对于进行较为系统的研究,总结出更适合大多数工程的规律,应是以后有待进一步研究的课题。基于西部某水电站厂区工程工程,得出了以下结论:
1) 模拟具有局限性。洞室施工应遵循边开挖边支护的原则,以保证围岩稳定性,本文只进行了开挖而没有进行支护,方便了进行开挖方案的比选,但是与实际工程不符,应在进行不同开挖方案的时候加上支护的内容。
2) 围岩稳定性研究有较多方法,其中数值模拟方法方便、灵活,基于快速拉格朗日分析的FLAC 3D数值计算是地下洞室围岩稳定的有效分析方法。本文即通过FLAC 3D数值计算模拟出不同的开挖顺序,通过对比得出最优的开挖方案。
3) 对计算结果进行分析,研究无支护条件下洞室群围岩的变形、洞周应力及塑性区范围变化规律;评价不同开挖步序的合理性,得出最优开挖顺序方案,并提出开挖过程中重点监测部位。
基金项目
山东省交通厅科技发展计划(2019B47_1)和国家自然科学基金(51879149)。