1. 引言
电学全息方法是一种用来判断特定空间区域内介质分布与特性的现代物理方法 [1]。电学全息过程是指在空间区域周围布置一定数量的、具有多种工作模式的传感器,传感器之间相互实现电学全息波的发射和接收,对传感器采集到的电学全息数据进行数学运算和组合变换,得到抽象的介质属性信息,并将抽象信息具体化的过程 [2]。
电学全息敏感场反映的是空间区域内各个位置对电学全息过程的响应程度,与各个位置处介质的电学参数密切相关 [3]。文献 [4] 报道了一种在极坐标下由电学全息波关于极径的偏导数表达的全息敏感场(本文称之为“极径敏感场”),相比传统单模态敏感场,极径敏感场更加兼顾了幅度和相位敏感性,有效提高了计算精度和效率。基于极径敏感场实施电学全息过程所得的空间区域内的介质分布更加吻合实际 [5]。
以上开展的极坐标分析不由得令人对辐角敏感场(即由电学全息波关于辐角的偏导数表达的全息敏感场)的物理意义展开联想。本文首先建立一种适用于极坐标分析的电学全息模型,然后在模型中构造一种传感器工作模式,计算与模式相匹配的辐角敏感场,意在阐明辐角敏感场能够在提取电学全息波传播轨迹中发挥一定的作用,这对于传播轨迹不是直线的、具有软场效应的波传播问题而言是难能可贵的。
2. 电学全息模型
2.1. 物理结构
本文建立的电学全息模型的物理结构如图1所示。关注的空间区域半径为0.0500 m。在空间区域外,16个电学全息传感器环向均匀布置。所有传感器外围笼罩一个内径为0.0555 m、外径为0.0560 m的有机玻璃筒,将电学全息波束缚于筒内。
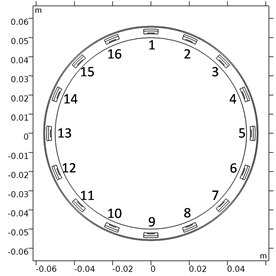
Figure 1. Physical structure of electric holographic model
图1. 电学全息模型的物理结构
2.2. 传感器工作模式
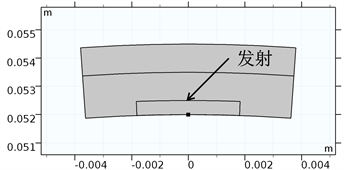
以1号传感器发射、5号传感器接收为例进行说明。如图2所示的传感器局部结构,传感器材料由外向内分别是金属、绝缘体、金属,发射体、接收体、接地体均位于绝缘体内镶嵌的金属材料的外边界。特别地,为了与先前报道形成鲜明对比,图2(b)称作“接收和接地功能合一的工作模式”。
 (a)
(a) 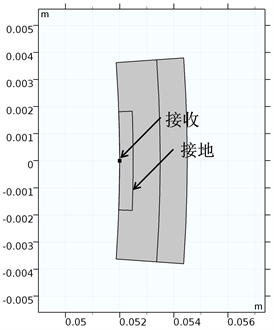 (b)
(b)
Figure 2. Working mode of electric holographic sensor. (a) No. 1 sensor; (b) No. 5 sensor
图2. 电学全息传感器工作模式。(a) 1号传感器;(b) 5号传感器
2.3. 数学表达
假定发射的电学全息波具有适当的频率,既能够明显体现不同介质带来的相位差异,也使得相位变化控制在一个周期以内,不会发生“相位缠卷”。在图1所示的物理结构下,当电学全息波频率处于MHz量级时,一般均可满足上述要求 [6]。此时电学全息模型的数学表达 [7] 为:
(1)
其中,
为电学全息波,为复数,V;D为关注的空间区域;
为区域内的复介电常数,F/m;
泛指发射传感器;
泛指接地传感器。以往文献所需的电学全息数据通常为接收传感器
上的
值,与本文讨论的内容无关。在合理的电学全息波频率范围内,空间区域D内的介质
值可近似为实数,通常处于1~100,同时为了突出电学全息波对介质的电学参数的响应程度,传感器的
值可假定为纯虚数,其虚部通常处于0.1~10。在给定的参数设置下,式(1)可通过有限元等方法求解。
3. 辐角敏感场
3.1. 数学表达
在极坐标系下,电学全息波的梯度满足
(2)
文献 [4] 报道的极径敏感场取式(2)的
分量,即
(3)
类似而又特殊地,本文引入的辐角敏感场取式(2)的
分量,但为避免与先前报道重复论述,这里不再分别讨论实部和虚部的影响,即
(4)
式(4)可在式(1)的基础上求解。
3.2. 初步试算
仍然以1号传感器发射、5号传感器接收为例,令空间区域D内的介质
值恒为1,计算与之相匹配的辐角敏感场,结果如图3所示。主要结论有三:
(1) 辐角敏感场在发射、接收传感器之间的劣弧周围具有较强的响应程度;
(2) 电学全息波传播轨迹通常为弧线而非总是为直线,深化了对电学全息波软场效应的认识;
(3) 辐角敏感场在电学全息波传播轨迹处的响应程度最弱,为提取电学全息波传播轨迹提供了依据。
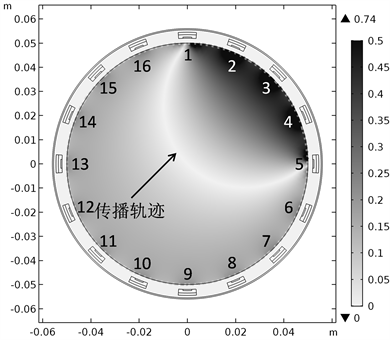
Figure 3. Phase sensitivity field when No. 1 sensor transmits and No. 5 sensor receives
图3. 1号传感器发射、5号传感器接收时的辐角敏感场
3.3. 轨迹提取
考虑到电学全息模型的对称性,将1号传感器设置为发射传感器,考察2~9号传感器作为接收传感器时的辐角敏感场,并据此提取电学全息波传播轨迹,如图4(a)~(h)所示。在特定介质分布下,以上8种轨迹涵盖了这种传感器工作模式下的所有情形。电学全息方法固有的软场效应通过这些传播轨迹得到了充分揭示,且发射、接收传感器之间的劣弧越小,软场效应越为明显。
4. 讨论
4.1. 局限性分析
在本文提出的传感器工作模式下,从辐角敏感场提取电学全息波传播轨迹无疑是有效的。然而,工作模式的变更也可能导致轨迹提取失效。考虑文献 [6] 等提出的一种工作模式。仍然以1号传感器发射、
 (a)
(a) 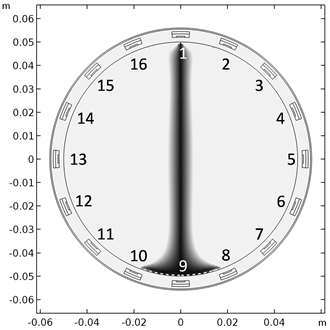 (b)
(b)
Figure 5. Propagating traces of electric holographic wave when No. 1 sensor transmits and No. 5, 9 sensors receive under the previous sensor working condition. (a) No. 5 sensor as the receiving sensor; (b) No. 9 sensor as the receiving sensor
图5. 以往传感器工作模式下1号传感器发射、5号、9号传感器接收时的电学全息波传播轨迹。(a) 5号传感器接收;(b) 9号传感器接收
5号传感器接收为例,此时与发射传感器相邻的16号、2号传感器发射与1号传感器具有相同参数的电学全息波,作为聚焦传感器,与接收传感器相邻的4号、6号传感器作为接地传感器,也在一定程度上起到聚焦的作用。在这种工作模式下,5号、9号传感器接收时的电学全息波传播轨迹分别如图5(a)、图5(b)所示。分别与图4(d)、图4(f)进行对比可知,聚焦传感器和接地传感器的存在,虽然起到了场强增益的作用,但也使得电学全息波传播轨迹发生了偏离,可能会使实际的电学全息过程产生偏差。
4.2. 一种可能的解决方案
文献 [8] 讨论了传感器不一致性对电学全息过程的影响,表明当聚焦传感器发射幅度降低为发射传感器的50%时,电学全息数据区分度有轻度减弱,而接地传感器失效则会带来严重的数据突变。据此,尝试将聚焦传感器发射幅度调节为发射传感器的90%,并将接地传感器工作模式修正为与本文图2一致,重新提取电学全息波传播轨迹,如图6所示。将图6与图4(d)进行对比,发现二者似乎无明显差异。事实上,本节提出的解决方案对章节2.2提出的传感器工作模式起到了一定的场强增益作用。
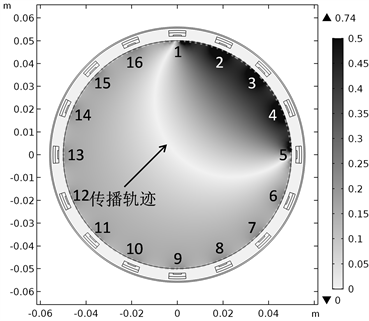
Figure 6. Propagating traces of electric holographic wave when No. 1 sensor transmits and No. 5 sensor receives after applying a solution
图6. 实施解决方案后,1号传感器发射、5号传感器接收时的电学全息波传播轨迹
5. 结论与引申
(1) 在发射传感器单一、接收传感器接收和接地功能合一的工作模式下,辐角敏感场能够用于提取具有软场效应的电学全息波传播轨迹。
(2) 采用多传感器发射模式时,对发射传感器参数进行微调,依然有望得到准确可靠的电学全息波传播轨迹。
(3) 毋庸置疑,采用辐角敏感场提取电学全息波传播轨迹的思想对非均匀介质分布下的电学全息过程依然适用。