1. 引言
旅行商问题(Travelling salesman problem,简称TSP),是由Dantzig等人在1959年提出,给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短路程。旅行商问题在运筹学中非常重要,也是组合优化中的一个NP难问题,在物流、旅游业中有很高的研究价值 [1]。通过对参考文献进行阅读、分析发现,求解TSP问题,最常用的算法是遗传算法和分支定界法 [2] [3] [4]。因此本文选用遗传算法和分支定界法两种算法求解该问题。
2. 问题描述
如图1所示,以位置为0,0的点为起点和终点对这76个点进行遍历。要求找到一条路径使机器人总运行时间最短。已知信息为:机器人最大运行速度1 m/s;在每一点的停留时间与通过速度;以及每一点的坐标。
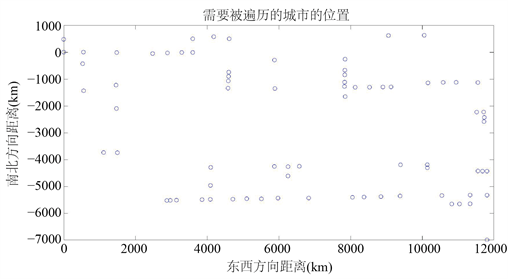
Figure 1. The distribution of cities in TSP
图1. TSP问题城市分布图
忽略机器人的启动与刹车的加速时间,假设机器人全程运动速度为1 m/s。则该问题的解等价于机器人通过旅行商问题求出的最短路径所需的时间加上机器人在所有点停留的时间。本文使用遗传算法与K均值聚类改进分枝定界法求解该问题。
3. 分支定界法
分支定界法是由Richard M. Karp在20世纪60年代发明,成功求解含有65个城市的旅行商问题,创当时的记录。这种方法不但可以求解纯整数规划,还可以求解混合整数规划问题。分支定界法是一种搜索与迭代的方法,选择不同的分支变量和子问题进行分支。
如图1所示,所需要遍历的点有76个,除去起点后,其全排列有75!种可能性。经过测试,本文所使用的计算机平台(16 G内存,英特尔8代i7处理器)在1 h内最多对14个城市使用分枝定界法进行求解,因此首先要对需要遍历的点进行处理,减少其数量。
假设有一个商人需要去中国,日本,美国,巴西中的几个城市送货,且这个商人希望能以最小的路程送完所有的货物。那这个商人必定在当前国家遍历完所有需要前往的城市后才会前往下一个国家。在两个国家之间的城市多次往返的路线不可能是最优解。因此在点分布不均匀的情况下,对分布密集的一些点进行合并可以减少问题的复杂度。其在本质上是排除了一些路线,其中大部分是路程非常长的路线。
本文使用聚类分析对实现对点的合并。聚类分析起源于分类学,由于人们有时难以仅凭借经验和专业知识去对事物进行分类,因此人们把数学工具引用到了分类学中并形成了数值分类学。之后随着多元分析技术的发展,人们又发展出了聚类分析。从分类指标上可以分为划分法,层次法,基于模型的方法,基于网格的方法,基于密度的方法。使用K均值聚类将所有的点划分为指定的类数。K均值聚类的算法需要输入分类数量K,利用各类别中对象的均值更新聚类相似度来完成分类。其流程如下:
1. 从n个数据对象任意选择K个对象作为初始聚类中心。
2. 计算每个对象与聚类中心的距离;并根据最小距离重新对相应对象进行划分。
3. 重新计算每个聚类的均值作为新的聚类中心。
4. 循环2到3直到每个聚类不再发生变化为止。
对图1中76个点进行聚类分析,结果如图2~7下所示:
由上图所示,随着分类类别增加,分类结果越来越精细,成行成列以及距离相对较近的点被很好地划分进了同一类别。且各个类别内点的数量没有超过14个。求取聚类后的各类别的中心点作为各个类别的代表。将其输入到分支定界法中搜索最优路径。
分支定界算法是一种始终围绕着一颗搜索树进行的算法。其将出发点看作搜索树的根节点,从这里出发,分支的含义就是将大的问题分割成小的问题。而定界就是在分支的过程中检查子问题的上下界,如果子问题不能产生一比当前最优解还要优的解,那么砍掉这一支。直到所有子问题都不能产生一个更优的解时,算法结束 [5]。算法流程如下图所示:
由图8所示,我们按顺序遍历每一种排列,并不断更新最小距离,当其中一个父节点的当前距离已经大于最小距离时就跳过该父节点。直到遍历完所有可行解后输出最优解。
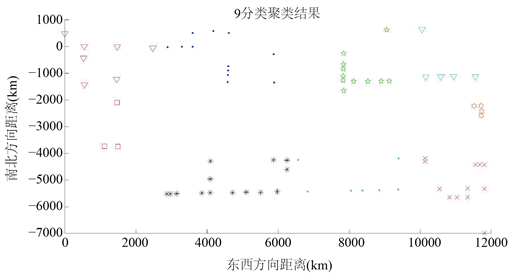
Figure 2. The result of the first classification
图2. 分类结果1
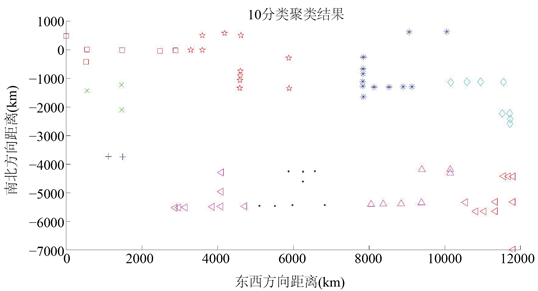
Figure 3. The result of the second classification
图3. 分类结果2
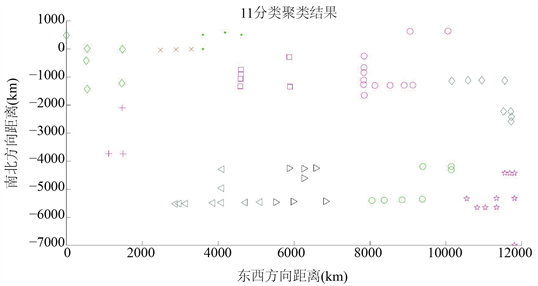
Figure 4. The result of the third classification
图4. 分类结果3
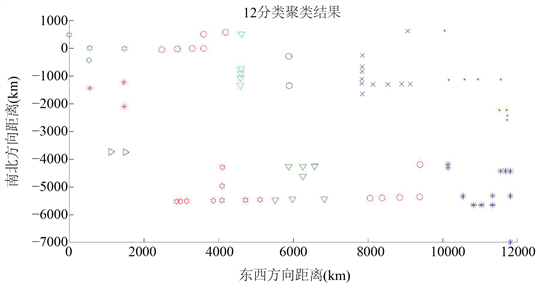
Figure 5. The result of the forth classification
图5. 分类结果4

Figure 6. The result of the fifth classification
图6. 分类结果5
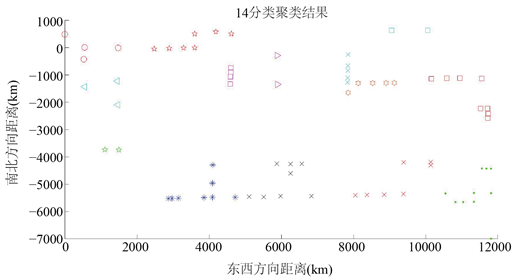
Figure 7. The result of the sixth classification
图7. 分类结果6
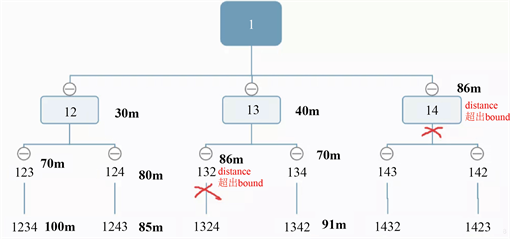
Figure 8. Schematic diagram of branch and bound method
图8. 分支定界法示意图
将各类别的中心点输入到分支定界算法中搜索最优路径便得到了各个集合的最优连接方式。每个集合选出一个在最优路径上下一级集合中心点最近的点作为连接点。然后每个集合分别将上一级的连接点作为起始点,自己的连接点作为终点,其余的点作为需要遍历的点输入到分枝定界法中搜索出最优路径。最后将所有路径合并便得到了一个较优解。
从图9~12可以看出聚类类别数量对整体路径影响不大,只对细微路径有些影响。由于K均值聚类每次随机选取K个点作为起始点,若根据城市分布人工指定起始点可能能进一步减少求解出的最短路程。理论上聚类类别数越多,实际求解过程越接近于直接用分支定界算法进行求解,则求解结果离最优解应该越近。但是经过实验结果表明在聚类类别数量与点的数量差距较大时,增加聚类数量未必能提高解的精度。考虑到求解时间与求解精度,在实际应用该方式时,可以用较少的分类类别数多次运行选取最优解,若能人工指定初始点,该方法的输出将更为稳定。
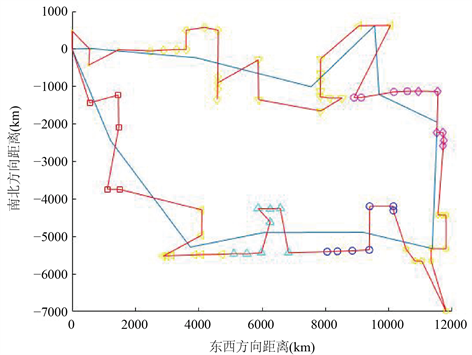
Figure 9. The final path when the number of cluster categories is 11
图9. 聚类类别为11时的最终路径
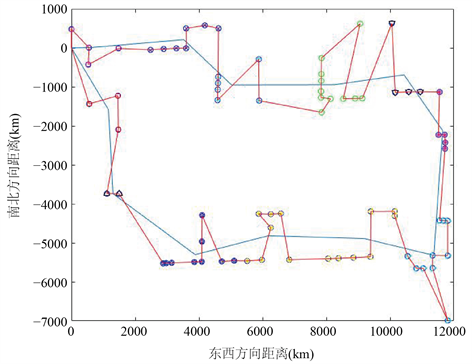
Figure 10. The final path when the number of cluster categories is 12
图10. 聚类类别为12时的最终路径
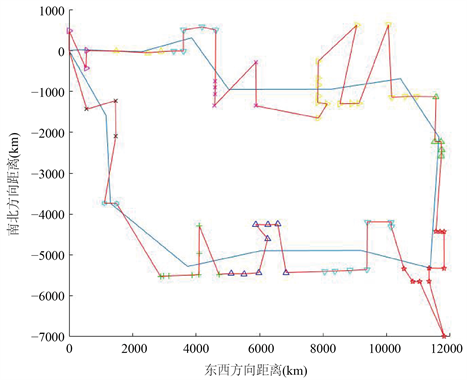
Figure 11. The final path when the number of cluster categories is 13
图11. 聚类类别为13时的最终路径
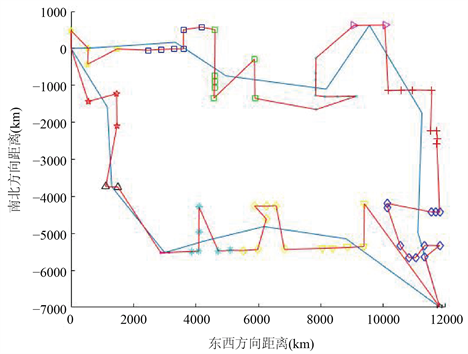
Figure 12. The final path when the number of cluster categories is 14
图12. 聚类类别为14时的最终路径
4. 遗传算法
遗传算法是由John Holland于20世纪70年代根据大自然中生物体进化规律而设计提出的。该算法通过模拟自然进化中选择、交叉、变异现象来搜索最优解,并已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域 [6]。遗传算法流程如图13所示,计算结果如图14所示:
在求解旅行商问题时要对遗传算法的参数编码,适应度函数,交叉方法进行设计,设计结果如下:
1. 将点的遍历顺序作为编码,即编码直接表示路径。
2. 根据每一编码计算其总路程,并用100000/log(总路程 + 1)作为适应度函数。
3. 在两个基因中随机选取两个交叉点,然后根据交叉点选取两个子串直接插入到对方的交叉点中。最后删掉两个后代中各自因交叉产生的重复的点。
设置种群规模为1000;运行次数为5000;淘汰率为30%,交叉概率为90%,变异概率为20%进行搜索,搜索结果如下图所示,最短时间为60381 s。
5. 结论
遗传算法作为一种启发式算法有强的通用性,但是其随机性也很强。经常需要多次运行遗传算法才能得出一个比较理想的结果。同时,随着问题维数的增大,遗传算法需要占用很多的内存来存储基因,计算量也较大。遗传算法搜索结果受参数影响也较大。实际测试中若该问题采用10000种群规模,进化500次,其搜索结果会很差。通过两种算法求解TSP比较,显而易见,基于K均值聚类优化的分枝定界法,在上述问题求解中表现得更好。