一种基于自适应搜索策略的改进萤火虫算法

An Improved Firefly Algorithm Based on Adaptive Search Strategies

摘要: 萤火虫算法(FA)是一种基于群智能的优化技术，它在很多优化问题上表现出较好的性能。然而，它求解复杂优化问题时存在一些问题，如收敛速度慢，精度低。针对这些问题，本文提出了一种新的萤火虫算法(取名AFA)，该方法使用了三种混合策略，以获得好的优化性能。它首先使用一种自适应的参数方法来动态改变步长参数，然后应用一种改进的搜索策略来消除吸引力，于是，AFA不再包含光吸收系数和初始吸引力这2个参数；再使用反向学习来提高解的精度。仿真结果表明，本文提出的AFA算法优化结果优于MFA及PAFA算法。

Abstract: Firefly algorithm (FA) is a recently proposed optimisation technique, based on swarm intelligence, which has shown good optimisation performance. However, FA suffers from slow convergence and low accuracy of solutions. To improve this case, this paper presents a new firefly algorithm (AFA) by using three hybrid strategies to obtain a good optimisation performance. First, an adaptive parameter method is used to dynamically changing the step factor. Second, AFA uses a modified search strategy and eliminates the concept of attractiveness. So, HFA does not include two parameters, ab-sorption coefficient and initial attractiveness. Third, a concept of opposition-based learning is used for improving the accuracy of the global best solution. Experiments on some benchmark problems show that AFA is superior to mimetic FA (MFA) and probabilistic attraction-based FA (PAFA).

1. 标准萤火虫算法

萤火虫算法是由剑桥大学的Yang教授提出的一种群智能算法，它模拟了萤火虫的闪烁求偶行为。类似于粒子群算法，萤火虫算法也是一种基于群体的随机搜索算法。群体中的每个个体(萤火虫)是对应问题的一个候选解。萤火虫算法的搜索依靠个体之间的吸引而产生移动来完成，适应值较好(较亮)的萤火虫具有较大的吸引力，使得适应值较差(较暗)的萤火虫向其移动。

个体(萤火虫)之间的吸引力定义为：

$\beta \left(r_{ij}\right)=\beta {\beta }_0{\text{e}}^{-\gamma r_{ij}^2}$ (1)

其中r_ij表示萤火虫之间的距离，它定义为：

$r_{ij}=\Vert X_i-X_j\Vert =\sqrt{{\displaystyle {\sum }_{d=1}^D{\left(x_{id}-x_{jd}\right)}^2}}$ (2)

对于两个不同的萤火虫X_i和X_j，适应值较差(较暗)的萤火虫将向较好的萤火虫移动。假设X_j优于X_i，则X_i向X_j移动，移动方式表示为：

$x_{id}\left(t+1\right)=x_{id}\left(t\right)+{\beta }_0{\text{e}}^{-\gamma r_{ij}^2}\left(x_{jd}\left(t\right)-x_{id}\left(t\right)\right)+\alpha {\epsilon }_{id}\left(t\right)$ (3)

标准FA中的参数都事先设定的，FA的搜索能力受到其控制参数(如步长因子)的影响，会导致算法收敛早熟；标准FA因参数设置不当而导致算法无法收敛或收敛速度过慢。为了解决这两类问题，使算法具有较好的优化性能，需要对标准FA进行改进。

2. 改进算法的实现

萤火虫算法 [1] [2] 是基于以下三个理想化的特征提出的：(1) 萤火虫不分性别，即萤火虫之间的相互吸引只考虑个体发光的亮度；(2) 吸引力与发光亮度成正比，与个体之间的距离成反比；(3) 萤火虫的亮度由待优化的目标函数值决定，即 $I_i=f\left(x_i\right)$。FA的关键思想是亮度小的萤火虫被亮度大的萤火虫吸引而向其移动，并更新自身的位置。萤火虫的发光亮度取决于自身所处位置的目标值，亮度越高所表示的目标值越好，吸引其他萤火虫的能力也越强。若相邻的个体亮度相同，萤火虫则随机移动。

在标准的FA中，每个萤火虫都能被人群中其他明亮的萤火虫所吸引，这种吸引力机制称为完全吸引模式 [3] [4]，在该模型下，标准FA具有双环操作，因此，计算时间复杂度很高，同时FA的搜索能力受到其控制参数(如步长因子)的影响 [5]。为了解决这个问题，本文提出了一种自适应的参数策略来动态调整步长因子，来消除吸引力。

1) 自适应搜索策略

一些文献指出，FA的搜索能力受到其控制参数(如步长因子)的影响。为了克服这个问题，本文使用了一种自适应的参数策略来动态调整步长因子α的值。

$\alpha \left(t+1\right)={\left(\frac{1}{9000}\right)}^{1/t}\alpha \left(t\right)$ (4)

其中，t指进化的代数。

基于Rao等人提出的Jaya算法，本文针对萤火虫的移动方式进行了下面改进：

$x_{id}\left(t+1\right)=x_{id}\left(t\right)+r_{1d}\left(x_{jd}\left(t\right)-\left|x_{id}\left(t\right)\right|\right)-r_{2d}\left(x_{wd}\left(t\right)-\left|x_{id}\left(t\right)\right|\right)$ (5)

其中，r_1d和r_2d是2个[0,1]之间的随机数，X_w是当前种群中的最差解。与原有的萤火虫移动公式相比，上述改进公式消除了吸引力的概念。因此，我们新提出的算法不再包含初始吸引力和光吸收系数两个参数。

2) 反向学习过程

为了加快算法的收敛，本文使用了反向学习策略(Opposition-Based Learning OBL)。对于当前种群中的最好解X_best，本文利用OBL产生一个反向解 $X_{best}^{*}$。

$X_{best}^{*}\left(t\right)=\bar{a}+\bar{b}-X_{best}\left(t\right)$ (6)

其中， $\left[\bar{a},\bar{b}\right]$ 表示当前种群的搜索区间。如果新产生的反向解 $X_{best}^{*}$ 优于X_best，则使用 $X_{best}^{*}$ 替换X_best。一些研究表明 [6] [7]，反向学习策略OBL有较高的概率找到的反向解比当前解更好。

3) 算法实现过程

Begin

Initialise the population;

while the stopping condition is satisfied do

Update the step factor according to equation (4);

for i = 1 to N do

for j = 1 to N do

if f(Xj) < f(Xi) then

Conduct the movement according to equation (5);

Compute the fitness value of Xi;

end if

end for

Conduct the X_best^* according to equation (6);

ifX_best^* be better than X_best

X_best = X_best^*

end if

end for

end while

End

3. 使用基准函数来测试AFA算法的性能

3.1. 测试函数

为了验证AFA算法性能，本文使用了7个基准函数进行测试 [8] [9] [10] [11]，所有测试函数均为最小值优化函数且全局最优解均为零。

测试函数1：

$\text{F}1\left(X\right)={\displaystyle {\sum }_{i=1}^D{x}_i^2},x_i\in \left[-100,100\right]$ (7)

测试函数2：

$\text{F}2\left(X\right)={\displaystyle {\sum }_{i=1}^D\left|x_i\right|}+{\displaystyle {\prod }_{i=1}^D{x}_i},x_i\in \left[-10,10\right]$ (8)

测试函数3：

$\text{F}3\left(X\right)={\displaystyle {\sum }_{i=1}^D{\left({\displaystyle {\sum }_{j=1}^i{x}_j}\right)}^2},x_i\in \left[-100,100\right]$ (9)

测试函数4：

$\text{F}4\left(X\right)={\max }_i\left(\left|x_i\right|,1\le i\le D\right),x_i\in \left[-100,100\right]$ (10)

测试函数5：

$\text{F}5\left(X\right)={\displaystyle {\sum }_{i=1}^{D-1}\left(100{\left(x_i-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right)},x_i\in \left[-30,30\right]$ (11)

测试函数6：

$\text{F}6\left(X\right)={\displaystyle {\sum }_{i=1}^{D}i{x}_i^4}+rand\left(0,1\right),x_i\in \left[-1.28,1.28\right]$ (12)

测试函数7：

$\text{F}7\left(X\right)=418.9829\cdot D-{\displaystyle {\sum }_{i=1}^{D-1}\left(x_i\sin \left(\sqrt{\left|x_i\right|}\right)\right)},x_i\in \left[-500,500\right]$ (13)

3.2. 测试结果分析

测试实验中上述7个函数维度D分别设置为为10和30，并将AFA的计算结果与MFA和PAFA进行比较，结果显示，本文提出的HFA优于其它两种改进的FA算法。所有算法的终止条件均设置为适应值函数最大个数(MaxFEs)。维度D = 10时，MaxFEs设置为1.0e+04；维度D = 30时，MaxFEs设置为5.0e+04。对于两种不同的维度值，算法的其他参数α，β₀，γ分别设置为0.2，1.0，及1/Γ2。

表1展现了当维度D = 10时，经过30代的演化计算三种算法所得到的最优函数值。从结果来看AFA函数结果除函数F7外均优于MFA。求解函数F7问题时，算法MFA和PAFA的优化结果优于AFA算法的结果。与MFA算法类似的是，AFA算法求解F1至F6函数所表现出的其他性能(收敛速度、不易陷入局部寻优等)亦优于PAFA算法，如对于所有的测试函数求解过程中，当AFA算法已找到最优函数值时，算法MFA和PAFA仍陷入局部寻优过程。正如文章开始提到的“标准FA的搜索能力受到其控制参数(如步长因子)的影响，会导致算法收敛早熟”，通过自适应策略，本文提出的AFA算法不易陷入局部寻优的过程。

表2展现了当维度D = 30时，经过30代的演化计算三种算法所得到的最优函数值。如表所示，AFA求解F1，F2，F3，F5，F6，F7函数展现了较好的算法性能。MFA在求解F4函数时优于AFA。相对于PAFA，求解F1，F2，F5，F6函数时MFA能够找到更加精确地解。求解F3，F4，F7函数时PAFA性能优于AFA。

Table 1. Computational results of each algorithm for D = 10

表1. 维度D = 10各算法寻优结果

Table 2. Computational results of each algorithm for D = 30

表2. 维度D = 30各算法寻优结果

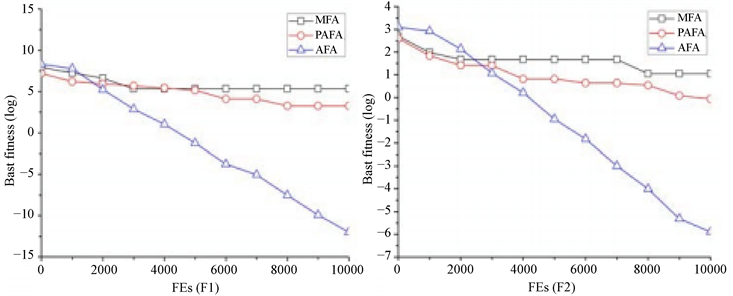
图1展示的是当维度D = 10，算法AFA、MFA和PAFA求解函数F1，F2时的算法收敛过程。

(a) (b)

Figure 1. The search processes of AFA, MFA, and PAFA for D = 10, (a) function F1; (b) function F2

图1. D = 10，AFA、MFA及PAFA的收敛过程，(a) 功能F1，(b) 功能F2

图2展示的是当维度D = 30，算法AFA、MFA和PAFA求解函数F1，F2时的算法收敛过程。

(a) (b)

Figure 2. The search processes of AFA, MFA, and PAFA for D = 30, (a) function F1; (b) function F2

图2. D = 30，AFA、MFA及PAFA的收敛过程，(a) 功能F1，(b) 功能F2

从收敛曲线来看，本文提出AFA的收敛速度也比MFA和PAFA快。通过标准反向学习过程，AFA解决了“FA因参数设置不当而导致算法无法收敛或收敛速度过慢”问题。

测试实验中，MaxFEs的值设置的较小。当维度从10增加到30时，MaxFEs的值从1.0e+04增加到5.0e+04，算法MFA和PAFA的实验结果值得到了改进，但如果将MaxFEs设置为一个更大的值时，AFA可能会有更好的表现。通过实验可以得出，MaxFEs的值对AFA的算法性能影响很大。

4. 结束语

本文提出了一种新的数值优化算法AFA，该算法基于标准的萤火虫算法FA，采用三种改进的措施，包括自适应的参数方法来动态改变步长参数，应用一种改进的搜索策略来消除吸引力；再使用反向学习来提高解的精度。为了验证AFA的算法性能，文章测试了7个标准的数值优化函数，并分别测试了所测7个函数不同维度值。实验结果表明，AFA算法在求解大部分函数时所表现出来的性能都优于算法MFA和PAFA。

然而，通过函数收敛图可以发现，AFA在整个优化过程中，该算法的收敛速度并没有明显优于MFA和PAFA算法，如何解决这一问题，使AFA算法性能更好，这将是作者今后的研究工作之一。

基金项目

本文受到安徽省省级示范实验实训中心项目(2018sxzx38)；2018教育部智融兴教课题(2018A01010)；教育部2019年协同育人项目(201901258002)；安徽省教育厅高校优秀拔尖人才资助项目(gxyqZD2020054)等项目资助。